Прочность обеспечивается.

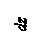
Пример 2.Ломанный брус(рис.6.2,а) круглого поперечного сечения радиусом R = 1 см равномерно вращается вокруг оси АС с угловой скоростью

W = 30 рад · с^-1. Удельный вес материала бруса 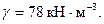Проверить прочность бруса при [ σ] = 100 мПа, l = 25 cм.

Решение

При равномерном вращении бруса с угловой скоростью W центробежные силы инерции постоянны во времени. На участке DЕ они распределены равномерно с интенсивностью

q = ma = mW² r,

где m = 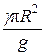- масса единицы длины стержня, а = W² r – центростремительное ускорение, r = l – расстояние от DЕ до оси вращения.

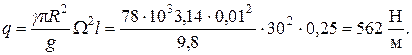
Участок ВD нагружен силами инерции q_z, которые изменяются от нуля до максимума по линейному закону (рис.6.2, б):

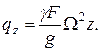
Равнодействующая сил инерции на участке ВD направлена вдоль оси ВD и равна

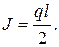
Определим опорные реакции:

Σ М_А =0.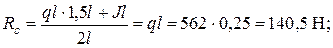

Σ М_c =0.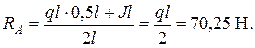

Проверка: Σ Y = 0.

R_А+ R_c – ql - J = 70,25+ 140,5 – 140,5 – 70,25 = 0.

Эпюра изгибающих моментов показана на рис. 6.2,в.

Опасное сечение находится справа от точки В, где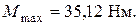

Максимальное напряжение в опасном сечении

.

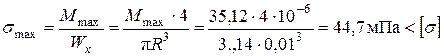Прочность обеспечивается.

3.Расчет конструкций на ударные воздействия

В основе приближенной теории удара, рассматриваемой в курсе сопротивления материалов, лежит гипотеза о том, что эпюра перемещений от груза Р при ударе подобна эпюре перемещений, возникающих от этого же груза, но действующего статически (1).

В случае ,когда масса упругого тела, подвергающегося удару мала, и ее при расчете можно принять равной нулю, гипотеза позволяет получить точное решение задачи. Рассмотрим вначале этот случай.

Три основных вида деформации стержней - осевое растяжение - сжатие, кручение и изгиб определяют и главные разновидности ударных воздействий на деформируемый элемент конструкции: удар осевой или продольный , как динамическая интерпретация осевой деформации; удар при кручении, как следствие резкого торможения и останова вращающихся деталей машин и механизмов; поперечный удар, сопровождающийся деформацией изгиба.

При осевом нагружении (если в статике и при ударе материал работает в пределах закона Гука) можно через один параметр 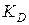- коэффициент динамичности, обозначить три одинаковых соотношения:

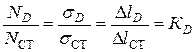
Где 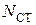, , 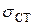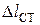- нормальные силы, нормальные напряжения и абсолютные перемещения при статическом нагружении;

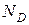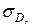
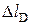, - то же в динамике.

Выражение для 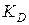можно получить, рассматривая баланс энергий при ударе.

Потенциальная энергия первоначального положения груза при высоте падения h:

.

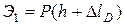Потенциальная энергия , накопленная в сжимаемом ударом стержне:

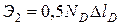
Составляем баланс энергий:

.

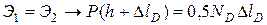Запишем полученное уравнение с привлечением коэффициента динамичности и значения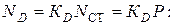

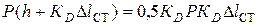
Сведя полученное уравнение к алгебраическому уравнению 2-го порядка относительно 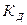и решая его, из двух формально возможных корней этого уравнения берем один, который и определяет расчетную формулу для коэффициента динамичности при продольном ударе:

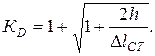
Полученная формула в случае h = 0 — падение груза с нулевой высоты, дает 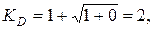что отражает парадоксальный на первый взгляд результат действия внезапно приложенной динамической нагрузки.

Во всех других вариантах (кроме h = 0), когда высота падения груза существенно больше 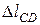, формулу для 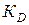часто используют в более простом виде:

.

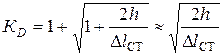Пример 6.3.Образец из цементного камня высотой l = 4 см поперечным сечением F = 1 см² подвергается воздействию груза Р = 10 Н, падающего с высоты 20 см (рис. 6.3). Выяснить, какой толщины 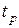требуется амортизирующая резиновая прокладка для того, чтобы 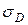в образце не превышали по модулю 2 МПа. В расчетах принять 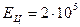мПа,

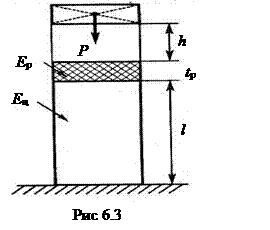
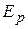= 1 мПа.

Решение.

Подсчитываем сначала статические напряжения:

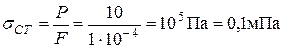
Следовательно, коэффициент динамичности системы должен отвечать условию:

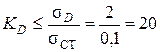
Это позволяет найти предельное значение для :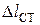

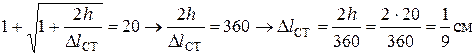
При наличии амортизатора толщиной 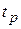статическая деформация состоит из двух частей, связанных с деформацией цементного образца и резины:

;

.

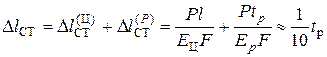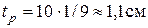Толщина амортизатора должна быть не меньше 1,1 см.

Пример 6.4. На стальной ступенчатый стержень (рис. 6.4,а) с высоты h падает груз массой т.

Определить максимальные напряжения в стержне. Как изменятся максимальные напряжения, если в верхней части стержня высверлить отверстие глубиной 2,8 l (рис.6.4,б). Диаметр отверстия выбран таким образом, чтобы площадь ослабленного сечения в верхней части была равна F₁.

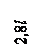
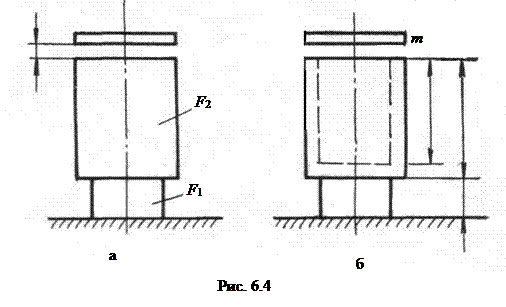т = 40кг; h=0,02 м; F₁ = 5 см²; F₂=10 см²; l = 0,1 м.

Решение.

Вес груза G = mg = 40×9,8 = 392 H. Максимальные стати­ческие (сжимающие) напряжения возникают в нижней части стержня:

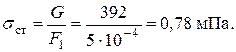
Статическое перемещение в месте удара равно укорочению стержня при статическом приложении груза G:

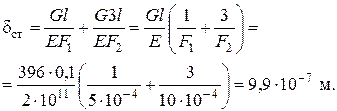
Коэффициент динамичности:

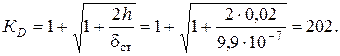
Динамическое напряжение:

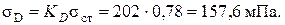
Если в верхней части стержня высверлить отверстие, максимальные статические напряжения не изменятся, а статическое перемещение верха стержня будет равно:

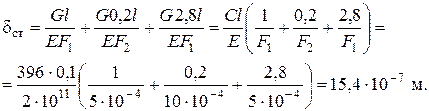
Коэффициент динамичности:

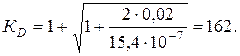
Динамические напряжения:

s_D = 162×0,78 = 126,3 мПа.

Снижение напряжений составило:

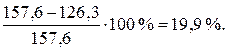
Формула, полученная для коэффициента динамичности при продольном ударе, может быть успешно использована и в случае плоского поперечного изгиба в виде:

,

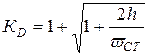где 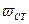- прогиб балки в том сечении, где на нее падает груз.

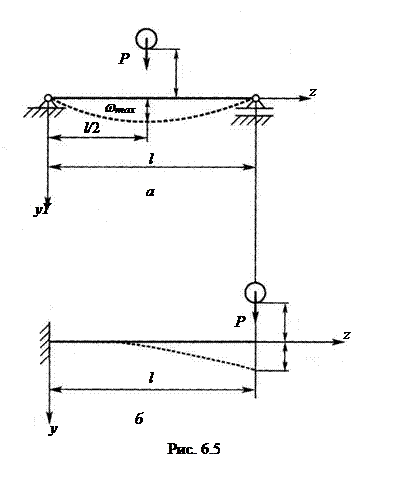
Применительно к балке на двух опорах, на которую груз падает посередине (рис. 6.5, а), для подсчета 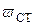можно использовать известный «табличный» результат:

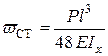
Максимальные динамические нормальные напряжения и прогибы также возникают в середине пролета балки и подсчитываются так:

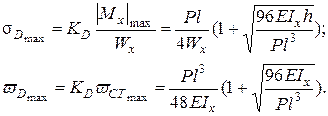
Для консоли, на которую груз падает в крайнем торцевом сечении (рис. 6.5, б), статический прогиб в этом сечении также определяется известной формулой:

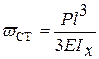
Здесь же возникают максимальные прогибы динамические, а наибольшие нормальные напряжения будут в заделке:

;

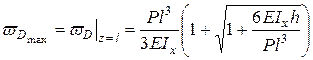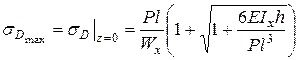
Пример 6.5.Груз массой 200 кг падает с высоты h = 10 см на середину пролета KL двутавровой балки №20 (рис. 6,6). Определить максимальные динамические напряжения, возникающие в балке и сравнить их с вариантом, когда в шарнире «К» установлена жесткая опора (рис 6.6, б). В расчетах принять: E= 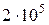мПа, а = 1 м.

Решение.

	Рис 6.6

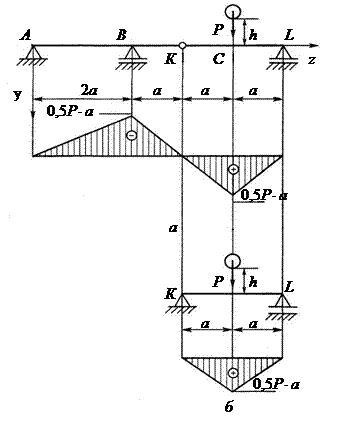
Необходимые для расчета геометрические характеристики двутавра №20 принимаем из сортамента: 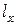= 1840 см, 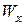= 184 см. Вес груза

Р = mg = 200 × 9.8 = 1 960 Н.

Статический прогиб в точке падения груза Р определяем, интегрируя приближенное дифференциальное уравнение изогнутой оси с учетом шарнира в точке К. В результате расчетов имеем: 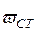= 0,221 мм. Находим коэффициент динамичности:

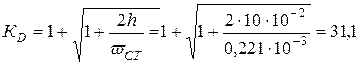
По максимальным нормальным напряжениям равноопасными оказываются сечения «В» и «С». Здесь 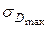определяется так:

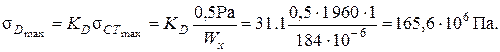
Если же вместо схемы «а» рис. 6.6 мы перейдем на вариант жесткой опоры в сечении «K» (рис. 6.6, б), изменится величина :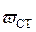

.

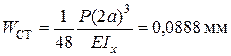Соответственно, динамический коэффициент: 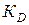= 48,5. А максимальные динамические напряжения в сечении «с» 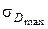= 258 мПа.

Если [σ] = 160 мПа, то в схеме «а» можно считать, что с перегрузом в 3.5% конструкция пригодна к эксплуатации; во втором варианте эксплуатация балки недопустима.

Наиболее типичным вариантом удара при деформации кручения является случай резкого торможения или внезапного останова вращающихся деталей машин и механизмов. В этом случае целесообразно определять динамические касательные напряжения прямо через энергию вращающихся тел.

Пример 6.6. Вал маховика, равномерно вращается с угловой скоростью W (рис. 6.7). Торможение вала происходит в сечении «А» на расстоянии l от маховика. Получить выражения для подсчета максимальных касательных напряжений при кручении вала кругового сечения радиусом r.

Решение

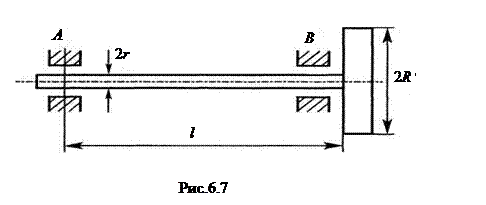
Если не учитывать потери при торможении, кинетическая энергия маховика (Э) переходит в потенциальную энергию деформации вала ( 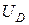). Каждая из этих величин определяется по известным формулам:

;

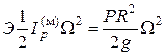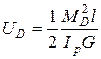
где 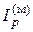— полярный момент инерции массы маховика ; 2R — диаметр маховика; Р — вес маховика.

Максимальные касательные напряжения :

.

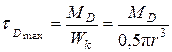Потенциальную энергию, накапливаемую валом при этом, можно выразить через напряжения:

,

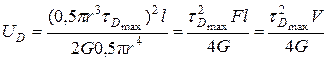где V=Fl — объем деформируемого тела, в данном случае вала.

В итоге из баланса энергий удается получить формулу для динамических касательных напряжений:

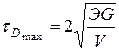
Важно заметить, что формула для коэффициента динамичности системы практически работает для любого варианта деформации, в том числе и сложной. Важно только правильно определить статические перемещения по направлению действия падающего груза в точке соприкосновения груза с элементом конструкции. Далее все динамические силовые и деформационные характеристики системы получаются путем умножения внутренних усилий, напряжений и перемещений, найденных в статике, на коэффициент динамичности системы. Это лишний раз подчеркивает необходимость знания статического расчета любой деформируемой системы.

При расчете на удар упругих систем, масса которых сопоставима с массой падающего груза, вначале рассматривается случай, когда система несет сосредоточенную массу Q/g, расположенную в месте падения груза весом Р (1). Составляя баланс энергий, нетрудно получить выражение коэффициента динамичности, учитывающее заданное соотношение веса сосредоточенной массы и падающего груза:

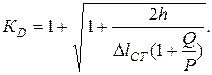
Если удар совершается на систему с равномерно распределенной по ее длине массой , в выражение коэффициента динамичности К_D вводится коэффициент b приведения распределенной массы к условно сосредоточенной в месте падение груза (1):

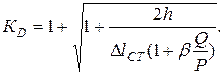
В учебной литературе можно найти значения коэффициента b для частных случаев рассматриваемой задачи . Так например, при продольном ударе груза, вызывающем деформацию сжатия ( или растяжения) бруса постоянного сечения b=1/3 , а при изгибающем ударе посередине балки, лежащей на двух опорах, b = 17/35.

Для определения вызванных ударом наибольших динамических напряжений и перемещений с учетом массы упругой системы, так же как и при расчете без учета массы, напряжения и перемещения, найденные путем расчета системы на статическое действие силы Р, следует умножить на коэффициент динамичности К_D, Прибавив к найденным значениям, напряжения и деформации от собственного веса упругой системы (если по условию задачи их следует учитывать),получим полные напряжения и перемещения ,возникающие при ударе.

4. Напряжения и деформации при колебаниях.

При колебаниях системы с сосредоточенными массами возникают силы инерции; с ними связаны дополнительные напряжения и деформации, которые должны учитываться в расчетах.

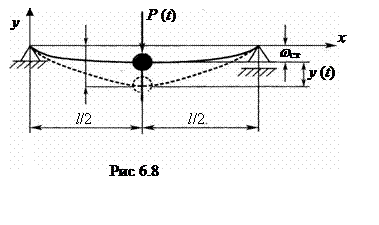
Для вывода уравнений колебаний на основании принципа Даламбера рассматривается равновесие системы с учетом сил инерции. На примере поперечных колебаний стержня на двух опорах с сосредоточенной в пролете массой m (рис 6.8) .

Для упругой системы с одной степенью свободы уравнение имеет вид:

,

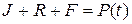где 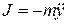- сила инерции;

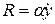- сила сопротивления движению системы, для случая вязкого трения принимаемая пропорциональной скорости ( 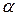-коэффициент пропорциональности);

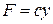--сила упругости, определяемая с учетом жесткости системы с.

При действии гармонической возмущающей силы 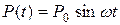, приходим к уравнению

,

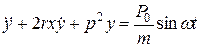где обозначено:

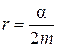- параметр затухания колебаний;

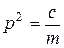- квадрат частоты собственных колебаний системы.

Общее решение полученного уравнения имеет вид:

,

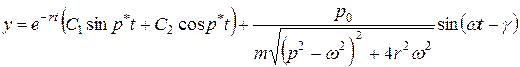где С₁ и С₂ определяются из начальных условий, 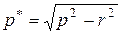- частота затухающих колебаний системы, а угол 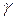характеризует отставание фазы перемещений от фазы силы и определяется выражением

.

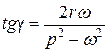Амплитуда установившихся колебаний

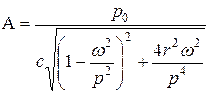
Отношение амплитуды А к статическому перемещению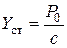

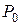( - амплитудное значение возмущающей силы) равно

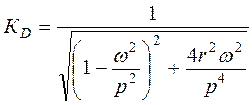
и представляет собой коэффициент динамичности.

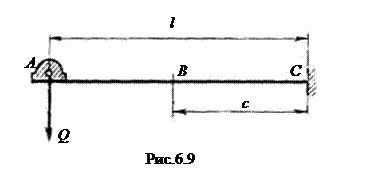
Пример 6.7. На конце консольной балки (рис.6.9) длиной l = 1 м находится двигатель весом Q = 1,23 кН. Балка — стальной двутавр № 8 (Е=21×10⁴ МПа; J = 78×10⁸ м⁴). Собственным весом балки по сравнению с весом двигателя пренебречь. Определить частоту и период собственных колебаний.

Решение.

Прогиб конца консоли от собственного веса двигателя:

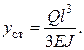
Частота колебаний:

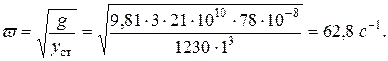
Период:

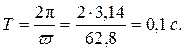
Число колебаний в минуту f_т = 60/Т = 600.

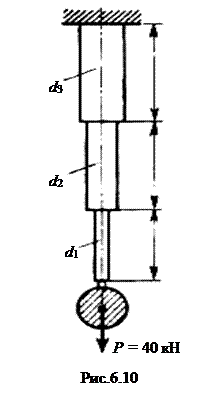
Пример. 6.8. Определить число свободных продольных колебаний в минуту стержня переменного сечения, нагруженного на нижнем конце силой Р = 40 кН (рис. 6.10).Весом стержня пренебречь. Данные: d₁ =2 см; d₂ = 3 см; d₃ = 4 см; Е = 20×10⁴ мПа; l₁ = 50 см; l₂ = 70 см; l₃ = 100 см.

Решение

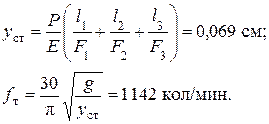
Пример 6.9. При работе двигателя массой m=400 кг из-за неуравновешенности вращающихся частей возникает возмущающая сила P₀ = 0,5 кН. Мотор делает 1000 оборотов в минуту. Проверить прочность рамы (рис. 6.11) в резонансном режиме, пренебрегая собственной массой элементов рамы и приняв коэффициент затухания колебаний 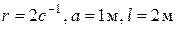. Рама изготовлена из двутавра №30; , .

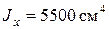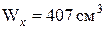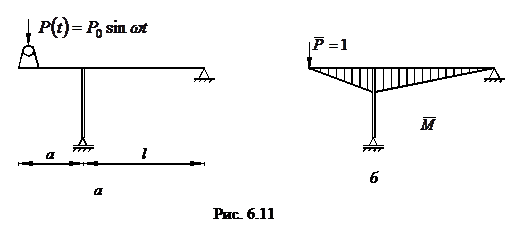Решение

Коэффициент жесткости системы определяется соотношением 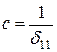, где 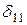- перемещение точки приложения массы от единичной силы. Величину 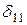вычислим по формуле Мора с использованием приема Верещагина. Единичная эпюра представлена на рис. 6.11,б.

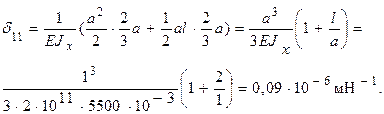
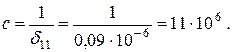
Частота собственных колебаний

.

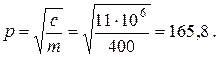Частота вынужденных колебаний:

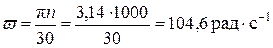
Коэффициент динамичности

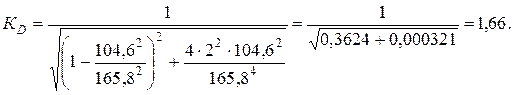
Следует отметить, что учет затухания колебаний в данном случае практически не сказывается на результате расчета (второе слагаемые под корнем значительно меньше первого).

Наибольшее нормальное напряжение, возникающее от веса двигателя в опасном сечении рамы

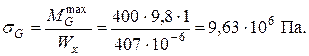
Наибольшие нормальные напряжения в том же сечении от действия возмущающей силы

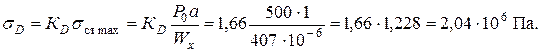
Динамические напряжения изменяются во времени по симметричному циклу. Суммарные максимальные напряжения в опасных точках расчетного сечения

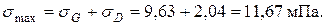
В резонансном режиме имеет место приближенное равенство частот

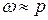
Динамический коэффициент при резонансе

.

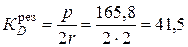Соответствующие максимальные напряжения

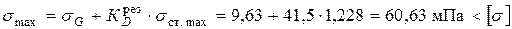
прочность обеспечивается.

Вопросы и задания для самоконтроля

1. Какие основные виды ударных воздействий на стержень Вам известны?

2. Что такое «коэффициент динамичности»?

3. Как влияет деформируемость, податливость системы под воздействием статических нагрузок на величину коэффициента динамичности?

4. Что означает термин «внезапно приложенная нагрузка»? Чему при этом равен коэффициент динамичности?

5. В каком стержне, стальном или алюминиевом, при всех прочих равных условиях коэффициент динамичности при ударе будет выше?

6. Как влияет на величину коэффициента динамичности учет веса деформируемого тела?

7. За счет чего амортизирующие устройства в системе снижают коэффициент динамичности?

8. Совпадает ли при поперечном ударе сечение, на которое падает груз, с сечениями, в которых действуют максимальные ударные напряжения и возникают максимальные прогибы балки?

9. Как Вы понимаете выражение «вынужденные поперечные колебания стержня с одной степенью свободы»?

10.Какие основные силы принимаются в расчет при выводе уравнения движения вынужденных колебаний стержня?

11.От чего главным образом зависит величина коэффициента нарастания амплитуды вынужденных колебаний системы?

12.Какие Вам видятся основные способы, приемы снижения коэффициента динамичности системы в условиях вынужденных колебаний?