Линейные системы. Условие квазистационарности

Пусть L – характерные размеры системы (электрической цепи), c – скорость света, Т – характерное время наблюдения или измерения сигнала. Для периодического сигнала Т = 1/f, где f – частота. Тогда можно сформулировать условие квазистационарности:

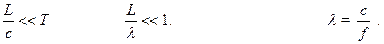
или Здесь длина волны (2.1)

Если выполнено условие квазистационарности, то можно обоснованно считать, что электромагнитное поле во всех частях нашей системы меняется синхронно, а напряжения и токи синфазны.

Если выполняется обратное неравенство: λ < L , (2.2)

то такие системы называются распределёнными.

Приведём пример: частоте переменного тока в сети f = 50 Гц соответствует длина волны λ ~ 6000 км. Диаметр Петербурга (~ 30 км) – значительно меньше. И для области от Петербурга до Москвы (~ 600 км) условие квазистационарности (2.1) тоже выполнено.

Другой пример: частоте f = 1800 МГц (рабочий диапазон мобильного телефона) соответствует длина волны λ ~ 17 см. В этом случае размеры приёмника могут оказаться сравнимыми с длиной волны и условие квазистационарности (2.1) может быть не выполнено (или выполнено без запаса).

Линейность.Условие линейности можно сформулировать следующим образом:

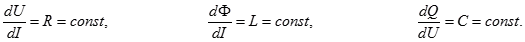
(2.3) (2.4) (2.5)

В этом случае отклик линейно пропорционален воздействию. Например, ток I пропорционален напряжению U: I = U/R, поток Ф пропорционален току I: Ф = L I.

Физически ясно, условия (2.3 – 2.5) справедливы при малых I, U, Q, Ф. В обратном случае различные нелинейные эффекты нарушат эту связь. Следует подчеркнуть, что малость в каждом случае требует отдельного анализа.

Например, на рис. 2.1 приведена типичная вольтамперная характеристика (ВАХ) туннельного диода. Видно, что условие линейности выполняется для него при токах I < 0.8 мА и ещё на двух небольших участках характеристики.

Рис. 2.1. Вольтамперная характеристика туннельного диода 1И104.

Сосредоточенные линейные элементы.При прохождении тока по цепи возможно существование участков, в которых падение напряжения по-разному связано с протекающим током. Если выполнено условие квазистационарности, то можно пользоваться понятиями идеальных сосредоточенных элементов: сопротивление R, ёмкость C и индуктивность L – см. рис. 2.2.

Рис. 2.2. Графические обозначения идеальных сосредоточенных элементов: сопротивления R,

ёмкости C и индуктивности L и простейшие модели, учитывающие паразитные эффекты в сосредоточенных элементах.

В действительности, при прохождении тока через реальные конденсаторы, и резисторы, и катушки индуктивности проявляется ряд паразитных эффектов. Например, у катушки индуктивности может быть заметное омическое сопротивление, а у конденсатора – индуктивность и сопротивление утечки. Эти эффекты могут быть учтены в простейших моделях, примеры которых приводятся на рис. 2.2. В нашем курсе мы будем пренебрегать паразитными эффектами.

Пусть условия квазистационарности и линейности выполнены, и можно пользоваться моделями сосредоточенных элементов. В этом разделе мы напомним их свойства.

Рис. 2.3.

Для резистора с сопротивлением R имеем: U_R = I_R R, [R] = Ом;

проводимость G = 1/R, [G] = Сименс. Здесь I_R – ток, текущий через резистор, U_R – напряжение на нём.

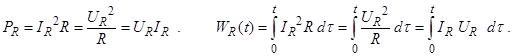(2.6)

P_R – тепловая мощность, W_R – тепловая энергия, выделяющаяся на резисторе.

Рис. 2.4.

Для конденсатора с ёмкостью С имеем:

Q_C = С U_C, [С] = Ф (Фарада или Фарад).

Здесь Q_C , U_C – заряд и напряжение на конденсаторе,
а I_C – ток зарядки – разрядки.

W_C – изменение энергии конденсатора. (2.7)

Рис. 2.5.

Для катушки индуктивности L имеем:

Φ = L I_L , [L] = Гн (Генри). U_L = dΦ/dt = L dI_L/dt .

(2.8)

Здесь Φ, I_L и U_L – соответственно магнитный поток, ток и напряжение на катушке индуктивности, W_L – изменение энергии катушки индуктивности.

Как правило, на радиотехническом жаргоне, резисторы и катушки индуктивности называют сопротивлениями и индуктивностями, а конденсаторы называют ёмкостями реже.