Передаточная функция, коэффициент передачи, временные и частотные характеристики
Работу линейного устройства определяют два вида характеристик – временные и частотные.
Передаточная функция устройства K(p), позволяющая найти временные характеристики определяется согласно преобразованию Лапласа.
Согласно преобразованию Фурье определяется коэффициент передачи K(jω), определяющий частотные свойства объекта.
МеждуK(p)и K(jω) существует прямая связь, позволяющая от временных характеристик перейти к частотным и обратно.
Элементарным звеном линейной системы является четырехполюсник (рис. 6.31).
Рис.6.31 Четырехполюсник
Свойства линейного четырехполюсника можно описать с помощью линейного дифференциального уравнения n-й степени:
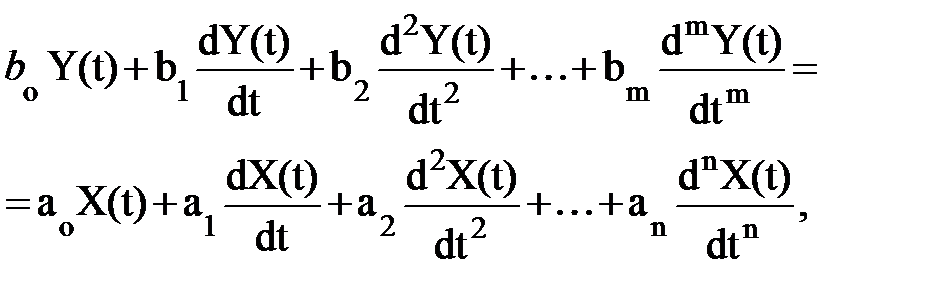
где X(t) – входной сигнал, а Y(t) – выходной.
Согласно преобразованию Лапласа-Карсона:
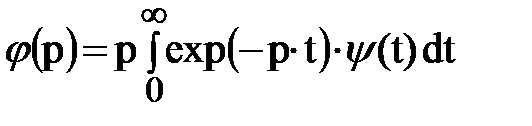
где φ(p) – изображение оригинала ψ(t) (значение ψ(t)=0 при t<0).
Уравнение (1) можно записать в операционной форме:
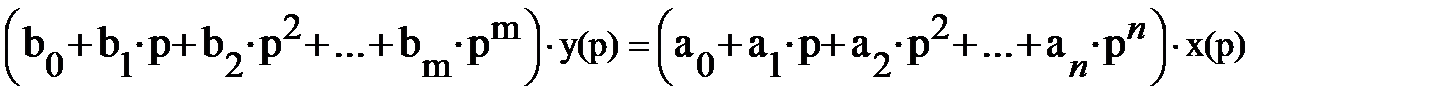
из которой получим передаточную функцию устройства:
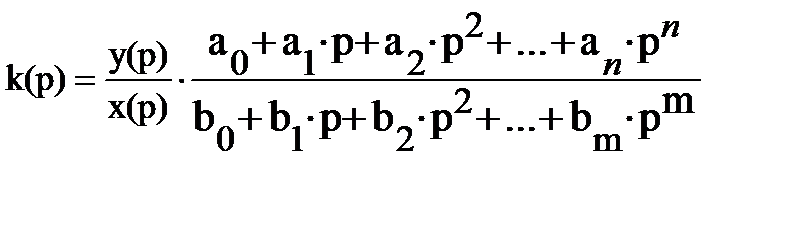
или при разложении числителя и знаменателя на множители (n≤m):
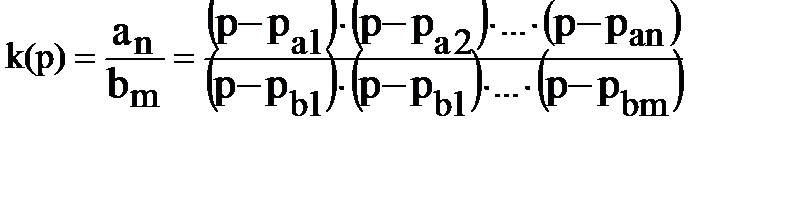
где pa1, pa2, pan – корни уравнения 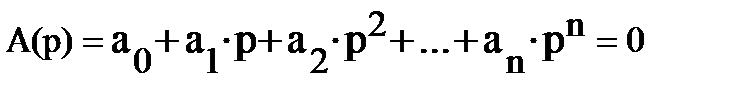 , называемые нулями передаточной функции K(p);
, называемые нулями передаточной функции K(p);
pb1, pb2, pbm - корни уравнения 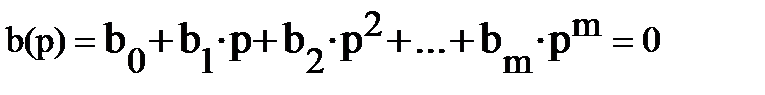 , называемые полюсами передаточной функции K(p).
, называемые полюсами передаточной функции K(p).
В устойчивой системе все полюсы оператора K(p) располагаются в левой полуплоскости комплексного переменного:
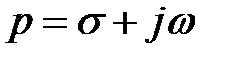
т.е. действительные части всех полюсов
Re(pbk)<0, где k=0,1,2….m
6.6.2 Коэффициент передачи K(jω)
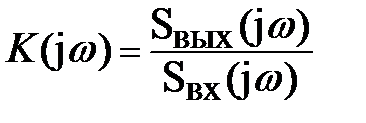 ,
,
где 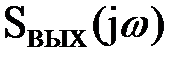 и
и 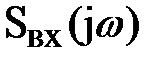 – спектральные плотности выходного и входного сигнала (определяются как преобразование Фурье от Y(t) и X(t)).
– спектральные плотности выходного и входного сигнала (определяются как преобразование Фурье от Y(t) и X(t)).
Учитывая, что интеграл Фурье есть частный случай преобразования Лапласа при p=jω из передаточной функции путем подстановки получим комплексный коэффициент передачи устройства:
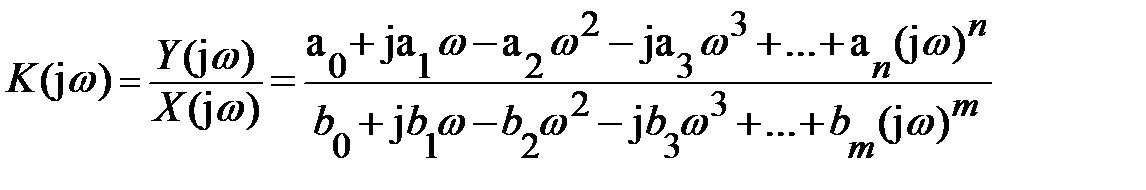
Это выражение можно представить в виде:
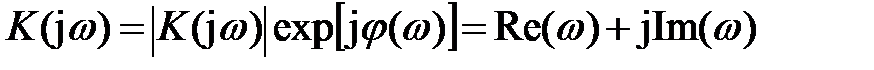 ,
,
где модуль и фазу коэффициента передачи можно выразить через действительную и мнимую части комплексного числа:
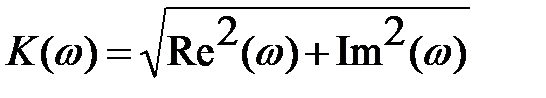 ,
,
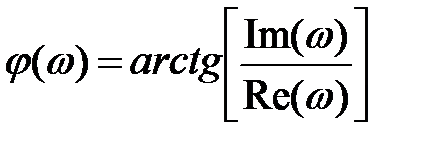
С помощью приведенных выражений можно определить частотные и временные характеристики линейного устройства.
Дата добавления: 2017-05-02; просмотров: 4434;











