Емкости p-n перехода
Изменение внешнего напряжения dU на p-n переходе приводит к изменению накопленного в нем заряда dQ. Поэтому p-n переход ведет себя подобно конденсатору, емкость которого С = dQ/ dU.
В зависимости от физической природы изменяющегося заряда различают емкости барьерную (зарядную) и диффузионную.
Барьерная (зарядная) емкость определяется изменением нескомпенсированного заряда ионов при изменении ширины запирающего слоя под воздействием внешнего обратного напряжения. Поэтому идеальный электронно-дырочный переход можно рассматривать как плоский конденсатор, емкость которого определяется соотношением
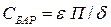 , (1.41)
, (1.41)
где П, d - соответственно площадь и толщина p-n перехода.
Из соотношений (1.41) и (1.31) следует
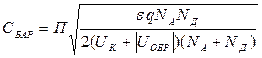 .
.
В общем случае зависимость зарядной емкости от приложенного к p-n переходу обратного напряжения выражается формулой
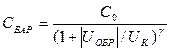 ,
,
где C0 — емкость p-n перехода при UОБР = 0; g - коэффициент, зависящий от типа p-n перехода (для резких p-n переходов g = 1/2, а для плавных g = 1/3).
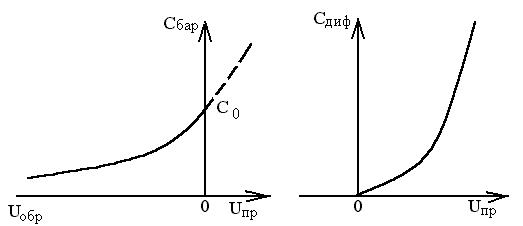
Барьерная емкость увеличивается с ростом NА и NД, а также с уменьшением обратного напряжения. Характер зависимости СБАР = f(UОБР) показан на рис. 1.13,а.
Рассмотрим диффузионную емкость. При увеличении внешнего напряжения, приложенного к p-n переходу в прямом направлении, растет концентрация инжектированных носителей вблизи границ перехода, что приводит к изменению количества заряда, обусловленного неосновными носителями в p- и n-областях. Это можно рассматривать как проявление некоторой емкости. Поскольку она зависит от изменения диффузионной составляющей тока, ее называют диффузионной. Диффузионная емкость представляет собой отношение приращения инжекционного заряда dQинж к вызвавшему его изменению напряжения dUпр, т. е. 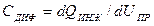 . Воспользовавшись уравнением (1.30), можно определить заряд инжектированных носителей, например дырок в n-области:
. Воспользовавшись уравнением (1.30), можно определить заряд инжектированных носителей, например дырок в n-области:
.
| а) | б) |
Рисунок 1.13 Зависимость барьерной (а) и диффузионной (б) емкостей p-n перехода от напряжения.
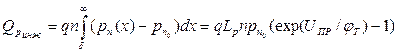 .
.
Тогда диффузионная емкость, обусловленная изменением общего заряда неравновесных дырок в n-области, определится по формуле
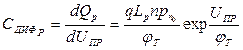 .
.
Аналогично для диффузионной емкости, обусловленной инжекцией электронов в p-область,
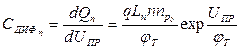 .
.
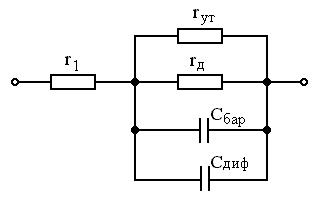
Рисунок 1.13 Эквивалентная схема p-n перехода.
Общая диффузионная емкость
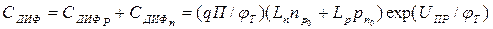 .
.
Зависимость ёмкости от прямого напряжения на p-n переходе показана на рисунке 1.13, б.
Полная емкость p-n перехода определяется суммой зарядной и диффузионной емкостей:
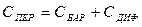 .
.
При включении p-n перехода в прямом направлении преобладает диффузионная емкость, а при включении в обратном направлении - зарядная.
На рис. 1.14 приведена эквивалентная схема p-n перехода по переменному току. Схема содержит дифференциальное сопротивление p-n перехода rД, диффузионную емкость СДИФ, барьерную емкость СБАР и сопротивление объема p- и n-областей r1. На основании уравнения (1.37) можно записать:
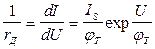 .
.
Если при прямом включении p-n перехода Uпр >> jт, то:
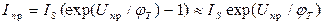 ;
; 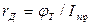 .
.
При комнатной температуре 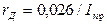 ; (1.42)
; (1.42)
(в соотношении (1.42) значение тока подставляется в амперах). Сопротивление утечки rУТ учитывает возможность прохождения тока по поверхности кристалла из-за несовершенства его структуры. При прямом включении p-n перехода СБАР << СДИФ, дифференциальное сопротивление rД ПР мало и соизмеримо с r1, поэтому эквивалентная схема принимает вид, показанный на рис. 1.15, а.
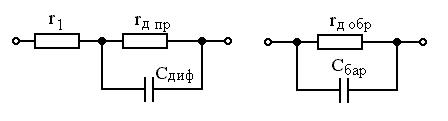
| а) | б) |
Рисунок 1.15 Упрощенные эквивалентные схемы p-n перехода.
При обратном смещении rД ОБР >> r1, СБАР >> СДИФ и эквивалентная схема имеет вид, показанный на рис. 1.15, б.
Дата добавления: 2017-05-02; просмотров: 1569;











