Деформации и напряжения в паяных соединениях и узлах

В зависимости от величины, знака и характера распределения остаточных (внутренних) и приложенных (внешних) напряжений прочность спая может увеличиваться или уменьшаться. Прежде чем рассчитывать прочность конструкции, необходимо правильно определить вид напряженного состояния, в котором она будет находиться в процессе эксплуатации.

Существуют четыре основных источника образования остаточных деформаций и напряжений в паяных соединениях [2]: 1) термические напряжения, возникающие вследствие неравномерного нагрева и охлаждения паяных деталей и конструкций; 2) деформации и напряжения, образующиеся вследствие различия коэффициентов линейного расширения соединяемых материалов; 3) деформации и напряжения, возникающие в результате образования фазовых прослоек с различными удельными объемами и коэффициентами линейного расширения; 4) деформации и напряжения, возникающие в паяных соединениях в результате структурных превращений в паяемом материале и шве.

Следует строго различать поведение конструкции (определяемое ее макроскопическими характеристиками) и поведение граничных (переходных) слоев, отличающихся своими локальными характеристиками. Поскольку в паяных соединениях связаны материалы с различными деформационными характеристиками, в большинстве случаев при внешней механической нагрузке в переходном объеме «основной материал – шов» возникает сложнонапряженное состояние, которое необходимо учитывать при оценке прочности. При действии постоянных нагрузок практически во всех видах соединений распределение напряжений в шве неодинаково как по толщине, так и по длине.

Прочность соединений определяется прежде всего особенностями напряженного состояния в паяном шве. Анализ напряженного состояния паяного соединения как многоэлементной системы, состоящей из разнородных по деформационным и прочностным свойствам материалов, весьма затруднителен. Если считать, что напряжения в шве не превышают предела упругости припоя, то для паяных соединений можно использовать данные, полученные для клеевых и адгезионных соединений.

Как правило, получить равнопрочные стыковые паяные соединения не удается. Поэтому для оценки прочности этих соединений важно знать особенности напряженного состояния в шве. Как отмечалось выше, металл различных участков соединений является неоднородным. Механические свойства металла характерных участков соединения оказываются различными вследствие того, что были применены те или иные материалы, различные методы и режимы пайки. В результате даже несложное соединение представляет собой сочетание нескольких зон различных размеров, металл которых отличается по своим механическим свойствам. Кроме того, поведение под нагрузкой металла каждой зоны определяется не только ее свойствами, но и влиянием соседних зон.

Особые трудности представляет для анализа граничный, или переходный слой. В этом слое имеет место взаимодиффузия материалов и ряд других явлений, благодаря которым получается как бы новый материал со свойствами, не аддитивными по отношению к свойствам контактирующих слоев. Границы такого «стыка» геометрически также трудно определимы, как и его свойства. Поэтому приходится при анализе прибегать к некоторым упрощающим допущениям, вплоть до признания границы раздела двух элементов. Однако необходимо отчетливо представлять себе, что таковой границы может и не существовать. В стыковых соединениях между соединяемыми материалами и припоем образуются диффузионные прослойки, что приводит к повышению прочности и снижению пластичности паяного шва. Хотя природа возникновения прослоек может быть различной, механизм их влияния на свойства соединений определяется усложненным напряженным состоянием, которое возникает при совместной деформации отличных по свойствам материалов. Поэтому количественный анализ влияния механической неоднородности должен выполняться на основе анализа напряженного состояния и, в первую очередь, напряженного состояния мягких прослоек, которые являются локализаторами разрушения и часто лимитируют несущую способность всего соединения.

Полагая, что соединение состоит только из двух идеально упругопластических материалов М и Т (рис. 1.1) с одинаковыми упругими характеристиками, но значительно отличающимися пределами текучести 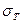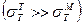, можно представить следующую схему работы поперечной мягкой прослойки при одноосном растяжении (сжатии).

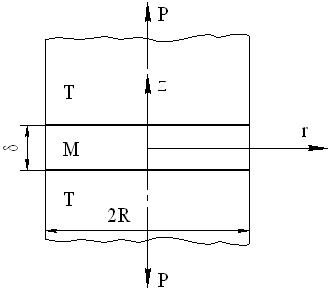
Рис. 1.1. Схема растяжения цилиндрического образца с мягкой прослойкой

В стадии упругой работы прослойка М и более прочные части Т находятся в однородном линейном напряженном состоянии. Когда средние напряжения в ходе нагружения достигают величины предела текучести мягкой прослойки 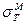, эта прослойка сразу и во всем объеме переходит в пластическое состояние.

Уровень напряжений, необходимый для начальной деформации некапиллярных швов, одинаков для различных способов пайки (газопламенная, индукционная, печная), поскольку он определяется соотношением между пределами текучести основного металла и припоя [3].

Развитие пластических деформаций сдерживается прочными частями Т, которые продолжают работать упруго. На контактных поверхностях возникают и при дальнейшем нагружении растут касательные напряжения. Прослойка М теперь уже находится в объемном напряженном состоянии, которое с ростом нагрузки все более отдаляется от одноосного растяжения. Нагрузка будет расти до тех пор, пока касательные напряжения τ не достигнут по всей площади контактных поверхностей величины 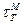– предела текучести материала прослойки при чистом сдвиге.

Cчитают [3], что в результате однократного нагружения выше 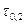некоторое разупрочнениешва связано с освобождением заторможенных на различных дефектах дислокаций и их частичной аннигиляцией, приводящей к уменьшению их средней плотности (для стальных образцов, паяных латунью). При дальнейшем нагружении начинается множественное скольжение, сопровождающееся образованием эффективных барьеров при пересечении подвижных дислокаций (в виде сидячих дислокаций).

При растяжении цилиндрических образцов с мягкой поперечной прослойкой (см. рис. 1.1) переход прослойки в пластическое состояние сдерживается более твердой основой, в результате чего в центре прослойки получает развитие трехосное растяжение.

Жесткость напряженного состояния в прослойке существенно зависит от ее геометрических размеров. Кроме геометрических параметров прослойки, на напряженное состояние влияет соотношение механических свойств материалов основы образца и прослойки. В стыковых соединениях, выполненных припоями, 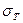которых существенно меньше 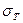соединяемых деталей, возможно возникновение гидростатического напряженного состояния в шве. В этом случае нормальное напряжение при разрушении может в несколько раз превышать 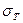припоя. Поскольку возникает фактическое упрочнение шва, то для стыковых соединений можно рекомендовать использование высокопластичных припоев.

Простейшее статически возможное поле напряжений в мягкой прослойке можно задать следующим образом (см. рис. 1.1):

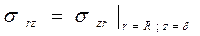
При поперечных нагрузках стыковых соединений возможен срез соединения под действием касательных напряжений, значение которых может быть определено по тем же формулам, что и для нахлесточных соединений. В этом случае для анализа напряженно- деформированного состояния рекомендуют использовать аппарат расчета соединений многослойной структуры.

Определение прочности стыковых соединений при продольных нагрузках требует учета ряда особенностей напряженного состояния в шве, связанных с его упругостью, пластичностью и ползучестью.

Даже при небольших упругих деформациях напряженное состояние в шве стыковых паяных соединениях при продольных нагрузках неоднородно. В соединениях, паяных низкотемпературными припоями, податливость которых существенно выше податливости соединяемых деталей, наблюдается концентрация осевых и касательных напряжений. Однако оценки показывают, что касательные напряжения составляют 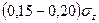,где 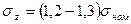- осевые напряжения (см. рис. 1.1), 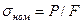– номинальное напряжение в стыковом соединении, 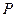– осевая нагрузка, 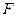– площадь поперечного сечения соединения. Поэтому при оценке прочности соединений, работающих в пределах упругих деформаций, особенности деформирования шва можно не учитывать, принимая соединение однородным по длине.

При пластических деформациях распределение напряжений в шве отличается от распределения напряжений, имеющих место при упругих деформациях. При пластических деформациях, возникающих в швах соединений, полученных с применением низкотемпературных припоев, происходит перераспределение напряжений. При совпадении или незначительном отличии модулей упругости припоя и основного материала напряжения в шве цилиндрических деталей (см. рис. 1.1) в окрестности контактной границы определяют по формулам:

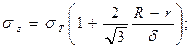
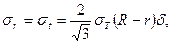
где σ _Т – предел текучести припоя при одноосном растяжении.

Таким образом, максимальные напряжения возникают по оси ПС (r = 0);

при уменьшении толщины паяного шва напряжения резко возрастают. Фактически это говорит о том, что при достижении на периферии шва предела текучести σ _Т практически весь шов перестает сопротивляться нагрузке. Прочность таких соединений определяется из условия, что номинальные напряжения в шве не превосходят .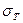

В условиях пластического течения шва несущая способность соединения существенно зависит от относительной толщины шва

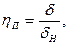
где 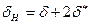(рис. 1.2).

Несущая способность ПС повышается при уменьшении .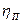

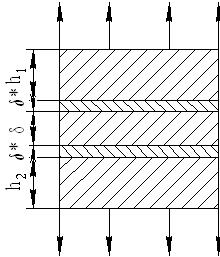
Рис. 1.2. Стыковое соединение призматических деталей: 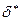- толщина диффузионной зоны; 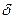- толщина шва

Расчеты показывают, что размеры стыковых соединений существенно

влияют на максимальные касательные напряжения 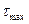. Увеличение толщины деталей 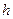в 2 раза приводит к уменьшению 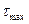в 1,5 раза; увеличение толщины шва 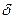в 2 раза вызывает уменьшение 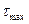в 1,3 раза. Изменение жесткости материала соединяемых деталей также заметно влияет на 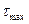. Так, в соединениях алюминиевых деталей 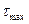в 1,4 раза меньше, чем в паяных соединениях медных деталей (припой ПСр 3).

Несущая способность соединения определяется, в том числе относительной толщиной твердой прослойки и механической неоднородностью соединения (коэффициентом механической неоднородности) 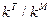(k^T, k^M – параметры пластичности, характеризующие стадию пластического течения для прослойки и основного металла соответственно). Использование решения задачи о растяжении пластичной прослойки для расчета несущей способности соединений при пластическом течении шва показало, что несущая способность соединений существенно зависит от зазора, причем она повышается при его уменьшении. Повышение несущей способности стыковых соединений наблюдается и при неоднородном шве, центральная часть в котором более пластична. Сопротивление разрушению стыковых паяных соединений 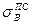, как правило, больше, чем нахлесточных ( 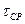). Отношение 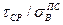зависит от формы испытываемых образцов и процессов, протекающих при пайке, свойств паяемого металла и припоя, и не является постоянной величиной.

Высокая концентрация напряжений в зоне спая может приводить к отрыву припоя от основного металла. Поэтому при пайке жестких деталей достаточно податливым припоем особое внимание следует уделять совместимости припоя с основным материалом для создания качественного спая. С этой целью может быть выполнена механическая обработка поверхностей соединяемых деталей [2].

Вследствие сложности анализа не учитывается дефектность ПС и фактически неоднородное распределение участков контакта, и местная концентрация напряжений.

Будем считать, что напряжения в шве нахлесточного соединения не превышают предела упругости припоя. При плоском напряженном состоянии в шве в результате относительного сдвига деталей и искривления соединения от изгибающего момента, возникающего из-за несовпадения линий действия сил Р (рис. 1.3), в соединении формируются касательные напряжения 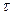и нормальные напряжения 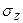и 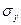, неравномерно распределенные как по длине, так и по толщине паяного шва.

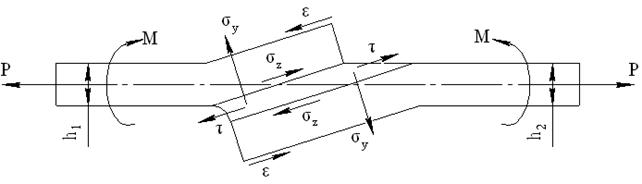
Рис. 1.3. Деформации и напряжения в элементе нахлесточного соединения:

σ _z – осевое напряжение; σ _у – отрывное напряжение

В паяном шве в окрестности зоны спая наблюдается концентрация касательных напряжений 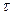, которая тем выше, чем больше отношение модулей упругости основного материала соединяемых деталей Е₁, Е₂ к модулю упругости припоя Е. В зоне спая припой практически жестко связан с основным материалом, поэтому сдвиговые деформации 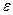в паяном шве вблизи этой зоны наиболее интенсивны и в объем паяного шва передаются через податливые слои припоя, что приводит к снижению напряжений.

Неоднородно напряженное состояние по длине паяного соединения. Нормальные напряжения 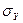от изгибающего момента в основном сосредоточены на краях соединения в области галтели (рис. 1.4). Там же развиваются максимальные сдвиговые деформации паяного шва, возникающие из-за неоднородности растяжения соединяемых деталей, на краях соединения возникает концентрация напряжений и максимальные касательные 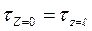превосходят средние напряжения 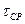(рис. 1.5). Следует отметить, что в средней части нахлесточного соединения напряжения в паяном шве чисто касательные [4]. Напряжения 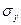в объеме галтели растягивающие, а в нахлесточном менее нагруженном участке образца меняют свой знак. Подобное распределение напряжений 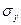подчеркивает особую роль, которую играет галтель в обеспечении прочности паяного нахлесточного соединения [4].

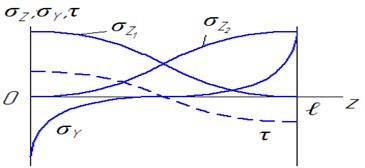
Рис. 1.4. Характер распределения напряжений по длине нахлестки

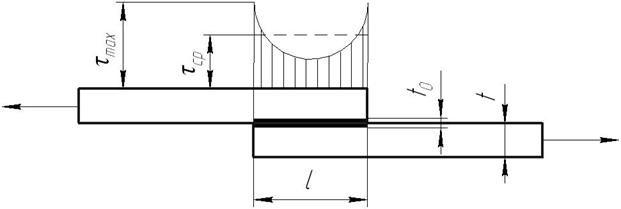
Рис. 1.5.Схема распределения касательных напряжений в нахлесточном соединении

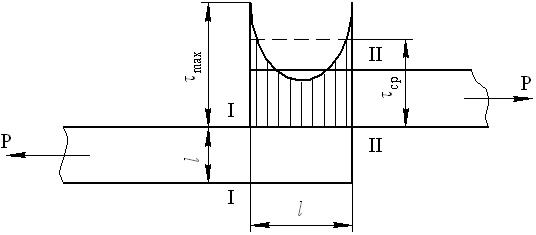
Рис. 1.6. Распределение касательных напряжений по длине шва в упругой области деформирования основного материала образца

В случае соединения элементов с равными площадями поперечных сечений в упругой области деформирования основного материала (в сечениях I – I и II – II) (рис. 1.6) максимальное значение касательного напряжения на единицу длины ПС в концевых точках определяется уравнением

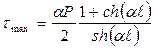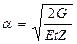; , (1.1)

где 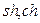- гиперболические функции; 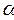- коэффициент, учитывающий механические свойства, толщину образца и величину зазора; 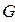- модуль упругости материала прослойки при сдвиге; 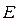- модуль нормальной упругости основного материала; 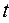- толщина образца; 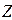- величина зазора; ℓ - длина нахлестки.

Эпюра сдвигающих напряжений представляет собой гиперболическую синусоиду (рис. 1.7).

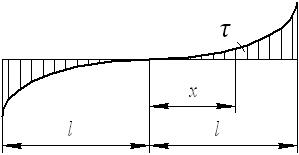
Рис. 1.7.

Из зависимости (1.1) длина нахлестки при допущении близости средних напряжений среза 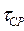к максимальным :

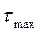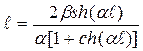(1.2)

Зависимость (1.2) для практических расчетов неудобна, так как 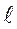не выражена явно, а находится под знаком гиперболических функций. С целью упрощения разложим функцию, входящую в выражение (1.2), в степенной ряд и решим уравнение относительно первых трех членов.