Самостоятельная работа
1. Порожнему прицепу тягач сообщает ускорение а1 = 0,4 м/с2, а груженому а2 = 0,1 м/с2. Какое ускорение сообщит тягач обоим прицепам, соединенным вместе? Силу тяги тягача считать во всех случаях одинаковой.
2. В известных опытах Отто фон Герике (1654 г.) с магдебургскими полушариями по изучению атмосферного давления, чтобы разнять два полушария, из которых был выкачан воздух, впрягали 16 лошадей (по 8 к каждому полушарию). Можно ли обойтись меньшим количеством лошадей?
3. Какие силы надо приложить к концам проволоки, жесткость которой 100 кН/м, чтобы растянуть ее на 1 мм? (F = 100 Н)
4. На сколько удлинится рыболовная леска жесткостью 0,5 кН/м при поднятии вертикально вверх рыбы массой 200 г? (4 мм)
5. Две пружины разной длины, скрепленные одними концами растягивают за свободные концы руками. Пружина жесткостью 100 Н/м удлинилась на 5 см. Какова жесткость второй пружины, если ее удлинение равно 1 см? (500 Н/м)
6. Найти удлинение буксирного троса жесткостью 100 кН при буксировке автомобиля массой 2 т с ускорением 0,5 м/с2. Трением пренебречь.
7. В 1970 г. советский космический аппарат «Луноход 1» массой 750 кг достиг поверхности Луны. Найти силу тяжести, действующую на аппарат на поверхности Земли и на поверхности Луны. gз = 9,8 м/с2, gл = 1,6 м/с2.
8. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
9. Найти силу гравитационного взаимодействия Земли и Луны.
10. Во сколько раз уменьшится сила притяжения к Земле космического корабля при его удалении от поверхности Земли на расстояние, равное радиусу Земли? Пяти радиусам Земли?
11. Каково ускорение свободного падения на высоте, равной половине радиуса Земли?
12. Средний радиус планеты Меркурий 2420 км, а ускорение свободного падения 3,72 м/с2. Найти массу Меркурия.
Контрольная работа
1. Сформулируйте закон инерции Галилея (первый закон Ньютона).
2. Какое тело называется свободным? Есть ли на самом деле в природе свободные тела?
3. В каком случае тело можно считать свободным?
4. Назовите силы, которые могут оказывать воздействие на тело (4 типа).
5. О существовании каких систем отсчета утверждается в первом законе Ньютона?
6. Какая система отсчета называется инерциальной?
7. Какая система отсчета называется неинерциальной?
8. Что называют инертностью тела?
9. Что такое масса?
10. Дайте определение понятию сила.
11. В каком случае сила полностью определена?
12. В каком случае возникает сила упругости?
13. Какие виды деформаций тел вы знаете? Приведите примеры.
14. Какая деформация называется упругой?
15. Какая деформация называется пластической?
16. Для каких деформаций справедлив закон Гука?
17. Сформулируйте закон Гука и поясните все величины в него входящие.
18. Когда возникает сила трения?
19. Запишите формулу для силы трения и поясните величины в нее входящие.
20. Запишите какие виды сил трения существуют в природе. В каком случае возникает тот или иной вид сил трения?
21. В каком случае возникает сила вязкого трения?
22. От чего зависит сила вязкого трения?
23. Какую силу называют силой тяжести?
24. К чему приложена сила тяжести?
25. Запишите по какой формуле определяется сила тяжести и поясните все величины в нее входящие.
26. Что такое ускорение свободного падения? С одинаковым ли ускорением будут падать кирпич и перышко?
27. Что такое вес тела? К чему он приложен?
28. Сформулируйте второй закон Ньютона и поясните все величины в него входящие.
29. Сформулируйте третий закон Ньютона. Как вы думаете, справедлив ли третий закон Ньютона в мире элементарных частиц? Поясните свою позицию.
30. Сформулируйте закон всемирного тяготения.
31. Запишите численное значение гравитационной постоянной и ее единицу измерения.
32. Какой физический смысл имеет гравитационная постоянная?
Закон сохранения импульса.
Законы сохранения в механике имеют важное значение в механике в частности и в физике вообще. Они позволяют сравнительно просто без рассмотрения действующих на тело сил и без прослеживания движения тел системы решать ряд практически важных задач.
| Законы сохранения (были открыты в механике, но играют огромную роль во всей физике) | ||
| Закон сохранения импульса | Закон сохранения энергии | Закон сохранения момента импульса |
| Связан с однородностью пространства: перенос (сдвиг) в пространстве любой механической системы никак не влияет на процессы, происходящие внутри нее. | Связан с однородностью времени: все моменты времени равноправны и можно принять любой из них за начало отсчета времени. | Связан с изотропностью пространства: свойства пространства одинаковы по всем направлениям. |
Законы сохранения применяются даже тогда, когда законы механики Ньютона применять нельзя (например, при движении электронов в атомах). Законы сохранения применимы к телам обычных размеров, к космическим телам и элементарным частицам.
Таким образом, важность законов сохранения состоит в том, что они являются всеобщими, то есть применяются ко всем явлениям природы.
Особенно они незаменимы, когда исследователи начинают проникать во вновь открытую сферу науки, которая еще толком неизвестна, как было, например, при открытии элементарных частиц.
Связь законов сохранения со свойствами пространства и времени была установлена только в 20 веке.
С помощью основных законов механики – второго и третьего законов Ньютона – можно решить любую механическую задачу. Применение законов Ньютона к решению задач можно облегчить, используя следующий вывод из второго закона:
Подействуем на тело массы m постоянной силой F. Тогда ускорение тела будет постоянно и равно: a=F/m
Пусть в начальный момент промежутка времени t, в течение которого действовала сила, скорость тела была v0, а в конечный момент этого промежутка скорость тела стала равна v.
В случае постоянного ускорения a=(v-v0)/Δt. Подставив в формулу для a, получим: mv - mv0 = FΔt
среднее значение силы за рассматриваемый промежуток времени.
Произведение mv – называется импульсом материальной точки и обозначается буквой p: p = mv.
Импульсом материальной точки называют величину, равную произведению массы точки на ее скорость.
Импульс – векторная величина, всегда совпадающая по направлению с вектором скорости: v↑↑p.
Обозначим p1=mv1 – импульс материальной точки в начальный момент интервала Δt, p2=mv2 - импульс материальной точки в конечный момент интервала Δt. Тогда p2 - p1 = Δp - изменение импульса материальной точки за время Δt: Δp = FΔt . Вектор силы совпадает по направлению с вектором изменения импульса, так как Δt > 0.
Таким образом, изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление, как и сила.
В такой форме второй закон Ньютона выглядит следующим образом: F =  . Именно так второй закон Ньютона был первоначально сформулирован.
. Именно так второй закон Ньютона был первоначально сформулирован.
Произведение FΔt – иногда называют импульсом силы.
Уравнение Δp = FΔt – показывает, что одинаковые изменения импульса материальной точки могут быть получены в результате:
1. Действия большой силы в течение малого промежутка времени.
2. Действие малой силы в течение большого интервала времени.
Эту формулу можно обобщить на случай , когда сила F изменяется во времени. Для этого весь промежуток Δt действия силы можно разделить на малые интервалы Δti, чтобы на каждом из них значения силы можно было считать постоянным. Для каждого такого интервала справедлива формула: Δp = FΔt. Суммируя Δp по всем Δti, получим: Δp = 
Импульс системы материальных точек:
Импульс системы материальных точек равен векторной сумме импульсов всех точек системы.
Изменение импульса системы тел:
Совокупность тел, движение которых изучается называется механической системой.
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению:
Δpс = 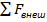 Δt
Δt
Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Дата добавления: 2017-05-02; просмотров: 1390;











