Прямая и обратная геодезические задачи
При вычислительной обработке выполненных на местности измерений, при проектировании инженерных сооружений и расчетах для перенесения проектов в натуру возникает необходимость решения прямой и обратной геодезических задач.
Прямая геодезическая задача. По известным координатам х1 и у1 точки 1, дирекционному углу a1-2 и расстоянию d1-2 до точки 2 требуется вычислить ее координаты х2, у2.
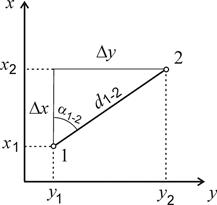 Рис. 5.4. К решению прямой и обратной геодезических задач
Рис. 5.4. К решению прямой и обратной геодезических задач
| Координаты точки 2 определяются по формулам (рис. 5.4):
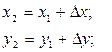 (3.4)
где приращения координат Dх, Dу равны (3.4)
где приращения координат Dх, Dу равны
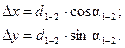 (3.5) (3.5)
|
Обратная геодезическая задача. По известным координатам х1, у1 точки 1 и х2, у2 точки 2 требуется вычислить расстояние между ними d1-2 и дирекционный угол a1-2.
Из формул (3.5) и рис. 5.4 видно, что 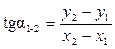 . (3.6)
. (3.6)
Для определения дирекционного угла a1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса w = 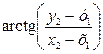 , лежащее в диапазоне -90°£w£ +90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a < 360°.
, лежащее в диапазоне -90°£w£ +90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a < 360°.
Формула перехода от w к a зависит от координатной четверти, в которой расположено заданное направление или, другими словами, от знаков разностей Dy = y2 - y1 и Dx = х2 - х1(см. таблицу).
| I четверть | П четверть | Ш четверть | IV четверть | |
| Dх | + | - | - | + |
| Dу | + | + | - | - |
| w | + | - | + | - |
| Формулы | a=w | a=w+180° | a=w+180° | a=w+360° |
Расстояние между точками вычисляют по формуле
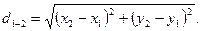 (3.6)
(3.6)
или другим путем – по формулам
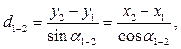
 (3.7)
(3.7)
Программами решения прямых и обратных геодезических задач снабжены, в частности, электронные тахеометры, что дает возможность непосредственно в ходе полевых измерений определять координаты наблюдаемых точек, вычислять углы и расстояния для разбивочных работ.
Дата добавления: 2017-05-02; просмотров: 2507;











