МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА

Пусть решается задача определения условного экстремума функции 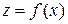при ограничениях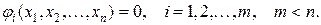

Составим функцию

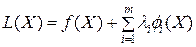, (22)

которая называется функцией Лагранжа. λ_i - постоянные множители (множители Лагранжа). Отметим, что множителям Лагранжа можно придать экономический смысл. Если 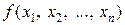- доход, соответствующий плану 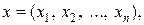а функция 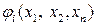- издержки i-го ресурса, соответствующие этому плану, то λ_i - цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка). 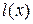- функция 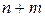переменных 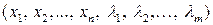. Определение стационарных точек этой функции приводит к решению системы уравнений

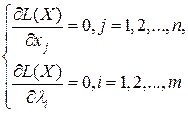(23)

Легко заметить, что 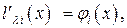т.е. в (23) входят уравнения связи. Таким образом, задача нахождения условного экстремума функции 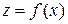сводится к нахождению локального экстремума функции l(x). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума - исследования знака второго дифференциала 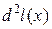в стационарной точке при условии, что переменные приращения 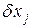, связаны соотношениями

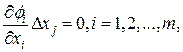(24)

полученными путем дифференцирования уравнений связи.