Классификация потерь напора

Одним из важнейших вопросов гидромеханики является определение потерь энергии при движении жидкости. При движении жидкости по трубопроводам возникают потери энергии, которые зависят от длины трубопроводов (пропорциональные длине канала) и потери энергии в местных сопротивлениях – запорная арматура, повороты, расширения и сужения трубопроводов – вызываемые изменениями скорости потока либо по величине, либо по направлению. Потери энергии потока как на преодоление сопротивлений по длине трубопроводов, так и на преодоление местных сопротивлений, в конечном счете обусловлены вязкостью жидкости, а, следовательно, теряемая механическая энергия рассеивается и переходит в тепловую.

Важность определения потерь напора 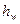(или потерь давления 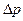) связана с необходимостью расчета затрат энергии, требуемых для компенсации этих потерь при перемешивании жидкостей, например, с помощью насосов, компрессоров и т.д.

Потерянный напор является суммой двух слагаемых:

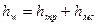(98)

где 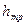, 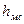- потери напора вследствие трения и местных сопротивлений, соответственно.

Для вычисления потерь напора при турбулентном режиме обычно пользуются частными эмпирическими формулами

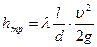(99)

и

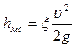(100)

где		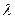- коэффициент гидравлического трения;
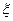
		- коэффициент местного сопротивления;
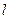
		- длина трубопровода, ;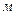
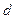
		- диаметр трубы, ;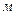
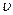
		- средняя скорость движения жидкости в трубопроводе, ;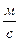
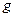
		- ускорение свободного падения, .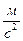

Средняя скорость, входящая в формулы (99) и (100) – эта такая, одинаковая для всех точек сечения скорость, при которой за единицу времени через данное сечение проходит тот же расход жидкости, что и при действительном распределении скоростей по сечению потока. Среднюю скорость определяют по уравнению расхода

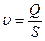(101)

где		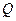- объемный расход, т.е. объем жидкости, проходящий через живое сечение потока за единицу времени, жидкости, ;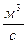
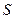
		- живое сечение потока (в случае течения по трубе, равное площади поперечного сечения трубы, .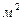

Из формул (99) и (100) следует, что потери энергии на трение и местные сопротивления пропорциональны скоростному и динамическому напору ( 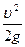), который является мерой кинетической энергии потока, отнесенной к единице объема жидкости. В действительности эта зависимость значительно сложнее, так как коэффициент трения и коэффициент местного сопротивления не являются постоянными величинами, а существенно зависят от скорости течения жидкости, ее плотности и вязкости, а также диаметра и шероховатости трубы, по которой движется поток.

Величина коэффициента трения проявляется по-разному при различных режимах движения потока в трубе. В одном диапазоне чисел Рейнольдса, характеризующих режим движения, на величину 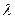влияет в большей степени скорость, в другом диапазоне преобладающее влияние оказывают геометрические характеристики – диаметр и шероховатость трубы (высота выступов шероховатости ).

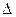В связи с этим различают четыре области сопротивления, в которых изменение 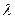имеет свою закономерность.

Первая область – область ламинарного потока, ограниченная значениями 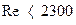, в которой 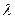зависит от 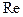и не зависит от величины 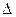, определяется по формуле Пуазейля

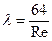. (102)

При этом значении 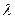потери напора по длине трубы пропорциональны скорости в первой степени. Все остальные области сопротивления находятся в зоне турбулентного режима с различной степенью турбулентности.

Вторая область – гидравлически гладкие трубы. Поток в трубе при этом турбулентный, но у стенок трубы сохраняется слой жидкости, в пределах которого движение остается ламинарным. Трубы считаются гидравлически гладкими, если толщина ламинарного слоя 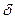больше высоты выступов шероховатости 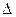. В этом случае ламинарный слой покрывает неровности стенок трубы и последние не оказывают тормозящего влияния на основное турбулентное ядро потока.

Границу зоны гидравлически гладких труб можно определить из зависимости:

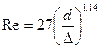(103)

Для гидравлически гладких труб, т.е при условии 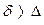коэффициент 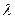может быть определен по формуле:

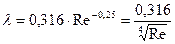, (104)

которая применима при значениях чисел Рейнольдса .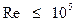

Третья область – переходная от области гидравлически гладких труб к квадратичной области. В этой области толщина ламинарного слоя 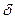равна или меньше выступов шероховатости 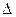, которые в этом случае выступают как препятствие у стенок, увеличивая турбулентность, а, следовательно, и сопротивление в потоке.

Для определения 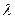в переходной области сопротивления применима формула

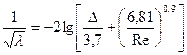(105)

Потери напора по длине трубы в переходной области сопротивления пропорциональны скорости в степени от 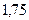до .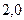

Четвертая область – гидравлически шероховатых труб или квадратичного сопротивления (автомодельная область). Основное влияние на сопротивление потоку оказывает шероховатость стенок трубы. Чем больше выступы шероховатости 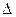, тем большую турбулентность они вызывают, тем больше будут затраты энергии в потоке на преодоление сопротивлений. В квадратичной области сопротивления коэффициент 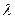не зависит от скорости, а становится функцией только относительной шероховатости 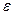, выражаемой отношением абсолютной шероховатости 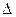к диаметру трубы

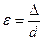(106)

Для автомодельной области в уравнении (105) можно пренебречь вторым слагаемым в квадратных скобках, и оно принимает вид

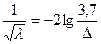. (107)