Турбулентное движение.

Турбулентное состояние потока характеризуется непрерывным перемешиванием множества мельчайших водоворотных образований, возникающих у твердых границ и перемещающихся внутрь потока.

Зарождение водоворотных образований обязано вязкости жидкости. На поверхности контакта жидкости и твердых стенок молекулы жидкости и молекулы твердых стенок находятся на расстоянии силового их взаимодействия. В связи с этим частицы жидкости непосредственно у стенок задерживаются, и скорость их равна нулю. Соседние с ними частицы приходят в движение, и их скорость возрастает с удалением от стенок. При этом возникает вращательное движение отдельных масс жидкости.

Сложение двух движений - поступательного и вращательного - возбуждает силу, приложенную к массе частицы и направленную нормально к продольной скорости потока (эффект Магнуса). Под действием этой силы частицы жидкости перемещаются в центральную область потока, образуя процесс перемешивания. Наличие шероховатости стенок содействует такому перемешиванию и в некоторых случаях может оказаться даже главной причиной явления. Этот процесс, очевидно, возможен при достаточно больших скоростях течения, при которых стабилизирующее воздействие вязкости не может воспрепятствовать такому перемешиванию. Известно, что турбулентное движение возникает при скоростях больше 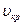(когда число Рейнольдса больше ).

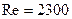Процесс перемешивания обуславливает возникновение пульсации скоростей, т.е. такое изменение ее величины в данной точке, при котором отклонения от некоторой средней происходят в обе стороны. Объясняется это тем, что через данную точку пространства последовательно проходят разные частицы жидкости с разными скоростями как по величине, так и по направлению.

Обычно наибольшее внимание уделяется явлению пульсации продольной скорости 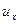, измеряемой в точке поперечного сечения с помощью различных гидрометрических приборов.

В связи с явлением пульсации турбулентное движение оказывается неустановившимся, и в любой момент времени имеет место мгновенное поле скоростей (и других кинематических параметров потока). При этом возможно говорить о средних значениях скорости за тот или иной промежуток времени. Чем больше промежуток времени осреднения, тем точнее определяется данная величина. Определенная таким образом скорость называется осредненной скоростью в данной точке.

Связь между мгновенной и осредненной скоростью определяется так:

,

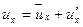где 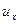, , 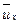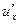- соответственно мгновенная, осредненная и пульсационная составляющие скорости.

Процесс перемешивания вызывает перенос количества движения из области малых скоростей потока в область больших скоростей и обратно. Очевидно, массы с малыми скоростями при входе в область течений с большими скоростями будут тормозить движение в этой области, т.е оказывать силовое противодействие движению. Это будут силы инерции, и, следовательно, физическая природа турбулентных сопротивлений – инерционная. Масса жидкости с большими скоростями, оказывая давление на присоединенные массы, ускоряют их движение и расходуют при этом свою энергию (при этом ускорении возникают силы инерции).

Прандтль при установлении закона распределения скоростей принял следующую схему течений в трубопроводе.

У стенок трубы скорости принимаются нулевыми, к центру (оси трубы) они постепенно увеличиваются, т.е. у стенок трубы создается ламинарный слой небольшой толщины, за пределами которого располагается центральная основная часть потока – турбулентное ядро. В связи с малыми скоростями течения в ламинарном (пристенном) слое скорости быстро нарастают, градиент скорости здесь велик, и его можно приближенно считать величиной постоянной. В пределах центрального ядра турбулентное течение и изменение скоростей происходят не так интенсивно. Иллюстрация такой схемы показана на рис. 33.

Для ламинарного режима касательные напряжения определяются по формуле Ньютона

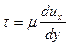
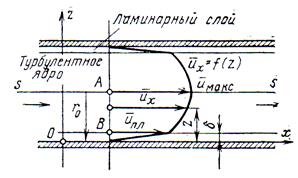
Рис. 33. Эпюра скоростей при турбулентном режиме движения

При турбулентном режиме движении

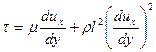. (92)

где 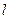- путь перемешивания, аналогичен средней длине пробега молекул в кинетической теории газов.

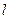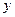По данным исследований Г.А. Гуржиенко, вблизи стенок трубы зависимость от оказалась линейной, поэтому можно написать

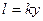(93)

где 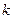- коэффициент пропорциональности, называемый универсальной постоянной.

По Г.А. Гуржиенко, 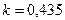. Следовательно, 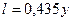. Первый член 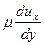характеризует вязкостное трение, которое соответствует силам трения в ламинарном движении. Второй член 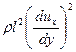выражает дополнительное касательное напряжение от пульсации, возникающей в турбулентном потоке из-за наличия поперечного движения отдельных частиц жидкости. С увеличением скорости течения (числа Рейнольдса) главное влияние на величину касательных напряжений оказывает второй член в уравнении (92) и при больших числах Рейнольдса касательные напряжения оказываются пропорциональными квадрату градиента скорости.

Благодаря пульсации в турбулентном потоке жидкости закон распределения скоростей по живому сечению иной, чем при ламинарном. При турбулентном движении происходит выравнивание скоростей по сечению.

Для развитого турбулентного режима движения жидкости ввиду малой ее массы, участвующей в пограничном слое, первый член правой части уравнения (92) по сравнению со вторым членом является малой величиной. поэтому им можно пренебречь. Тогда уравнение (92) будет иметь вид

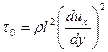(94)

Или

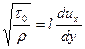(95)

Подставляя значение 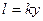в формулу (95) и обозначая 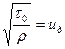, будем иметь

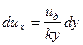, (96)

где 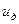- называется динамической скоростью, так как имеет размерность скорости.

Примем 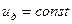, тогда после интегрирования дифференциального уравнения (96) получим логарифмический закон распределения скоростей по сечению для турбулентного потока:

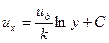. (97)