Мультиплексоры и демультиплексоры
Мультиплексор (MUX – multiplex- многократный) позволяет коммутировать в численном порядке информацию, поступающую с нескольких входных шин на одну выходную. С его помощью осуществляется временное разделение информации, поступающей по разным каналам.
Схема мультиплексора на 2 входа приведена на рис. 2.9.
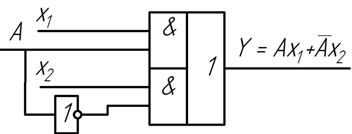
Рис. 2.9 Схема двухвходового мультиплексора
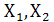 – информационные входы
– информационные входы
А – адресный вход
В зависимости от значения 1 или 0, подаваемых на адресный вход, на выходе Y формируется сигнал 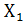 или
или 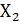 . Это логическая структура мультиплексора вида 2:1. Читается: две линии к одной.
. Это логическая структура мультиплексора вида 2:1. Читается: две линии к одной.
Логическая структура мультиплексора вида 4:1, составляющая ½ микросхемы К155КП2 приведена на рис. 2.10.
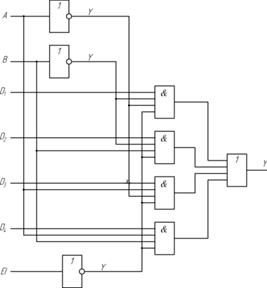
Рис. 2.10 Структурная схема мультиплексора вида 4:1
D1 – D4 – информационные входы
А, В – адресные входы
А – младший разряд
В – старший разряд
ЕI – разрешающий вход
Если EI=1, то на схемы И поступает 0 и мультиплексор не работает, то есть работа возможна только при EI=0.
В табл. 2.2 приведены все возможные сочетания входных воздействий и отклики мультиплексора.
Таблица 2.2
Мультиплексор вида 4:1
| Входы | Выход Y | ||
| Е | А | В | |
| D1 | |||
| D2 | |||
| D3 | |||
| D4 | |||
| 
|
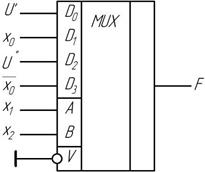
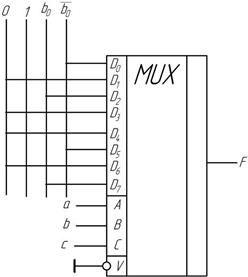
Мультиплексор К155КП1 имеет 16 информационных входов (D0 – D15) и четыре управляющих входа A, B, C, D, разрешающий вход V и один инверсный выход F. В зависимости от цифровой комбинации на управляющих входах сигналы с соответствующего информационного входа проходят в инвертированном виде на выход микросхемы. Передача информации возможна только при низком уровне на разрешающем входе.
Если требуется структура с большим количеством входов, то можно воспользоваться схемой наращивания разрядности, приведенной на рис. 2.11.
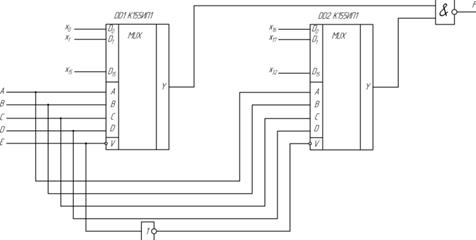
Рис. 2.1 Мультиплексор вида 32:1 на основе двух микросхем К155КП1
Адресными входами низших разрядов служат соединенные параллельно входы A, B, C и D. Разрешающие входы V в данном случае используются для подачи высшего (пятого) разряда Е: на первую микросхему в прямом виде, на вторую в инверсном. Первая микросхема работает при нулевом сигнале высшего разряда (Е=0); а вторая – при единичном (Е=1). Благодаря логическому элементу И-НЕ на выходе, выходные сигналы будут одинаковы с входными.
Мультиплексоры с Z-состоянием выходов легко позволяют увеличивать число коммутируемых каналов без привлечения дополнительных логических элементов для объединения выходов нескольких микросхем.
На рис. 2.12 приведена схема наращивания разрядности мультиплексора с использованием микросхем, имеющих Z-состояние выхода.
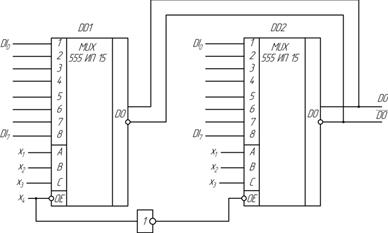
Рис. 2.12 Схема наращивания разрядности мультиплексоров, имеющих Z-состояние
Демультиплексоры
Демультиплексоры противоположны в функциональном отношении мультиплексорам, то есть их назначение распределить сигналы с одного информационного входа в желаемой последовательности по нескольким выходам.
Схема демультиплексора на 2 выхода представлена на рис. 2.13.
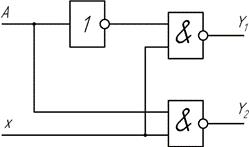
Рис. 2.13 Демультиплексор вида 1:2
 информационный вход
информационный вход
А – адресный вход
В зависимости от значения А информация 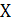 поступает на
поступает на 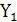 или
или 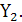
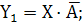
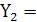
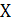 · А
· А
Логические функции демультиплексора и дешифратора сходны между собой.
Дешифратор можно рассматривать как обращенный по входам демультиплексор, у которого адресные входы стали информационными, а бывший информационный вход стал управляющим.
Рассмотрим структуру демультиплексора-дешифратора, представленного на рис. 2.14.
Работу устройства описывают следующие булевые уравнения:
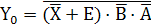
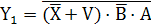
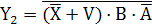
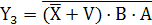
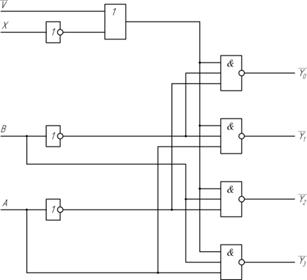
Рис. 2.14 Логическая структура демультиплексора 1:4 – дешифратора 2:4
A, B – адресные входы
Х – информационный вход
V – вход управления
В табл. 2.3 приведены режимы работы этой схемы в качестве демультиплексора и в качестве дешифратора.
Таблица 2.3
Таблица истинности демультиплексора-дешифратора
| Входы | Выходы | |||||||
| В | А | X | V | 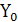
| 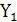
| 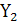
| 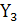
| |
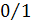
| 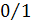
| |||||||
| DMX | 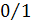
| 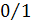
| ||||||
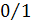
| 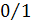
| |||||||
| 
| |||||||
| ||||||||
| DC | 
| |||||||
| ||||||||
|
Типичным представителем демультиплексора - дешифратора является интегральная микросхема К155ИД3 (аналог 74154).
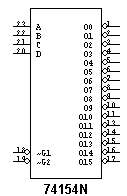
A, B, C, D – информационные входы
G1, G2 – разрешающие входы
Режим демультиплексора 1:16
G1 = 0, тогда G2 – информационный. Кодовая комбинация A-B-C-D переводит один из 16 выходов в активное состояние, которому соответствует логический 0, остальные выходы сохраняют логическую 1.
Существенно, что сигналы на активном выходе повторяют сигналы в прямом виде, поступающие на информационный вход.
Режим дешифратора 4:16
G1 = G2 = 0, тогда A-B-C-Dинформационные входы.
Если G1 или G2 равен 1, то на всех выходах, независимо от состояний входов A-B-C-D установится логическая 1.
Мультиплексоры и демультиплексоры (ДМХ) КМОП являются коммутаторами сигналов в прямом смысле, то есть могут передавать аналоговые сигналы.
MUX как универсальный логический элемент
Использование мультиплексора в качестве универсального логического элемента основано на общем свойстве логических функций независимо от числа аргументов всегда равняться логической единице или нулю. Если на адресные входы мультиплексора подавать входные переменные, зная, какой выходной уровень должен отвечать каждому сочетанию этих сигналов, то предварительно установив на информационных входах потенциалы нуля и единицы согласно программе, получим устройство, реализующее требуемую функцию.
Примеры применения мультиплексора
1. Преобразование параллельного кода в последовательный.
Одним из способов перехода от параллельного кода к последовательному может служить схема, приведенная на рис. 2.15.
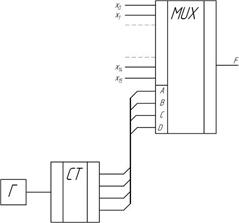
Рис. 2.15 Схема преобразования параллельного кода Х0 - Х15 в последовательный
Генератор вырабатывает импульсы, которые поступая на счетчик СТ заставляют его триггеры последовательно менять свое состояние от 0000 до 1111. Параллельный шестнадцатиразрядный код, подлежащий преобразованию в последовательный, подается на входы Х0 – Х15. Каждый из входов Х0 – Х15 соединяется с выходом MUX согласно списку состояний счетчика. Перебрав весь список, мы выведем последовательно на выход F все разряды параллельного кода.
2. Программируя информационные входы MUX согласно таблице истинности можно получить устройства, реализующие любую логическую функцию, содержащую до n+1 переменных, где n – число адресных входов мультиплексора.
Пример № 1: Реализовать на MUX функцию, заданную таблицей истинности:
| a | b | Y |
Решим этот пример двумя способами.
Решение 1. Запрограммировав каждый из информационных входов мультиплексора значениями Y, получим схему реализации этой задачи на MUX вида 4:1.
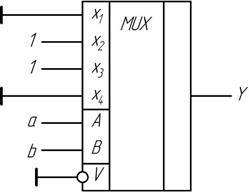
Решение 2. Воспользуемся следующим приемом: разобьем таблицу на парные строки и добавим ещё одну колонку F.
| a | b | Y | F |
| F1 = b | |||
F2 = 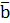
|
Видим, что в пределах одной большой строки аргумент «а» не меняется, а аргумент «b» колеблется 0-1. Оценим взаимосвязь поведения аргумента «b» и отклика функции Y. Очевидно, что в верхней строке Y повторяет значения b, а в нижней - противоположен. Следовательно, от мультиплексора требуется выполнение всего двух функций: b и b̅, а это в два раза уменьшает мощность применяемого МХ. Схема реализации той же задачи примет вид:
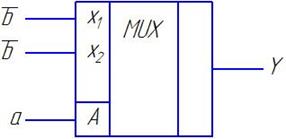
Каждый из рассмотренных способов решения имеет свои достоинства и недостатки. Так при решении задачи первым способом нам не потребуются дополнительные логические элементы – инверторы, а при втором способе потребуется один инвертор. Зато, как уже отмечалось, при втором способе решения требуется мультиплексор меньшей мощности.
Пример № 2: Функция трех переменных задана таблицей истинности:
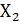
| 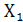
| 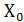
| Y | Примечание | |||
| F1 = 1 | |||||||
F2 = 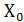
| |||||||
| F3 = 0 | |||||||
F4 = 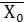
|
Расчленим мысленно таблицу истинности на группы по 2 строки в каждой (в каждой группе 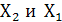 неизменны; аргумент
неизменны; аргумент 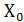 может иметь 2 состояния; F принимает одно из четырех значений:
может иметь 2 состояния; F принимает одно из четырех значений:
F1 = 1, F2 = 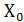 , F3 = 0, F4 =
, F3 = 0, F4 = 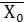
Если переменные сигналы 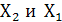 подключить к адресным входам MUX А и В, а на информационные входы
подключить к адресным входам MUX А и В, а на информационные входы 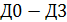 подать согласно таблице постоянные потенциалы логической единицы и нуля
подать согласно таблице постоянные потенциалы логической единицы и нуля 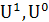 и переменные сигналы
и переменные сигналы 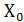 , то получим искомую схему.
, то получим искомую схему.
Пример № 3: Таблицей истинности задана функция трех переменных (мажоритарный элемент)
| a | b | с | Y | Примечание |
| F1 = 0 | ||||
| F2 = c | ||||
| F3 = c | ||||
| F4 = 1 | ||||
Решение: расчленим мысленно таблицу истинности на группы по 2 строки в каждой (в каждой группе a и b неизменны; аргумент «c» может иметь 2 состояния; F принимает одно из трех значений:
F1 = 0, F2 = с, F3 = с, F4 = 1
Реализация на MUX 4:1 с разрешающим входом 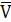
Пример № 4: Разработать схему компаратора двухразрядных чисел А и В. А = 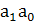 ; В=
; В= 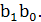
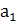
| 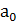
| 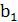
| 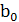
| F | Примечание |
F1 = 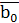
| |||||
| F2 = 0 | |||||
F3 = 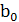
| |||||
| F4 = 0 | |||||
| F5 = 0 | |||||
F6 = 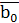
| |||||
| F7 = 0 | |||||
F8 = 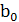
| |||||
Пример № 5: Сумматор на MUX. Составим таблицу истинности для сумм двух одноразрядных чисел А и В и функции переноса Рi . Разобьем на две строки, так, что А и В не меняют свое значение, а 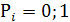 . Найдем
. Найдем 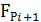 и
и 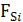 для каждой пары строк таблицы.
для каждой пары строк таблицы.
| Входы | Выходы | |||||
| А | В | 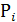
| 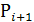
| 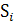
| 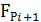
| 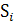
|
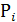
| ||||||
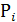
| 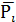
| |||||
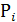
| 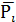
| |||||
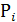
|
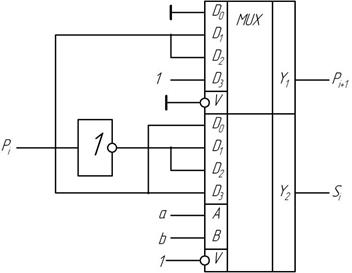
Реализация: Воспользуемся MUX К155КП2 или 564КП1 имеющими 2 четырехвходовых MUX в одном корпусе.
Лекция 6
Сумматоры
Это устройства, предназначенные для сложения чисел в двоичном и реже в 2-10 коде.
Классификация сумматоров:
1) По характеру действия: комбинационные (не имеющие памяти);
накопительные (сохраняющие результаты вычислений).
2) По способу обработки чисел: последовательного и параллельного типа.
3) По способу формирования сигнала переноса: с последовательным, сквозным и групповым переносом.
Полусумматор
S = 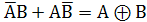 - функция суммы
- функция суммы
P = 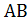 - функция переноса
- функция переноса
S – бит суммы; Р – бит переноса; 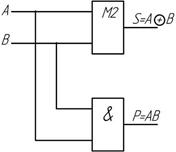
HS – half sum – полусумматор.
Обозначение на схемах
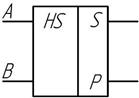
Таблица истинности полусумматора.
| Входы | Выходы | ||
| А | В | Р | S |
Развернутая схема полусумматора приведена на рис. 2.16.
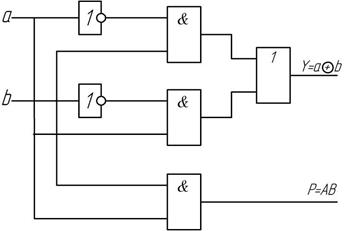
Рис. 2.16 Полусумматор
Полусумматор пригоден для сложения двух чисел только в младшем разряде. Как видно из схемы сложения двух многоразрядных чисел для n-го разряда необходим бит переноса 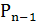 . Поэтому полный сумматор должен иметь 3 входа.
. Поэтому полный сумматор должен иметь 3 входа.
Полный сумматор
Таблица истинности сумматора
| Входы | Выходы | |||
| А | В | 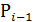
| 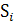
| 
|
Схема полного сумматора на элементах М2 приведена на рис. 2.17.
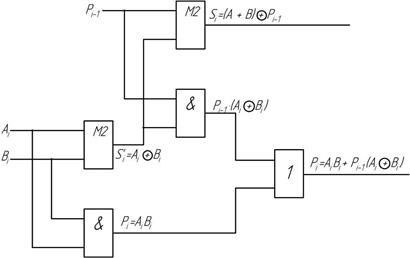
Рис. 2.17 Полный сумматор на элементах М2
Сумматор можно выполнить и на простых логических элементах (рис. 2.18).
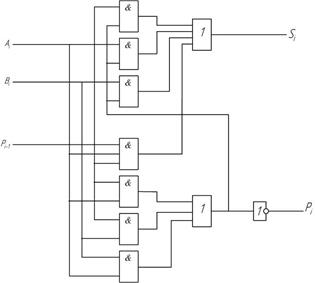
Рис. 2.18 Полный сумматор на элементарных логических элементах.
Условное обозначение одноразрядного сумматора
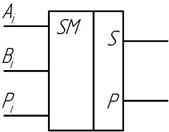
Сумматоры последовательного действия
Используется один общий для всех разрядов полный сумматор с дополнительной цепью задержки (рис. 2.19).
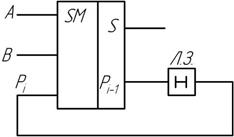
Рис. 2.19 Структура последовательного многоразрядного сумматора
Оба слагаемых кодируются последовательностями импульсов, которые синхронно вводятся в сумматор через входы А и В, начиная с младших разрядов.
Цепь временной задержки (л.з.) обеспечивает хранение импульса переноса 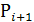 на время одного такта, то есть до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован.
на время одного такта, то есть до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован.
Достоинство: малые аппаратные затраты.
Недостатки: 1) низкое быстродействие, так как одновременно суммируется лишь пара слагаемых;
2) для хранения А и В и преобразования последовательного кода выходных импульсов S в параллельный необходимы дополнительные аппаратные затраты.
Сумматоры параллельного типа
Схема сумматора параллельного типа с последовательным переносом приведена на рис. 2.20.

Рис. 2.20 Параллельный сумматор с трактом последовательного переноса
Число сумматоров равно числу разрядов слагаемых, поэтому слагаемые А и В складываются во всех разрядах одновременно, а перенос Р поступает с окончанием операции сложения в предыдущем разряде.
Недостатки: Ограниченное быстродействие, так как формирование сигнала переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса младшего разряда не распространится последовательно по всей схеме.
Уменьшение времени распространения сигнала переноса достигается тем, что для каждого двоичного разряда дополнительно находятся два сигнала: образования переноса Gi и распространения переноса Hi.
Gi = Ai · Bi H = 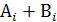
Если 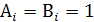 , то Gi = 1, т.е. образуется сигнал переноса Pi в высший разряд независимо от формирования функций суммы в предыдущих разрядах.
, то Gi = 1, т.е. образуется сигнал переноса Pi в высший разряд независимо от формирования функций суммы в предыдущих разрядах.
Если 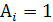 или
или 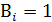 , то есть
, то есть 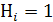 , то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего разряда.
, то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего разряда.
Если функции распространения переноса в двух соседних разрядах равны 1, то есть 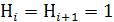 , и при этом имеется сигнал переноса
, и при этом имеется сигнал переноса 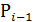 из предыдущего разряда, то перенос производится непосредственно в разряд номер i+2.
из предыдущего разряда, то перенос производится непосредственно в разряд номер i+2.
Типичными представителями сумматоров являются:
К155ИМ2 - двухразрядный
К155ИМ3 - четырехразрядный
Вычитатели (субтракторы)
SUB – обозначение вычитателей, но они как отдельные микросхемы не выпускаются, т.к. операция вычитания может быть заменена сложением и роль вычитателя может выполнить сумматор.
Операция вычитания заменяется операцией сложения уменьшаемого с вычитаемым в дополнительном коде.
Например: А – В = ?
1 пример: когда А 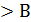
А = 111 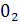 =
= 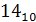
В = 100 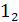 =
= 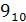
Сначала В представляют в обратном коде (1 заменить на 0, а 0 на 1), то есть 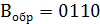 . Затем
. Затем 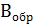 переводят в дополнительный код, то есть
переводят в дополнительный код, то есть 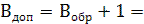
+
 1
1
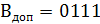 , и только потом складывают А и
, и только потом складывают А и 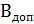 .
.
+
0111
10101
Появление подчеркнутой 1 переноса свидетельствует о том, что А 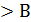 и результат - положительное число. Сама подчеркнутая единица при этом не входит в итог и отбрасывается. Оставшаяся тетрада двоичных чисел 01012 = 510 является итогом вычисления.
и результат - положительное число. Сама подчеркнутая единица при этом не входит в итог и отбрасывается. Оставшаяся тетрада двоичных чисел 01012 = 510 является итогом вычисления.
2 пример: когда 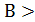 А
А
А = 100 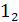 =
= 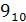
В = 111 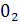 =
= 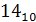
Сначала найдем 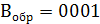 , затем
, затем 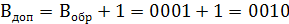
Сложим А и Вдоп
+
0011
_1011
Так как перенос 1 не наблюдается (над чертой можно поставить 0), это значит, что ответ отрицательный и получен в обратном коде. Поэтому следует проинвертировать ответ и прибавить единицу, то есть перевести в дополнительный код.
(А – В)доп = (А – В)обр + 1 = 0100 + 1 = 0101, то есть минус 510.
Интегральная схема четырехразрядного сумматора К155ИМ3 может выполнять роль как сумматора, так и вычитателя (рис. 2.21).
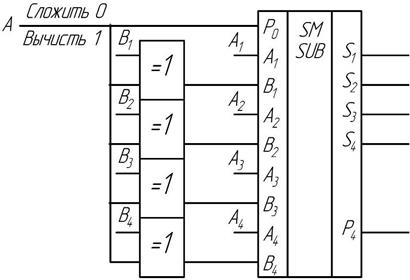
Рис. 2.21 Сумматор – вычитатель
В зависимости от сигнала на управляющем входе А «0» или «1» схемы «исключающее или» работают как повторители или инверторы слагаемого В = В4В3В2В1, поэтому вычитаемое предстает в прямом или обратном коде, а дополнительный код получается путем прибавления единицы на входе переноса, при Р0 = 1
Умножение и деление
Умножение сводится к операциям сдвига и сложения частных произведений.
Простейший перемножитель двоичных чисел это двухвходовой логический элемент И. Действительно, логическое перемножение входных переменных совпадает с арифметическим, т. к.
0 х 0 = 0
0 х 1 = 0
1 х 0 = 0
1 х 1 = 1
На рис. 2.22 приведена схема перемножителя двухразрядных двоичных чисел
А = А0 А1 и В = В0 В1.
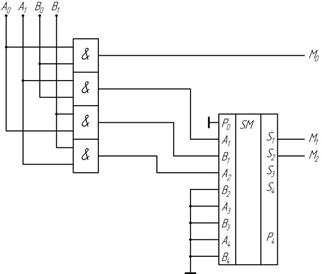
Рис. 2.22 Перемножитель двоичных чисел
Лекция 7
Компараторы
Компараторы – это устройства, предназначенные для сравнения кодов двух чисел. Схема простейшего компаратора двух чисел А и В приведена на рис. 2.23.
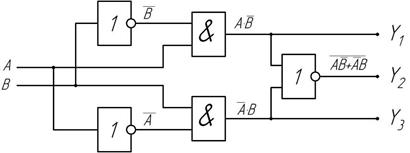
Рис. 2.23 Схема компаратора одноразрядных двоичных чисел
По существу это схема логического элемента «исключающее ИЛИ».
Заполним таблицу:
| Входы | Выходы | |||
| А | В | 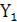
| 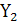
| 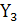
|
Из таблицы видно что:
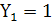 , если А
, если А 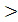 В
В
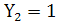 , если А
, если А 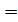 В
В
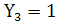 , если А
, если А 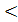 В
В
Если сравниваемые числа имеют несколько разрядов, необходимо сравнивать каждый разряд одного числа с тем же разрядом другого числа.
Например ИС К561ИП2 (рис. 2.24).
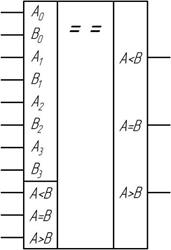
Рис. 2.24 Четырехразрядный компаратор К561ИП2
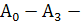 входы 4х разрядного числа А
входы 4х разрядного числа А
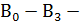 входы 4х разрядного числа В
входы 4х разрядного числа В
Входы А 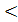 В, А
В, А 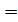 В, А
В, А 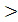 В – расширяющие входы на которые подают сигналы от предыдущих компараторов;
В – расширяющие входы на которые подают сигналы от предыдущих компараторов;
Выходы А 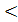 В , А
В , А 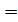 В, А
В, А 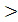 В предназначены для наращивания разрядности, их соединяют с одноименными входами последующих схем.
В предназначены для наращивания разрядности, их соединяют с одноименными входами последующих схем.
На рис. 2.25 приведена схема наращивания, позволяющая увеличить число разрядов сравниваемых слов до 12.
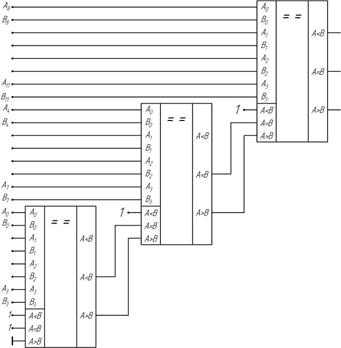
Рис. 2.25 Схема наращивания компараторов
Дата добавления: 2017-05-02; просмотров: 13080;











