МЕХАНИЧЕСКИЙ РАСЧЕТ МАГНИТОПРОВОДА РОТОРА
СИНХРОННОЙ МАШИНЫ
В синхронных машинах общего назначения мощностью свыше 100 кВт магнитопровод ротора имеет два вида исполнения. У быстроходных машин магнитопровод выполняется из отдельных дисков (рис. 8.42), которые затем стягиваются шпильками, либо заклепками, либо электросварочным швом. Полюсы к магнитопроводу крепятся с помощью хвостов. В тихоходных машинах ротор выполняется в виде магнитного колеса (рис. 8.43), к ободу которого шпильками прикрепляются полюсы.
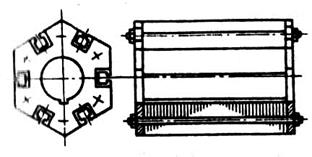
Рис. 8.42. Шихтованный ротор синхронной машины
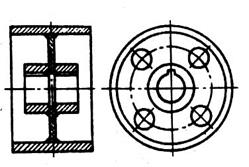
Рис. 8.43. Ротор синхронной машины
в виде сварного магнитного колеса
При вращении ротора его магнитопровод испытывает растягивающее напряжение центробежной силы, обусловленной собственной силой тяжести и силой тяжести прикрепленных к нему полюсов. Для того чтобы центробежная сила не вызывала остаточной деформации в магнитопроводе, необходимо, чтобы максимальные напряжения были меньше или равны допустимым. Напряжения в магнитопроводе ротора определяют из расчета его на прочность.
8.6.1. Расчет дискового ротора
Магнитопровод ротора можно разбить на две части: собственно магнитопровод, ограниченный внутренним отверстием вала радиусом 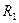 и окружностью радиусом
и окружностью радиусом 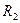 (до дна пазов), и хвостовую зону, ограниченную внешним контуром сердечника и окружностью радиусом
(до дна пазов), и хвостовую зону, ограниченную внешним контуром сердечника и окружностью радиусом 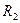 (см. рис. 8.34).
(см. рис. 8.34).
Масса хвостовой зоны на 1 м длины ротора, кг/м,
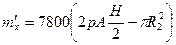 , (8.71)
, (8.71)
где 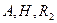 , м, — по рис. 8.34.
, м, — по рис. 8.34.
Центробежная сила хвостовой зоны на 1 м длины, Н/м,
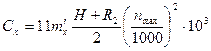 . (8.72)
. (8.72)
Центробежная сила полюса с обмоткой на 1 м длины, Н/м,
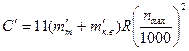 , (8.73)
, (8.73)
где 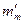 и
и 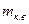 — массы полюса и катушки обмотки возбуждения на 1 м длины, кг/м, по (8.51) и (8.50);
— массы полюса и катушки обмотки возбуждения на 1 м длины, кг/м, по (8.51) и (8.50); 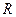 — средний радиус центра тяжести полюса, м.
— средний радиус центра тяжести полюса, м.
Радиальное напряжение на поверхности радиуса 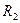 , Па,
, Па,
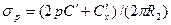 . (8.74)
. (8.74)
Максимальное тангенциальное напряжение, которое возникает на внутренней поверхности магнитопровода радиусом 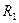 , Па,
, Па,
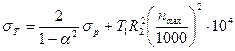 , (8.75)
, (8.75)
где 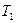 — коэффициент, определяемый в зависимости от отношения
— коэффициент, определяемый в зависимости от отношения 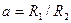 по следующей формуле:
по следующей формуле:
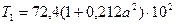 . (8.76)
. (8.76)
Тангенциальное напряжение в стали магнитопровода ротора с учетом ослабления шпоночной канавкой, Па,
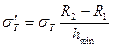 . (8.77)
. (8.77)
Если в магнитопроводе имеется отверстие для стяжной шпильки, то из 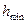 следует вычесть диаметр этого отверстия. Напряжение в стали магнитопровода
следует вычесть диаметр этого отверстия. Напряжение в стали магнитопровода 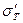 не должно превышать 130 МПа.
не должно превышать 130 МПа.
Пример.Исходные данные: 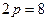 ,
, 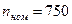 об/мин,
об/мин, 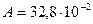 м,
м, 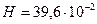 м,
м, 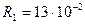 м,
м, 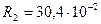 м,
м, 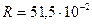 м,
м, 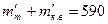 кг/м,
кг/м, 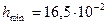 м.
м.
Из (8.71)
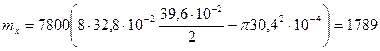 кг/м;
кг/м;
по (8.72)
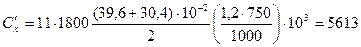 Н/м;
Н/м;
по (8.73)
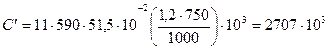 Н/м.
Н/м.
Радиальное напряжение по (8.74)
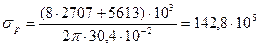 Па.
Па.
По (8.76)
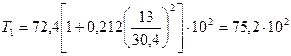 .
.
Тангенциальное напряжение по (8.75) и (8.77)
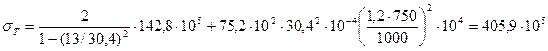 Па;
Па;
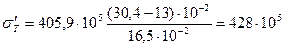 Па.
Па.
8.6.2. Расчет ротора в виде магнитного колеса
Магнитное колесо представляет собой сварную конструкцию, состоящую из стальной втулки, насаживаемой на вал, обода, к которому прикрепляются полюсы, и диска, соединяющего втулку и обод. Иногда в диске делают отверстия, между которыми образуются своеобразные спицы (рис. 8.44).
Центробежная сила обода, Н,
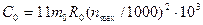 , (8.78)
, (8.78)
где 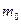 — масса обода, кг:
— масса обода, кг:
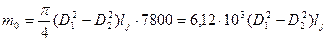 ; (8.79)
; (8.79)
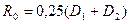 — средний радиус обода, м.
— средний радиус обода, м.
Центробежная сила полюсов с обмотками, Н,
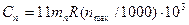 , (8.80)
, (8.80)
где 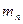 — масса всех полюсов с обмотками, кг:
— масса всех полюсов с обмотками, кг:
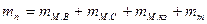 . (8.81)
. (8.81)
Массы 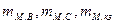 и
и 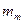 определяют из электромагнитного расчета по (10.150)—(10.153);
определяют из электромагнитного расчета по (10.150)—(10.153); 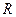 — радиус центра тяжести полюса с обмотками, м, по (8.49).
— радиус центра тяжести полюса с обмотками, м, по (8.49).
Сила, растягивающая втулку, Н,
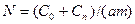 , (8.82)
, (8.82)
где 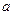 — расчетный коэффициент:
— расчетный коэффициент:
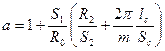 ; (8.83)
; (8.83)
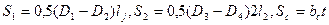 — площади сечения обода, втулки, спицы, м2;
— площади сечения обода, втулки, спицы, м2; 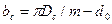 — расчетная ширина спицы, м;
— расчетная ширина спицы, м; 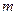 — число спиц;
— число спиц; 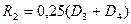 — средний радиус втулки;
— средний радиус втулки; 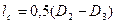 — длина спицы;
— длина спицы; 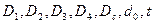 — размеры, м, по рис. 8.44.
— размеры, м, по рис. 8.44.
Сила, передаваемая на втулку, Н,
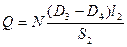 . (8.84)
. (8.84)
Напряжения при максимальной частоте вращения, Па:
в ободе на растяжение без учета спиц
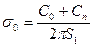 ; (8.85)
; (8.85)
во втулке
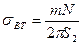 ; (8.86)
; (8.86)
в швах А
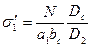 ; (8.87)
; (8.87)
в швах Б
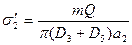 ,
,
где 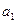 и
и 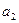 — размеры сварочных швов А и Б, м (рис. 8.44).
— размеры сварочных швов А и Б, м (рис. 8.44).
Можно принять
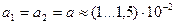 м. (8.88)
м. (8.88)
Напряжения при номинальной частоте вращения в швах Б, Па:
на растяжение
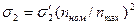 ; (8.89)
; (8.89)
на срез
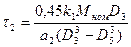 , (8.90)
, (8.90)
где 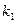 — коэффициент перегрузки;
— коэффициент перегрузки; 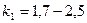 ;
;
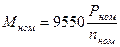 ;
;
на срез (приведенное)
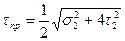 . (8.91)
. (8.91)
Допустимые напряжения в ободе и втулке принимают равными до 100 МПа, в швах на растяжение 80 МПа, на срез 45 МПа.
Пример.Исходные данные: 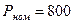 кВт,
кВт, 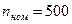 об/мин,
об/мин, 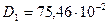 м,
м, 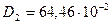 м,
м, 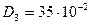 м,
м, 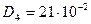 м,
м, 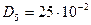 м,
м, 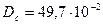 м,
м, 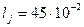 м,
м, 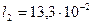 м,
м, 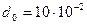 м,
м, 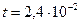 м,
м, 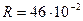 м,
м, 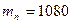 кг;
кг; 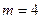 .
.
Последовательно применяя (8.78)—(8.91), получаем
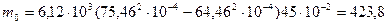 кг;
кг;
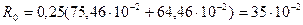 м;
м;
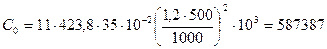 Н;
Н;
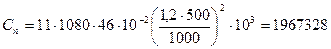 Н;
Н;
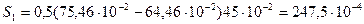 м2;
м2;
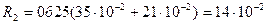 м;
м;
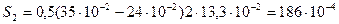 м2;
м2;
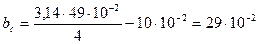 м;
м;
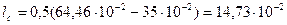 м;
м;
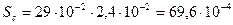 м2;
м2;
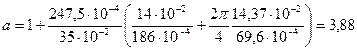 ;
;
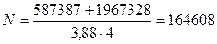 Н;
Н;
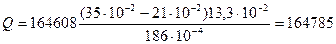 Н;
Н;
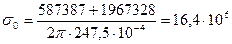 Па;
Па;
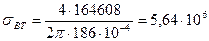 Па;
Па;

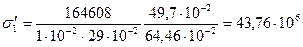 Па;
Па;
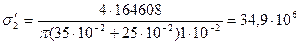 Па;
Па;
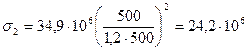 Па;
Па;
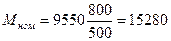 Н·м;
Н·м;
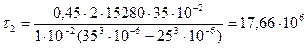 ;
;
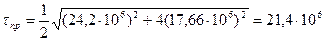 Па.
Па.
Все напряжения находятся в допустимых пределах.
| <== предыдущая лекция | | | следующая лекция ==> |
| | |
Дата добавления: 2017-05-02; просмотров: 1240;











