Приток жидкости к наклонным и многозабойным скважинам в слоистом пласте

Исследование притока жидкости к многозабойным и горизонтальным скважинам приводит к постановке весьма сложных пространственных задач подземной гидродинамики. Однако во многих случаях пластовые условия позволяют упростить постановку задач и свести их к решению соответствующих плоских задач.

Предположим, что течение жидкости в пласте послой­ное. Довольно часто в мощном и сравнительно хорошо проницаемом пласте при тщательном анализе обнаруживается существование относительно тонких плохопроницаемых пропластков. Особенности обводнения скважин, перемещении контура нефте­носности и фронта закачки воды в пласт доказывают, что между соседними проницаемыми пропластками вблизи скважины перетока нет.

При условиях, когда мощности разделяемых пропластков не­велики, жидкость движется вдоль поверхностей напластования. При небольших углах наклона и при большой протяженности пласта вполне допустимо движение жидкости рассматривать как плоское движение, то есть можно пренебречь составляющей скорости движения жидкости в направлении, перпендикулярном к поверхности напла­стования. Чем меньше мощность пласта или чем больше в нем слабо­проницаемых тонких прослоев, тем точнее будет высказанное до­пущение.

Рассмотрим простейшие условия притока жидкости многозабойной скважине в условиях водонапорного режима. Считаем, что горизонтальный слоистый пласт постоянной мощ­ности h насыщен однородной несжимаемой жидкостью с постоянной вязкостью.

При дальнейших расчетах и выводах будем исходить из предположения, что вертикальная проницаемость пласта равна нулю. В этом случае весь поток разбивается на ряд плоских бесконечно малых потоков в слоях бесконечно малой мощности. Проницаемость в горизонтальном направлении принимаем постоянной. Рассмотрим приток нефти к одиночным многозабойно- горизонтальным скважинам и к системам их в круговой и полосообразной залежах.

Многозабойная скважина без центрального работающего ствола. Под многозабойной скважиной понимаем скважину, n стволов которой размещены равномерно по поверхности конуса с вершиной в кровле пласта и наклонены под равными углами и от вертикали. Приток через центральный ствол отсутствует. Он служит только для удобства эксплуатации многозабойной сква­жины.

Формулу для определения притока жид­кости к многозабойной скважине получаем как частный случай формулы для определе­ния притока жидкости к батарее наклонных скважин.

Если радиус батареи наклон­ных скважин по кровле пласта r_*, по подошве 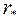, то при стремлении r_* к нулю, батарея наклонных скважин превращается в многозабойную скважину с n стволами (рис. 1.1).

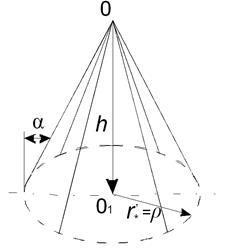
Рис. 1.1. Многозабойная скважина

Выражение для подсчета дебита мно­гозабойной скважины имеет вид [23]:

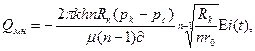(1.1)

где Еi (t) - интегральная экспоненциальная функция, h - толщина пласта, n - число стволов скважины, 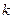- проницаемость пласта, 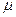- вязкость жидкости, 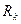- радиус контура питания, 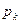- среднее значение пластового давления на контуре питания, 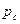- забойное давление, 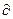- длина проекции ствола наклонной скважины на подошву,

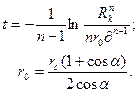(1.2)

Здесь 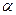- угол наклона отдельного ствола многозабойной скважины от вертикали, r_c - радиус скважины.

Эффективность многозабойной скважины по сравнению с вертикальной определяется из отношения 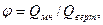где 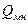- дебит многозабойной скважины, 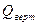- дебит вертикальной скважины.

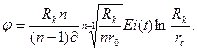(1.3)

Во ВНИИ по формулам (1.1) и (1.3) произведены расчеты притока нефти к одиночной многозабойной скважине для различного количества стволов n, различных углов наклона стволов от вертикали 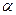, различных значений 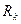и двух значе­ний h. Результаты исследования показали, что от многозабойной скважины можно ожидать значительный эффект. При малых 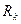(200 - 500 м), что может иметь место при осуществлении заводнения, дебит многозабойной скважины может быть больше дебита вертикальной скважины в 10 раз и более при n=4 и 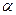>45°. Для наиболее вероятного значения 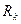> 1000 м, n=4 и 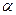>45° не следует ожидать в условиях слоистого пласта превышения дебита многозабойной скважины над дебитом вертикальной более чем в 4 раза [26, 27] .

Расстояние до контура питания при прочих равных условиях
существенно влияет на дебит многозабойной скважины при малых его значениях. При больших 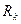, малых углах наклона и малом
числе стволов превышение дебита многозабойной скважины над
дебитом вертикальной скважины мало, ввиду значительного превышения внешних фильтрационных сопротивлений над внутренними.

При n > 6 дебит возрастает очень медленно. Практически нецелесообразно бурить более четырех стволов в многозабойной скважине. Когда дополнительная добыча от введения в работу но­вого ствола не будет окупать его проходку, то количество пробу­ренных стволов многозабойной скважины будет считаться их пре­делом.

Многозабойная скважина с центральным вертикальным стволом.Положим теперь, что жидкость фильтруется через наклонные стволы и через вертикальный ствол в пределах продуктив­ной части пласта (рис. 1.2).

Для определения дебита многозабойной скважины с работаю­щим центральным стволом найдем элементарный приток в отдельном слое и просуммируем его по мощности от 0 до h.

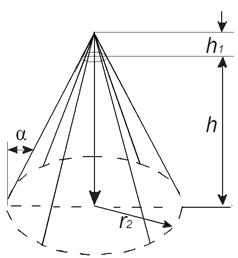
Рис. 1.2. Многозабойная скважина с центральным стволом

Тогда получим выражение вида 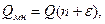где

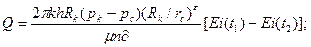
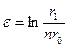. (1.4)

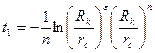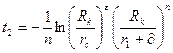, , (1.5)

r₁ - расстояние от центрального ствола до точек входа в пласт наклонных стволов, r₂ =r₁ + 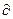- расстояние по подошве пласта от центрального ствола до точек выхода наклонных стволов из пласта.

При 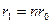дебит центрального ствола становится равным нулю. Поэтому высота забуривания стволов от кровли пласта должна быть .

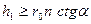Приведем приближенные простые и более удобные для расчета формулы, обеспечивающих в то же время необходимую точность, как для одиночных скважин, так и для их систем.

Положим, что слоистый пласт конечной толщины h разрабаты­вается системами батарей из n наклонных или многозабойных сква­жин. Стволы пересекают пласт на всю толщину от кровли до подошвы. Проницаемость пласта по вертикали равна нулю, по гори­зонтали постоянна и равна k.

В слоистом пласте каждый наклонный ствол в каждом слое представляет собой эллиптическую скважину, но в разных слоях их положение различно, и полный дебит наклонного ствола или какой-либо совокупности наклонных стволов определяется сумми­рованием дебитов по отдельным слоям.

В ряде случаев такое суммирование осуществить трудно. Если же и удается суммировать дебиты, то получаются довольно громозд­кие расчетные формулы.

Известно, что небольшое изменение местоположения взаимодействующих скважин незначительно сказывается на их суммарном дебите. Это позволяет взять для всех слоев одинаковое положение сечений наклонных стволов, соответствующее действительному положению этих сечений в каком-то одном слое. Всегда можно найти слой со средним значением дебита, изме­няющегося по толщине пласта. Если взять за такой основной (базисный) слой средний, равноуда­ленный от кровли и подошвы пласта, то полученные при этом фор­мулы будут вполне пригодными для практических расчетов.

Формула для опре­деления притока жидкости к многозабойной скважине с т забоями (стволами), размещенными равномерно по поверхности конуса выглядит следующим образом:

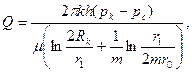(1.6)

где r₁ – длина одного ствола на кровлю или подошву пласта, r₀ – радиус круговой скважины эквивалентной по дебиту эллиптической скважине, определяемый по формуле

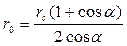, (1.7)

r_c – действительный радиус ствола скважины.

Если наклонные стволы забуривают выше кровли пласта, используют следующую формулу:

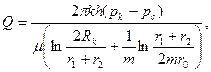(1.8)

где r₁ и r₂ – радиус батареи по подошве и кровле пласта, (r₁+r₂)/2 – радиус в среднем слое.

Определение притока многозабойных скважин в тонком пласте [27].Рассмотрим три случая, когда скважины в пласте имеют вид креста, звезды и линии [28].

Полагаем, что длины отдельных лучей одинаковы и равны а. Интенсивность притока к каждой точке рассматриваемой скважины считаем постоянной. На круговом контуре питания радиуса R_к считаем известным среднее значение пластового давлении. За давле­ние на скважине принимаем среднее значение давления на отдель­ном луче р_с.

Течение к крестообразной скважине в плоскости (рис. 1.3) определяется комплексным потенциалом

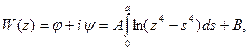(1.9)

где 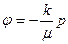- потенциал скорости, 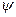- функция тока.

Рис. 1.3. Четырехзабойная скважина в плоском пласте

Приток пластовой жидкости на еди­ницу толщины пласта определяем при помощи контурного интеграла:

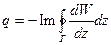. (1.10)

Давление на контуре питания определяем из зависимости:

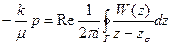. (1.11)

Среднее забойное давление на отдельном луче рассчитываем по формуле:

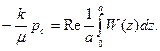(1.12)

С учетом приведенных выше зависимостей после некоторых преобразований суммарный дебит крестообразной скважины находим в виде:

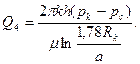(1.13)

При тех же условиях получаем приток к звездообразной скважине (рис. 1.4).

Течение к такой скважине в каждом слое определяется комплексным потенциалом:

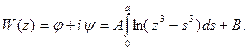(1.14)

Рис. 1.4. Трехзабойная скважина в плоском пласте

После преобразований, аналогичных тем, которые проведены в предыдущей задаче, получим выражение суммарного дебита звездо­образной скважины:

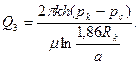(1.15)

Дебит скважины длиной 2а (рис. 1.5) определяем как предель­ный в задаче об установившемся притоке несжимаемой жидкости к эллиптической скважине с полуосями а и b при условии, что b стремится к нулю.

Рис. 1.5. Двухзабойная скважина в плоском пласте

Выражение для определения суммарного дебита горизонтальной скважины длиной 2а принимает вид

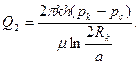(1.16)

Для скважины длиной a, вскрывшей пласт на полную толщину h от кровли до подошвы, выражение суммарного дебита имеет вид:

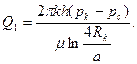(1.17)

Полученные выражения суммарных дебитов дают, очевидно, значения суммарных дебитов вертикальных трещин соответствующей формы.