Подобие гидродинамических явлений

Решение системы Навье-Стокса даже для простых задач представляет значительную сложность, поэтому большое значение приобретает гидродинамический эксперимент, вопросы моделирования процесса. При моделировании необходимо учитывать влияние большого количества факторов на протекание процесса, чтобы полученные результаты на моделях можно было переносить на действующие образцы. Эту сложность в значительной степени позволяет устранить теория подобия, которая утверждает, что влияние отдельных факторов можно рассматривать в совокупности объединяя их в безразмерные комплексы – критерии подобия. Эти критерии получаются путем перевода размерных уравнений движения в безразмерные. Все критерии имеют определенный физический смысл. Анализ задачи приобретает следующие особенности: 1) уменьшается число переменных, т.к. количество критериев всегда меньше количества образующих их величин; 2) ярче выделяются физические особенности рассматриваемой задачи; 3)анализ приобретает обобщенный характер, т.к. одно и то же значение комплекса может быть получено путем бесконечного варьирования образующих величин.

Гидродинамические явления будут подобными если течения протекают в геометрически подобных системах. Наблюдается подобие полей скоростей и других важных физических характеристик. Константы пропорциональности называются константами подобия.

Выясним условия, при которых течения описываемые системой Навье-Стокса будут подобными. По геометрическим условиям однозначности должен быть задан какой-то характерный линейный размер:

1) 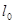; 2) по физическим условиям однозначности должны быть определены 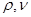; 3) по граничным условиям должна быть определена 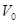; 4) по начальным условиям задано характерное время 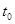, например период определяющий темп внешних воздействий

Таким образом в уравнениях зависимые переменные определяются как функции независимых переменных x, y, z, t и параметров задающих условие однозначности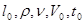

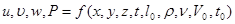
Приведем уравнение движения к безразмерному виду методом масштабных преобразований. Будем относить физические величины к одномерным параметрам

; ;

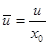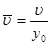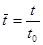
В качестве масштаба для массовых сил примем ускорение свободного падения.

; ; ;

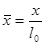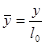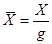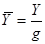
Выразим размерные величины через их масштабы в Уравнении Навье-Стокса:

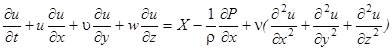
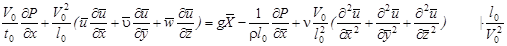
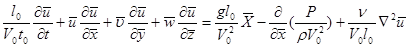
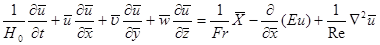
Аналогично могут быть получены составляющие системы уравнений вдоль оси у и z.

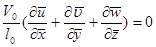
Уравнение сплошности после приведения к безразмерному виду не изменится. После приведения уравнения движения к безразмерному виду появились безразмерные комплексы.

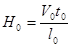- критерий динамической гомохронности;

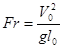- критерий Фруда;

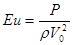- число Эйлера; 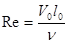- критерий Рейнольдса.

После приведения уравнений к безразмерному виду изменился их физический смысл, т.к. один и тот же вид уравнений с подобными условиями будут соответствовать не единственному условию, а целой группе подобных явлений. В соответствии с теоремой подобия Кирпичева-Гухмана гидродинамические явления будут подобными если они: 1) описываются одной системой дифуравнений; 2) имеют подобные условия однозначности; 3) имеют численно равные критерии подобия