методы определения константы михаэлиса и максимальной скорости процесса
Существует несколько методов определения параметров уравнения Михаэлиса-Ментен (константы Михаэлиса и максимальной скорости реакции) для односубстратной реакции. Наиболее распространенный из них – линеаризация уравнения Михаэлиса-Ментен. Полный анализ включает определение не только Vmax и KM, но и KS, k1, k-1, k2.
Из кривой, построенной на основе исходного уравнения Михаэлиса-Ментен, можно определить графическим методом значения констант Vmax и KM, но это неудобно, так как невозможно провести асимптоту к гиперболе с хорошей точностью.
Первый способ линеаризации был описан Холдейном и Штерном в их учебнике по энзимологии. Для осуществления такого преобразования уравнение Михаэлиса-Ментен представляют в двойных обратных координатах, то есть, единицу делят на V0 и переворачивают дробь в правой части уравнения:
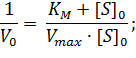
| (1) |
Преобразовав уравнение (1), получаем один из часто применяемых способов линеаризации – уравнение Лайнуивера-Берка:
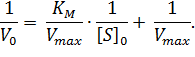
| (2) |
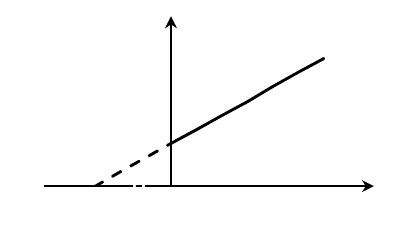
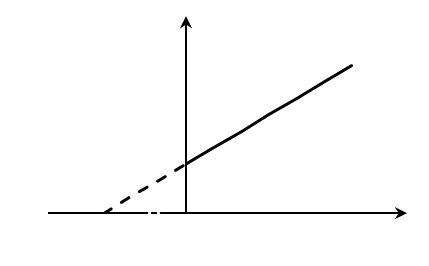
При построении зависимости в двойных обратных координатах, 1/V0 от 1/[S]0, как показано на рисунке 1, получаем прямую. Из уравнения линейной регрессии можно определить интересующие константы.
 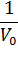 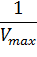 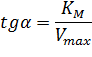 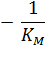 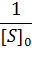
| |||
| Рисунок 1 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Лайнуивера-Берка. |
Отсекаемый отрезок на оси ординат дает обратную максимальную скорость, а на оси абсцисс – обратную константу Михаэлиса с противоположным знаком. Или же определяют непосредственно из уравнения прямой обратную максимальную скорость, а потом константу Михаэлиса из тангенса угла наклона прямой (рисунок 1).
Точность определения кинетических параметров таким способом считается невысокой. Чем меньше концентрация субстрата, тем выше оказывается ошибка определения обратной скорости.
Домножив обе части уравнения (2) на начальную концентрацию субстрата [S]0, получаем уравнение Хейнса:
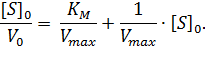
| (3) |
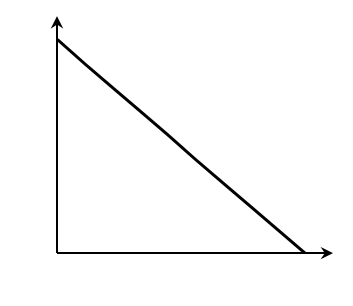
Построив зависимость [S]0/V0 от [S]0, как показано на рисунке 2, получим прямую, из уравнения линейной регрессии которой можно определить параметры Vmax и KM.
| 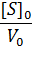 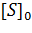 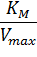 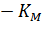 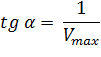
| |||
| Рисунок 2 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Хейнса. |
Существует еще один вариант преобразования уравнения Михаэлиса-Ментен. Для его осуществления избавляются от знаменателя, умножив на него обе части исходного уравнения и делят обе части на 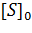 :
:
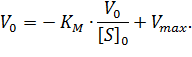
| (4) |
Мы получили уравнение Иди-Хофсти. Его графиком является прямая в координатах V0 от [S]0/V0, из уравнения линейной регрессии которой можно определить те же кинетические параметры - Vmax и KM в соответствии с рисунком 3.
| 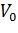 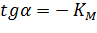 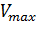 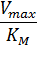 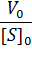
| |||
| Рисунок 3 – Зависимость начальной скорости реакции от начальной концентрации субстрата в координатах уравнения Иди-Хофсти. |
Статистический анализ показывает, что методы Хейнса и Иди-Хофсти дают более точные результаты, чем метод Лайнуивера-Берка. Причиной этого является то, что в первых двух графиках и зависимые, и независимые переменные входят в величины, откладываемые на обеих осях координат.
Нередко наблюдается спрямление экспериментальных данных в координатах уравнения Лайнуивера-Берка и невозможность такого преобразования по остальным уравнениям. Это говорит о том, что результаты, полученные посредством одной линеаризации, не слишком надежды и необходимо применять все три одновременно.
Очень точный графический метод – «прямой график» Эйзенталя-Боудена. Каждой начальной концентрации субстрата [S]i соответствует значение начальной скорости Vi (i = 1,2,…n). Значения [S]i с обратным знаком откладываются на оси абсцисс, на оси ординат – значения Vi. Через полученные пары точек проводят прямые, пересекающие координатные оси в точках (-[S]i, 0) и (0, Vi). Проекция общей точки пересечения прямых на горизонтальную ось равна КМ, а на вертикальную – Vmax (рисунок 4).
Разброс экспериментальных данных в этом методе учитывают с помощью нахождения медианы (в случае непрерывных распределений медианой является место, выше и ниже которого находится по 50% экспериментальных значений; другими словами, значения, лежащие ниже и выше медианы, встречаются с вероятностью 0,5).
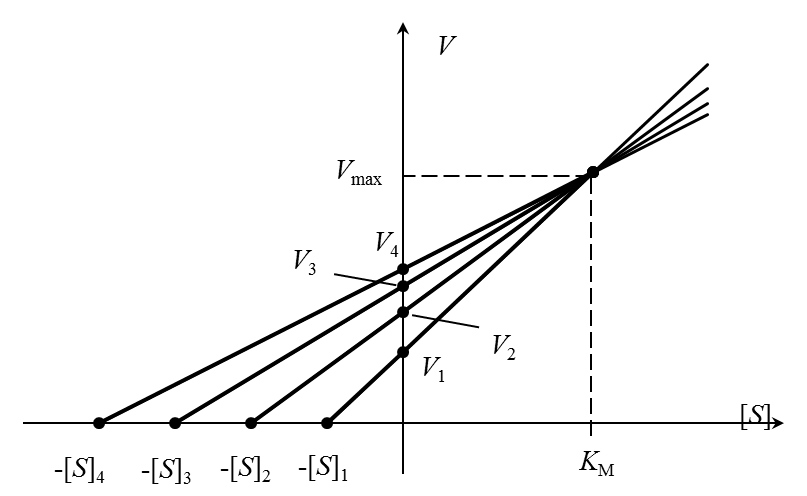
|
| Рисунок 4 – Определение констант уравнения Михаэлиса-Ментен по методу Корниш-Боудена. |
Для определения максимальной скорости и константы Михаэлиса применяют также метод Диксона, согласно которому точку начала координат соединяют прямыми линиями с точками на кривой уравнения Михаэлиса-Ментен, соответствующими значениям 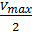 ,
, 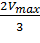 ,
, 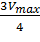 , … Прямые отсекают на горизонтальной линии
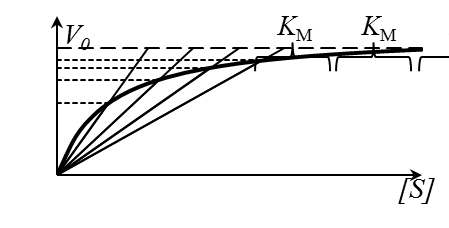
, … Прямые отсекают на горизонтальной линии 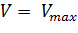 одинаковые отрезки, длина которых равна КМ (рисунок 5). То есть, метод предполагает, что величина
одинаковые отрезки, длина которых равна КМ (рисунок 5). То есть, метод предполагает, что величина 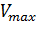 определена. Следует отметить, что отсекаемые отрезки одинаковы только в том случае, если
определена. Следует отметить, что отсекаемые отрезки одинаковы только в том случае, если 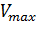 определена верно (рассчитанное каким-то другим методом значение максимальной скорости близко к истинному). Если это не так, будут наблюдаться расхождения:
определена верно (рассчитанное каким-то другим методом значение максимальной скорости близко к истинному). Если это не так, будут наблюдаться расхождения:
- если рассчитанная 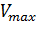 меньше истинного значения, то с увеличением начальной концентрации субстрата значения КМ монотонно убывают;
меньше истинного значения, то с увеличением начальной концентрации субстрата значения КМ монотонно убывают;
- если рассчитанная 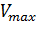 больше истинной, то с увеличением начальной концентрации субстрата определяемые значения
больше истинной, то с увеличением начальной концентрации субстрата определяемые значения 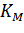 монотонно возрастают.
монотонно возрастают.
То есть, метод позволяет установить точность определения 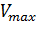 .
.
 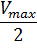 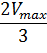 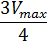 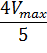
|
| Рисунок 5 – Определение КМ по методу Диксона. |
Анализируя графическим методом, проведем касательную к кривой в координатах уравнения Михаэлиса-Ментен. Для этого необходимо продифференцировать уравнение и подставить в полученную функцию значение концентрации в той точке, касательная к которой необходима – это точка (0;0), так что 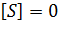 . В результате получаем угловой коэффициент касательной. Зная его и одну точку прямой (точка (0;0)), строим касательную и продляем до горизонтальной линии
. В результате получаем угловой коэффициент касательной. Зная его и одну точку прямой (точка (0;0)), строим касательную и продляем до горизонтальной линии 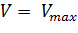 . В том случае, если начальная концентрация субстрата очень велика по сравнению с концентрацией фермента (
. В том случае, если начальная концентрация субстрата очень велика по сравнению с концентрацией фермента ( 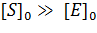 ), расстояние между касательной (горизонтальная линия
), расстояние между касательной (горизонтальная линия 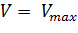 ) к кривой в координатах уравнения Михаэлиса-Ментен при
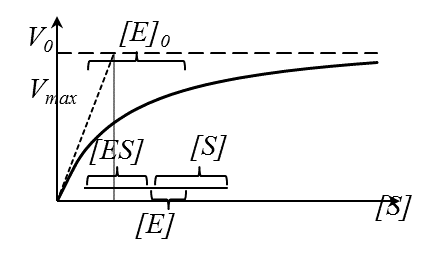
) к кривой в координатах уравнения Михаэлиса-Ментен при 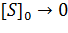 и осью ординат также равно КМ. Если оно оказывается больше КМ, то концентрацией фермент-субстратного комплекса [ES] нельзя пренебречь и можно определить графически значения [ES], [E] и [S] в каждой точке этой кривой. Если провести прямую, параллельную оси абсцисс, отрезок между осью ординат и касательной будет численно равен концентрации фермент-субстратного комплекса, а отрезок между касательной и перпендикуляром на ось абсцисс из точки пересечения касательной с прямой
и осью ординат также равно КМ. Если оно оказывается больше КМ, то концентрацией фермент-субстратного комплекса [ES] нельзя пренебречь и можно определить графически значения [ES], [E] и [S] в каждой точке этой кривой. Если провести прямую, параллельную оси абсцисс, отрезок между осью ординат и касательной будет численно равен концентрации фермент-субстратного комплекса, а отрезок между касательной и перпендикуляром на ось абсцисс из точки пересечения касательной с прямой 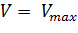 - концентрации свободного фермента [E]. Длина отрезка между кривой Михаэлиса-Ментен и касательной дает значение концентрации субстрата в этой же точке (рисунок 6).
- концентрации свободного фермента [E]. Длина отрезка между кривой Михаэлиса-Ментен и касательной дает значение концентрации субстрата в этой же точке (рисунок 6).
|
| Рисунок 6 – Графический метод определения концентраций свободных фермента и субстрата, а также концентрации фермент-субстратного комплекса. |
| <== предыдущая лекция | | | следующая лекция ==> |
| Промышленном водоснабжении | | | Состав и характеристики пропульсивного комплекса. |
Дата добавления: 2021-07-22; просмотров: 886;