Горизонтальная структура геологических тел

Под горизонтальным понимается такое залегание геологических тел, которое характеризуется углами наклона (падения), измеряемыми минутами и первыми (1-2) градусами. Идеально горизонтальные поверхности можно рассматривать как исключения и частные случаи, принимая во внимание их исключительную редкость. Горизонтальным залеганием могут обладать любые тела и поверхности раздела геологических тел – от наиболее часто встречающихся поверхностей напластования (не обязательно находящихся в первичном залегании) до границ магматических тел, трещин и сместителей разрывных нарушений. Определяющей характеристикой горизонтальной структуры является приблизительное (в разумных пределах, учитывая масштаб рассмотрения и изображения) равенство абсолютных отметок граничных поверхностей. Конфигурация границ тел на карте при этом целиком диктуется рельефом местности, повторяя в том или ином приближении рисунок изогипс (горизонталей) рельефа. На картах, где рельеф передается с помощью горизонталей, границы горизонтально залегающих геологических тел не могут пересекать эти последние. Напротив, пересечение границ и изогипс рельефа свидетельствует о наклонном залегании поверхностей раздела и самих тел. Определяющая роль рельефа в изображении горизонтально залегающих тел хорошо просматривается на приводимой схеме (рис. 2.1-1): границы полностью «вписываются» в рисунок горизонталей, ширина выхода зависит от крутизны склона (а не только от мощности).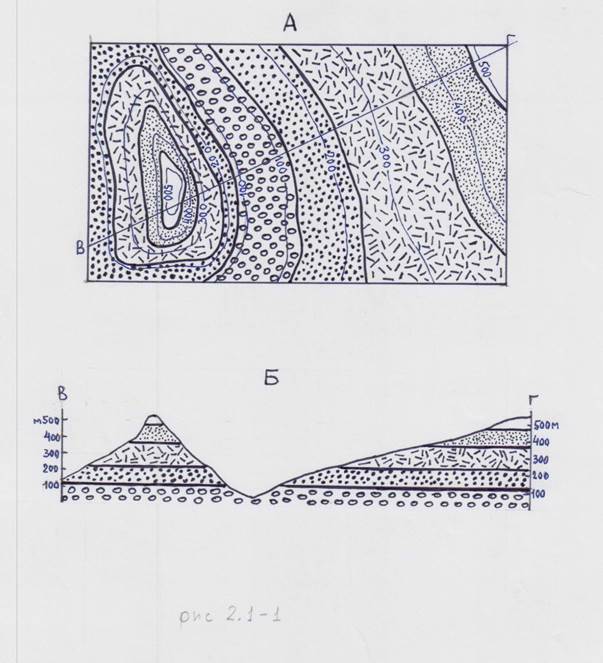

Рис. 2.1-1 Горизонтальная структура: А – в плане (на карте), Б – в разрезе. Видна зависимость ширины выхода тела (слоя) от наклона земной поверхности.

Мощность горизонтально залегающих тел (слоев) определяется либо по разнице абсолютных отметок кровли и подошвы, либо графически (по замеренной ширине выхода и углу склона), либо математически (рис.2.1-2).

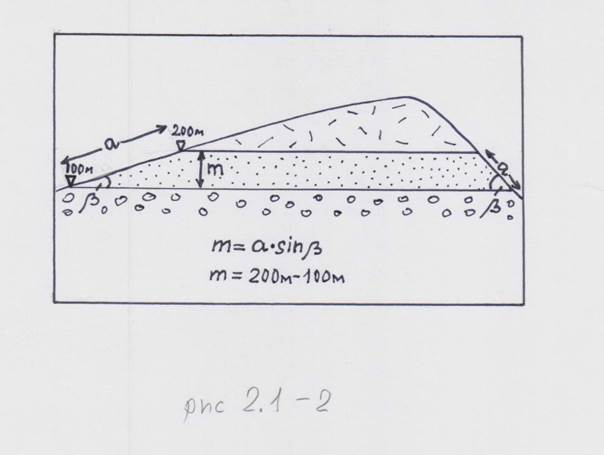
Рис. 2.1-2 Схема, поясняющая определение мощности горизонтально залегающего слоя. (m – мощность слоя, a – ширина выхода на склоне, бета – угол склона).

Пояснений требует поведение границ (точнее, их изображение на геологических картах) на вертикальных (или близких к таковому) склонах. Естественно, что на картах границы здесь сливаются, что зрительно приводит к впечатлению о пересечении геологических границ, однозначно трактуемое как несогласное залегание (срезание, секущий интрузивный контакт и т.п.), чего на самом деле нет. Для того чтобы избежать возможных неверных трактовок в подобных случаях, необходимо сохранить все границы на этом склоне, «разведя» их на технически выполнимое расстояние (1-2 мм), несколько нарушив при этом «картографическую логику». При этом придется на карте сдвинуть границы с мест их наблюдаемого выхода на поверхность. Однако эта «потеря», несомненно, менее значима, чем появление несуществующего в действительности несогласия, могущего изменить представление о реальном ходе геологической истории изучаемого региона.

По тем картам, где отсутствует горизонтали – чаще всего это обзорные региональные карты – суждение о горизонтальности – не горизонтальности залегания геологических тел затруднено, и в общем случае имеет предположительный характер. Однако даже на таких картах обязательно показана гидрографическая сеть (реки, временные водотоки, озера и т.п.). Естественно, что в этом случае геологические границы будут повторять в общих чертах узор этой сети (рис 2.1-3), выполняя роль горизонталей рельефа.

Рис 2.1-3 Выражение горизонтальной структуры на карте без горизонталей рельефа.

При этом, правда, остается возможность ошибки, т.к. при слабо наклонном залегании конфигурация границ не будет принципиально отличаться от таковой при горизонтальном положении границ раздела.

Важной особенностью горизонтальной структуры (при надежном определении кровли – подошвы пластов) является простое определение стратиграфической последовательности: гипсометрически выше расположенные пласты моложе обнажающихся на более низких абсолютных отметках, а водоразделительные пространства сложены наиболее молодыми породами, напротив, выходящие у уреза воды пласты являются наиболее древними.

Горизонтальные структуры в наибольшей степени свойственны платформенным областям и другим крупным геологическим объектам, в строении которых принимают участие недислоцированные или слабо дислоцированные покровные чехлы (срединные массивы, приплатформенные участки краевых прогибов и т.п.)

При построении разрезов горизонтальной структуры допустимо изменение вертикального масштаба. Это обстоятельство связано с тем, что мощности стратиграфических подразделений на платформах очень часто невелики и не могут быть выражены в масштабе карты. Для определения минимально необходимого вертикального масштаба используют мощность самого маломощного из показанных на карте слоев, считая, что она может быть выражена технически выполнимым отрезком в 1 мм. Например, на геологической карте масштаба 1:200000 самый маломощный слой из изображенных имеет мощность 10 м. Примем, что эти 10 м могут быть изображены 1 мм, тогда вертикальный масштаб будет: (в 1 мм – 10 м, или 10000 мм), 1:10000, т.е. вертикальный масштаб, принятый по этой схеме, в 20 раз крупнее горизонтального. Допустимо преувеличение в 40 раз, но при этом резко возрастает цена любой неточности, как в плане, так и в разрезе, что чревато искажениями геологической ситуации. Нормальным же является соотношение вертикального и горизонтального масштабов равное 1:1, отсюда преувеличение должно быть минимально необходимым.

2.2 Моноклинальная структура

Наклонное залегание – это наиболее распространенный вид нахождения геологических тел в природе. Теоретически рассуждая, наклонным следует считать любое не горизонтальное (угол наклона равен 0) и не вертикальное (угол с горизонтом 90) залегание геологических тел. Естественно, что большинство тел характеризуется как раз таким наклонным или моноклинальным залеганием.

Для определения положения наклонно залегающих тел в пространстве используются элементы залегания, определяемые непосредственно с помощью горного компаса (см. выше, глава …). Минимально необходимы азимут падения и угол падения. Однако прямое определение этих элементов горным компасом возможно далеко не всегда. При определенных условиях приходится прибегать к графическим построениям.

Наиболее общий метод непрямого определения элементов залегания заключается в следующем. Для решения задачи необходимо знать пространственное положение и абсолютную высоту в трех точках одной и той же геологической поверхности: кровли или подошвы пласта, трещины, сместителя, поверхности плоского магматического тела (дайки) и т.п. На геологической (или топографической) карте (рис.2.2-1)

в точках А, Б, и В установлена подошва одного и того же пласта и ее абсолютные высоты.

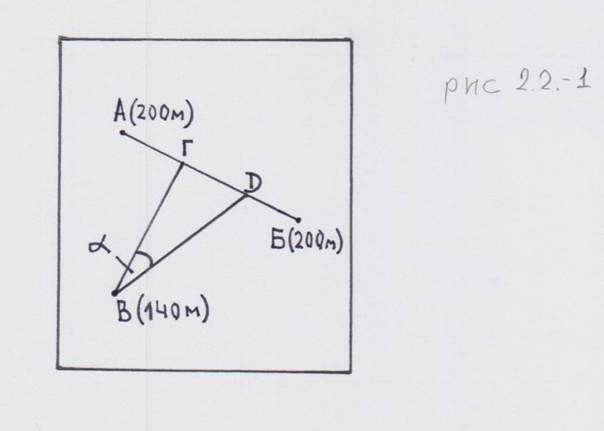
Рис.2.2-1 Определение элементов залегания по трем точкам. Масштаб – 1:4000.

Абсолютные отметки могут быть получены либо при непосредственном наблюдении на местности, либо в скважинах, либо геофизическими методами (напр. ВЭЗ – вертикальное электрозондирование). Возможны три варианта: 1) абсолютные отметки во всех точках равны (А=Б=В); 2) они же равны в двух точках (А=Б>В), 3) во всех точках абсолютные отметки различны (А>Б>В).

Первый вариант – пласт залегает горизонтально. Через три точки можно провести только одну плоскость, а если абсолютные высоты этих точек равны, то плоскость – горизонтальна.

Во втором случае (рис. 2.2-1): соединяем точки А и Б прямой, по определению – это линия простирания, следовательно перпендикуляр ВГ, опущенный из точки В на эту линию (или ее продолжение) – линия падения, точнее ее проекция на плоскость карты, (по определению линия падения наклонна), азимут которой легко измеряется. Для определения угла падения на линии простирания от точки ее пересечения с линией падения (Г) откладывается в масштабе карты разница высот точек А (Б) и В. Полученная точка D соединяется с В, при которой и возникает угол падения (если треугольник ВГD поставить вертикально, повернув его вокруг катета ВГ, получим разрез пласта в плоскости падения, где ВD – линия падения, а ВГ – ее проекция на горизонтальную плоскость).

Третий случай является общим: высоты всех точек различны (рис. 2.2-2).

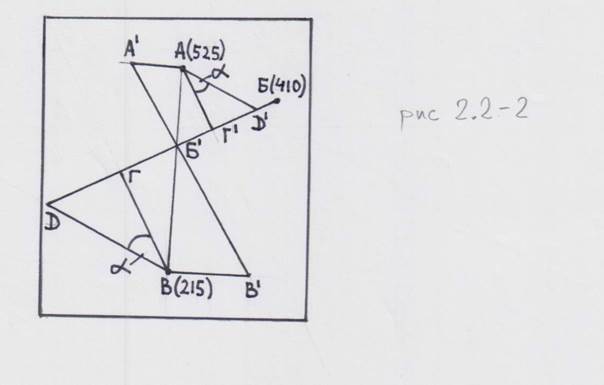
Рис. 2.2-2 Наиболее общий случай определения элементов залегания по трем разновысотным точкам. Масштаб – 1:10000.

A (525 м) >Б (400 м) > В (215 м). Соединим точки крайних (минимального и максимального) значений высот (АВ). Поскольку пласт на изображенной территории непрерывен, на линии АВ есть точка (Б1), в которой пласт будет иметь отметку, равную Б. Чтобы найти эту точку, следует разделить линию АВ пропорционально разнице высот точек, используя масштаб карты. Один из вариантов может выглядеть следующим образом. На перпендикуляре к линии АВ в точке А откладываем разницу высот А-Б в масштабе карты, в точке В – разницу высот Б-В. Соединив полученные точки А1 и В1 прямой, получим на пересечении ее с прямой АВ точку Б1, в которой абсолютная отметка пласта равна таковой в точке Б. Соединив точки Б и Б1, получим линию простирания. Перпендикуляры к ней, опущенные из точек А и В, будут линиями падения (проекцией на горизонтальную плоскость карты). Далее задача решается, как в рассматриваемом втором случае (рис.2.2.-1).

Эта же задача – определение элементов залегания – может решаться и по готовой геологической карте, на которой в силу разных причин могут отсутствовать элементы залегания. На рисунке 2.2-3

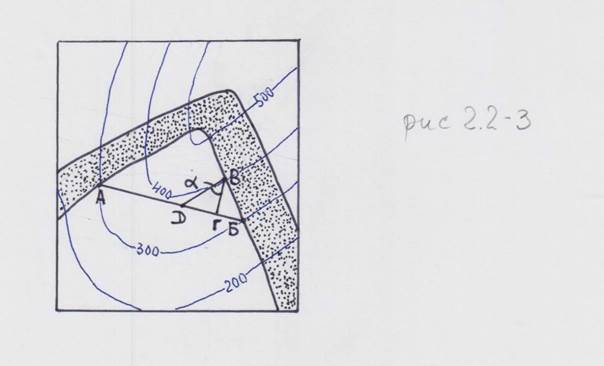
Рис. 2.2-3 Определение элементов залегания пласта по карте. Масштаб – 1:10000.

изображён пласт, откартированный по выходам на местности. Чтобы определить элементы его залегания, необходимо сделать следующее. На одной из поверхностей пласта (кровле или подошве, но обязательно на одной и той же), находим три точки, абсолютная высота которых известна. Пусть это будут точки А и Б (высота 300 м), и В (400 м). Линия АБ в этом случае является линией простирания, а перпендикулярная ей ВГ – линией падения (проекцией на плоскость карты). Если построить отрезок ГД, равный разности высот В – А (Б) в масштабе карты, то угол при точке В – угол падения (решение полностью повторяет таковое, изображенное на рис. 2.2-1).

Задача непрямого определения элементов залегания может стоять не только при анализе имеющейся карты, но и в процессе полевых наблюдений в условиях, когда нет возможности непосредственно компасом измерить азимут и угол падения пласта. В этих случаях, когда невозможно сделать прямые определения в плоскости падения пласта, пользуются совокупностью измерений, сделанных по случайным, произвольным направлениям. Чаще всего это происходит при наблюдениях в стенках шурфа или склонах промоин и оврагов. Достаточным для решения задачи является наличие двух связанных измерений наклона пласта по замеренным направлениям.

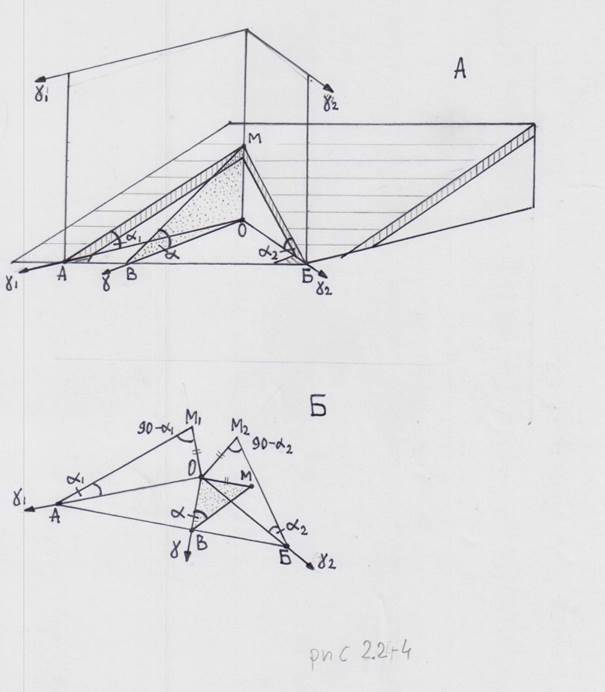
Рис. 2.2-4 Определение азимута и угла падения пласта, для которого по случайным направлениям («гамма 1» и «гамма 2») измерены наклоны («альфа 1» и «альфа 2»).

На рисунке 2.2-4А изображен пласт (заштрихован), вскрытый шурфом, у которого плоскости БМО и АМО – его стенки, перпендикулярные дну (плоскость АОБ). Точками выделен треугольник плоскости падения. В стенках шурфа по направлениям «гамма 1» и «гамма 2» измерены наклоны «альфа 1» и «альфа 2». Необходимо определить истинные азимут («гамма») и угол («альфа») падения. Развернем рисунок, данный в аксонометрической проекции, на плоскость (рисунок 2.2-4Б). В точке О строим направления «гамма 1» и «гамма 2», в той же точке к каждому из направлений восстанавливаем перпендикуляры произвольной, но равной длины (ОМ1 и ОМ2). При точках М1 и М2 строим углы (90 минус «альфа 1») и (90 минус «альфа 2»); тогда при точках пересечения А и Б возникают углы соответственно «альфа 1» и «альфа 2». Соединив А и Б, получаем линию простирания, а перпендикуляр ОБ – линия падения. Тогда «гамма» - ее азимут. В точке О восстанавливаем к ОВ перпендикуляр ОМ (длина отрезка берется равной ОМ1 и ОМ2). Соединив М и В, получим при В угол МВО – истинный угол падения. Если треугольники АОМ1, БОМ2 и ВОМ повернуть вокруг катетов АО, БО и ВО соответственно, то, учитывая равенство отрезков ОМ1, ОМ2 и ОМ, получим объемную картину исходного рисунка 2.2-4А. Эта задача решается также с помощью сетки Бауманна (приложение …).

Задача, обратная приведенной выше, решается, главным образом, при построении геологических разрезов в том случае, когда плоскость разреза не совпадает с плоскостью падения (линия разреза не перпендикулярна линии простирания).

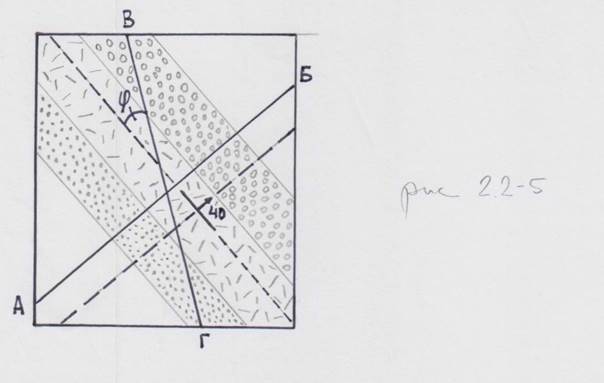
Рис. 2.2-5 Пунктиром обозначены линии падения и простирания.

На рисунке 2.2-5 очевидно, что на разрезе по линии АБ (совпадающем с линией падения) слои имеют наклон, равный углу падения. На разрезе по линии ВГ наклон пластов будет иным, меньшим угла падения. Чтобы его найти, выполним построение, похожее на вышеописанное при рассмотрении прямой задачи (рис. 2.2-4 и пояснительный текст). Здесь известны: азимут («гамма»), и угол падения («альфа») пластов и азимут линии ВГ («гамма 1»), по которой строится разрез, а стало быть, и угол между линией простирания и линией разреза («фи»). Решение выглядит так (рис. 2.2-6).

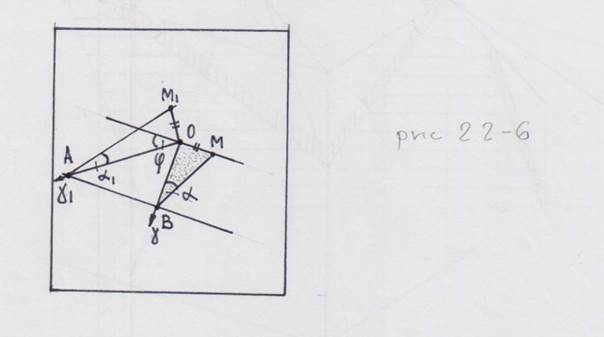
Рис. 2.2-6 Схема графического определения угла наклона в заданном направлении при известных элементах залегания пласта.

В начальной точке О строим линию падения и линию простирания. В произвольной точке В на линии падения строим угол падения («альфа»). При пересечении с линией простирания обозначаем точку М. Через точку В проводим линию простирания. В точке О строим угол между линией простирания и линией разреза («фи»). Продолжив прямую до пересечения с линией простирания, получим точку А. В той же точке О восстанавливаем перпендикуляр к этой прямой (она является линией разреза), откладываем на нем отрезок ОМ1, равный отрезку ОМ; соединяем М1 и А и получаем угол наклона в заданном направлении разреза («альфа 1»). Нетрудно видеть, что полученный чертеж (рис. 2.2-6) аналогичен левой половине рисунка 2.2-4Б. Если повернуть треугольники ВОМ и АОМ1 вокруг катетов ОВ и ОА соответственно, получим объемную картину рисунка 2.2-4А, где треугольник ОАМ1 – стенка шурфа, а перпендикулярный ему треугольник ОАВ – дно. Эта же задача решается с помощью таблицы (приложение …) и номограммы для определения угла наклона в косом сечении.

Рассмотрение пространственной (трехмерной) модели и приведенных способов решения задачи по определению угла наклона в косом сечении убеждает в прямой зависимости наклона от величины угла «фи» (угол между простиранием и заданным направлением разреза) – чем он меньше, тем меньше наклон, вплоть до полного его (наклона) отсутствия в разрезах по простиранию. Наклонно залегающие пласты в разрезах по линии простирания, т.е. в сечениях, перпендикулярных падению, выглядят залегающими горизонтально (угол падения равен нулю).

Построение выхода пласта на поверхность методом стратоизогипс с помощью заложения.

Конфигурация выхода на поверхность любого плоского тела (пласта, дайки) или плоской же поверхности (трещины, сместители разломов) определяется соотношением элементов залегания этих геологических объектов и форм рельефа. Иными словами, выход на поверхность есть след пересечения плоскости (плоских геологических тел) и криволинейной поверхности (рельеф). Возникшая при этом сложная кривая линия и есть геологическая граница на конкретной геологической карте. В условиях недостаточной обнаженности положение этих границ приходится нередко рассчитывать, опираясь на редкие естественные выходы и часто еще более редкие замеры элементов залегания.

Прежде чем приступить к изложению метода расчета и проведения границ на карте, необходимо ввести и определить два понятия: стратоизогипса и заложение.

Стратоизогипса (от stratum – слой, изос – равный, гипсос – высота) есть линия равной высоты, отнесенная к любой поверхности (подошва или кровля пласта, поверхности дайки, трещины, разломы) или, что то же – любая горизонтальная линия на этой поверхности. Очевидно, что это определение совпадает с определением линии простирания. Отличие заключается в том, что для стратоизогипсы точно известна ее абсолютная высота (для линии простирания она не является принципиально важной).

Под заложением понимается расстояние между проекциями соседних стратоизогипс на горизонтальную плоскость, измеряемое в плоскости падения (отрезок проекции линии падения между проекциями соседних стратоизогипс на горизонтальной плоскости). Поясняющая блок-диаграмма изображена на рисунке 2.2-7.

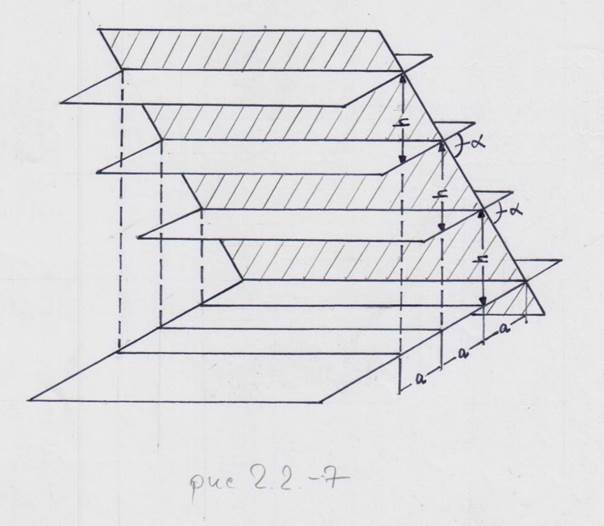
Рис. 2.2-7 Блок-диаграмма, поясняющая взаиморасположение стратоизогипс, их проекций на карту и заложений (a), в зависимости от величины сечения (h) и угла падения (альфа). Заштрихована поверхность пласта.

Очевидно, что величина заложения зависит, с одной стороны, от угла падения, а с другой – определена сечением стратоизогипс (чем больше угол, тем меньше заложение и наоборот).

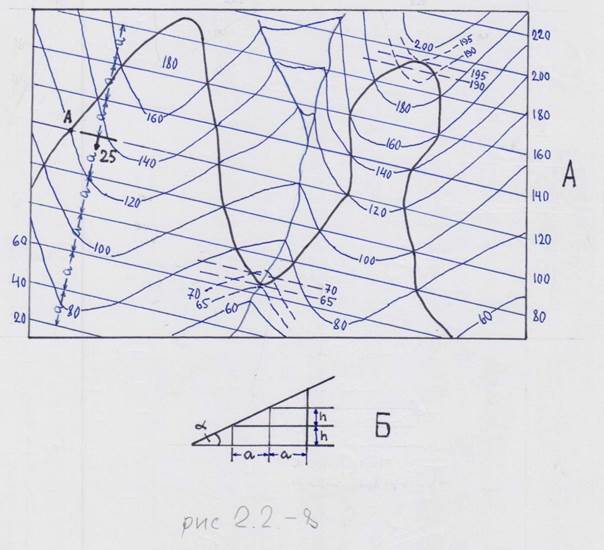
Рис. 2.2-8 Построение выхода пласта по известным элементам залегания методом стратоизогипс с помощью заложения. А – построение выхода; Б – определение заложения. Масштаб – 1:4000, сплошные горизонтали проведены через 20 м (сечение горизонталей). Элементы залегания определены в точке А (Аз пд СВ 12 /_ 25). h – сечение горизонталей; альфа – угол падения; a – заложение.

Метод построения выхода плоскости пласта выглядит так. Допустим, в точке А (рис. 2.2-8А) определены элементы залегания (азимут и угол падения) и абсолютная высота. Строим линии падения и простирания (их проекции на карте). Последняя является стратоизогипсой с известной абсолютной высотой (в данном случае 120 м). Зная масштаб карты и беря сечение стратоизогипс равным сечению горизонталей рельефа, определяем величину заложения с помощью чертежа (рис. 2.2-8Б). Фактически это изображение пласта в разрезе, построенном в плоскости падения. Получив величину заложения, откладываем ее на линии падения-восстания, а через полученные точки проводим стратоизогипсы, номера которых убывают на величину сечения по направлению падения и возрастают в направлении восстания. Очевидно, что пласт будет выходить на поверхность, изображенную на карте с помощью горизонталей рельефа, в тех точках, где пересекаются одноименные стратоизогипсы и горизонтали рельефа. Стратоизогипса по определению – горизонтальная линия на поверхности пласта с известной абсолютной высотой, а горизонталь рельефа – линия на поверхности рельефа, также соединяющая точки с равными абсолютными отметками. Выделив точки, пересечения стратоизогипс и горизонталей одной и той же абсолютной высоты, соединим их плавной кривой, которая и является выходом пласта на поверхность. Для уточнения кривой в местах наиболее резких перегибов рельефа (водоразделы, тальвеги водотоков) можно провести дополнительные горизонтали и стратоизогипсы с меньшим сечением (см. рис. 2.2-8А). Описанный способ в полной мере применим в тех случаях, когда на каком-то участке азимут и угол падения не изменяются (потому-то стратоизогипсы имеют вид прямых линий, а величина заложения неизменна). При переменных значениях азимута падения стратоизогипсы будут изгибаться, а изменение угла падения отразится на величине заложений. Это потребует более сложных построений, но сам принцип останется без изменений.

При изменении угла падения слоя на фоне в целом наклонного залегания возникают своеобразные структурные формы, называемые флексурами. Флексура (flexura – изгиб) – коленчатый изгиб моноклинально залегающих слоев (рис. 2.2-9).

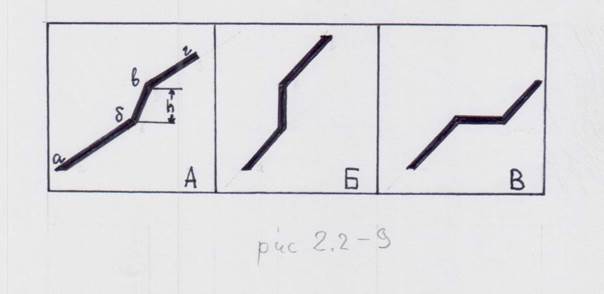Выделяют верхнее, нижнее и смыкающие крылья. Перегибы между ними называются верхним и нижним коленом, расстояние по вертикали между последними – амплитудой (высотой) флексуры. Наиболее распространены флексуры с более крутым, чем и верхнего и нижнего, падением смыкающего крыла. Кроме того, различают вертикальные флексуры (смыкающее крыло практически вертикально) и структурные террасы (смыкающее крыло горизонтально). Своеобразной формой флексуры является так называемый структурный нос – положительная локальная структура на фоне моноклинали, вытянутая по ее падению. В этом случае меняется не только угол, но и азимут падения пласта. Все элементы и виды флексур хорошо обрисовываются стратоизогипсами. Нередко вообще все флексуры, а особенно структурные носы, рассматриваются как складки с одним крылом, а структурные носы именуются антиклиналями (выпуклыми, положительными складками). Амплитуда флексур может достигать сотен и даже тысяч метров, а сами флексуры протягиваются нередко на сотни километров. На геологических картах с помощью стратоизогипс обычно передается структура пластов и тел, не выходящих на земную поверхность (погребенных), т.е. в этом случае показывается глубинная (относительно) структура того участка, который изображен на уровне современного эрозионного среза.

Границы наклонно залегающих геологических тел (пластов), как и сами эти тела, на картах с достаточно выраженным рельефом образуют характерный рисунок в виде изогнутых или ломанных линий, максимальные изгибы (углы) которых приурочены к относительно самым высоким (водоразделы) и самым низким (тальвеги оврагов, ручьев) отметкам рельефа (рис. 2.2-10).

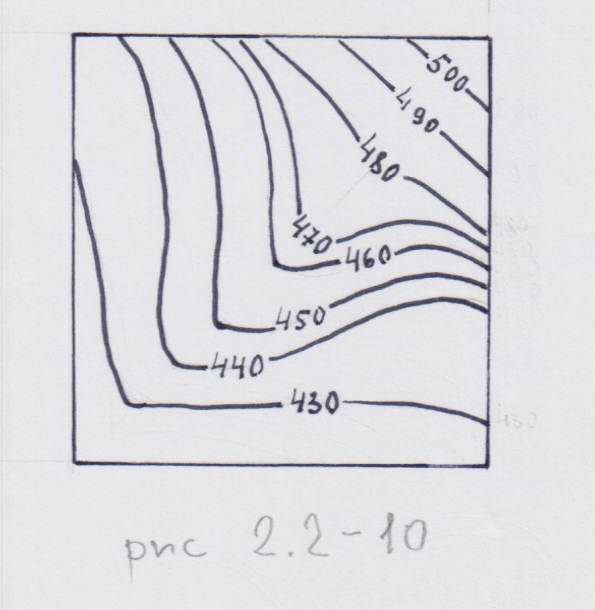
Если мысленно соединить самые высокие или самые низкие точки на одной и той же геологической границе, возникают фигуры, в той или иной степени, напоминающие простые геометрические (треугольники, трапеции, полуэллипсы). Это – так называемые пластовые фигуры. Изломанность линий, а стало быть и форма и выразительность пластовых фигур, определяется рельефом, залеганием тел и их соотношением.

Важнейшей особенностью пластовых фигур является то, что они дают возможность определить направление падения тел (правило пластовых фигур). Возможны два случая. Рассмотрим их на примере наиболее простых (наиболее «геологичных») фигур – пластовых треугольников. Первый случай: вершина угла треугольника, расположенная в самой низкой точке рельефа (тальвег оврага), указывает направление падения пласта. Это возможно, когда пласт и склон падают в разные стороны (рис. 2.2-11),

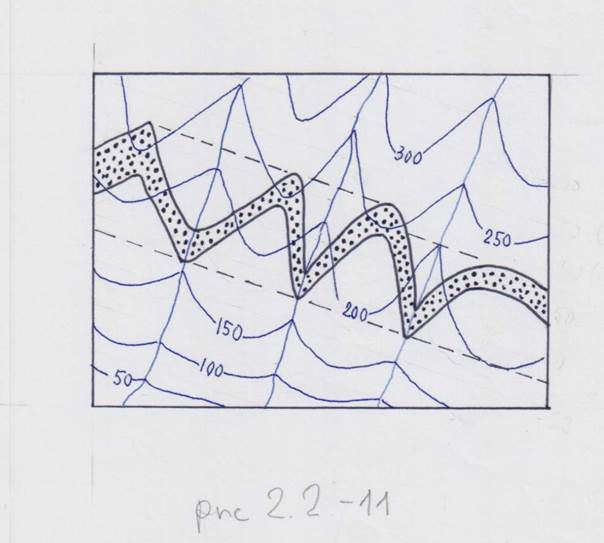
либо когда пласт и склон падают в одну сторону, но пласт – круче (рис. 2.2-12).

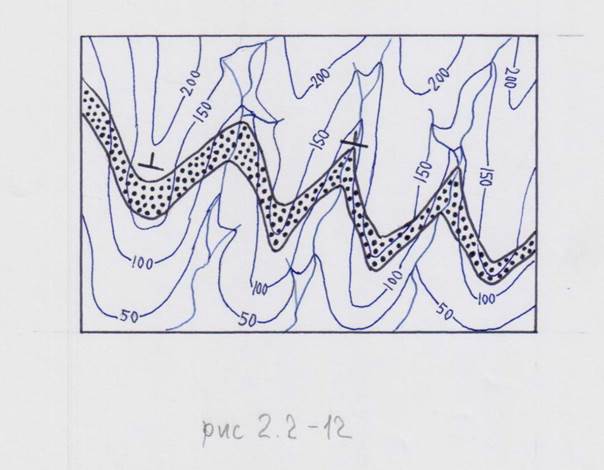Это утверждение легко проверяется с помощью стратоизогипс. Второй случай: вершина угла треугольника, расположенная в самой низкой точке (тальвег), указывает направление восстания пласта (рис. 2.2-13),

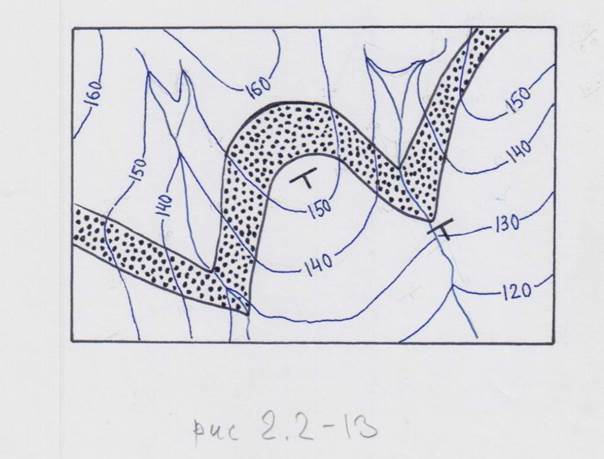
что также легко проверяется с помощью стратоизогипс. Следовательно, на направление падения в этом случае указывает вершина треугольника на водоразделе. Это – тот случай, когда пласт и склон падают в одну сторону, но пласт – положе склона. Во втором случае (пласт и склон падают в одну сторону, но пласт – положе) высота треугольника, образованного пластом, больше, а вершинный угол меньше, чем высота и угол треугольника, образованного горизонталями (изогипсами) рельефа. На карте без горизонталей определение направление падения по пластовым фигурам затруднено, но может быть скорректировано с помощью возраста соответствующих слоев (при нормальном, не опрокинутом, залегании падение – в сторону более молодых пород).

На блок-диаграмме (рис. 2.2-14)

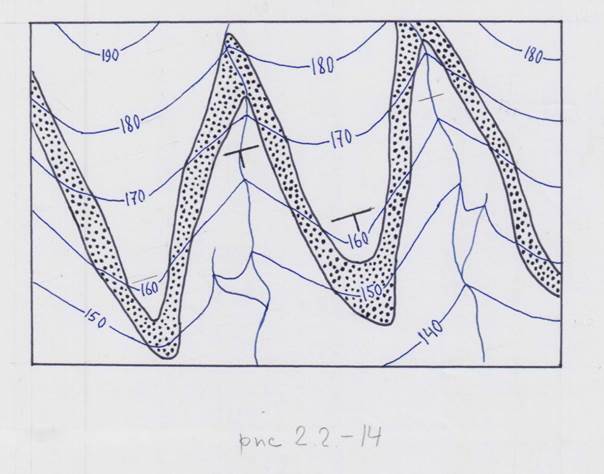показаны принципиально возможные (всего их 5) соотношения залегания пласта (любого плоского геологического тела) и склона: пласт залегает горизонтально (1), вертикально (2), падает в противоположную от падения склона сторону (3), круче (4) и положе (5) склона при падении в одну сторону.

Ширина выхода наклонно залегающих тел на поверхности зависит от мощности, угла падения, формы рельефа и соотношения направлений падения тела и склона. Различные варианты этих соотношений приведены на рис. 2.2-15.

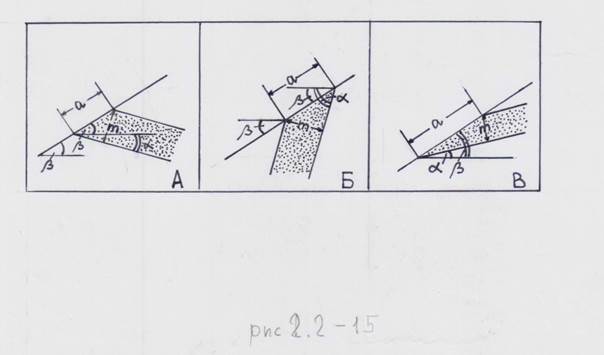
Приведенные схемы используются для графического определения истинной мощности слоя при условии, что все измерения (ширина выхода, угол падения пласта, угол склона) сделаны в плоскости падения пласта. В случае, когда измерения в этой плоскости невозможны, для определения мощности используется так называемая «формула П. М. Леонтовского» (с дополнениями В. С. Милеева):

m = b(sin альфа х cos дельта х sin гамма + cos альфа х sin дельта) (1)

m = b(sin альфа х cos дельта х sin гамма - cos альфа х sin дельта) (2)

m = b(cos альфа х sin дельта – sin альфа х cos дельта х sin гамма) (3)

где альфа – угол падения; b – ширина выхода в сечении, не перпендикулярном линии простирания; дельта – угол склона в этом направлении; гамма – угол между линией простирания и направлением замера.

Вариант (1) применим в случае, когда пласт и склон падают в противоположных направлениях (разница азимутов больше 90 градусов). Варианты (2) и (3) – в том случае, когда пласт и склон падают в одну сторону (разница азимутов меньше 90 градусов), но (2) – при падении пласта круче склона, а (3) – при падении пласта положе склона. Следует сказать, что графическое определение мощности возможно и в этом случае, однако оно достаточно громоздко и практически все же проще использовать математическое решение по формуле.