Правило фаз Гиббса. Условия термодинамического равновесия однофазной и многофазных систем
 В качестве примера применения термодинамических методов исследования получим условия термодинамического равновесия однофазной изолированной системы.
В качестве примера применения термодинамических методов исследования получим условия термодинамического равновесия однофазной изолированной системы.
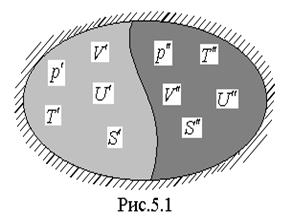
Разобьем мысленно систему на две подсистемы (') и (") (рис.5.1), для каждой из которых известны все термодинамические параметры, причем 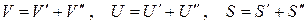 .
.
Для каждой из подсистем, находящихся в состоянии равновесия, запишем уравнения Гиббса:
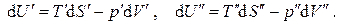
Просуммируем почленно эти два выражения:
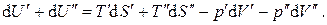
С другой стороны, для изолированной равновесной системы 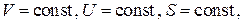 тогда
тогда
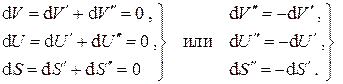
и
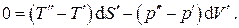
Ввиду произвольности значений дифференциалов 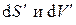 , из последнего выражения находим условия термодинамического равновесия изолированной системы:
, из последнего выражения находим условия термодинамического равновесия изолированной системы:
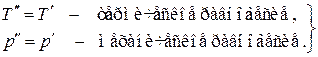
Рассмотрим однокомпонентную систему, состоящую из двух взаимодействующих фаз и заключенную в изолирующую оболочку. Пусть каждая из фаз находится в своем внутреннем равновесии, т.е. характеризуется своим набором интенсивных и экстенсивных параметров. При малом изменении состояния каждой из фаз можно записать для них термодинамические тождества
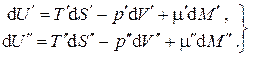 .
.
В силу аддитивности 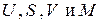 , замкнутости системы и обратимости процесса имеем
, замкнутости системы и обратимости процесса имеем
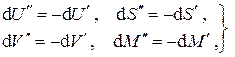
и после почленного суммирования равенств получим
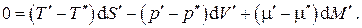
В силу произвольности дифференциалов 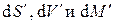 множители в скобках при этих дифференциалах должны быть равны нулю, откуда получаем условия термодинамического равновесия двухфазной однокомпонентной системы:
множители в скобках при этих дифференциалах должны быть равны нулю, откуда получаем условия термодинамического равновесия двухфазной однокомпонентной системы:
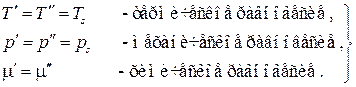
Химический потенциал по определению сам является функцией "естественной" пары переменных 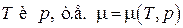 , таким образом, условие равновесия фаз может быть записано в виде
, таким образом, условие равновесия фаз может быть записано в виде
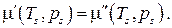
Вид функций 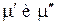 от T и p в общем случае различен для каждой из фаз, поэтому последнее условие не является тождеством. Это есть алгебраическое уравнение, связывающее температуру и давление в равновесной двухфазной системе. Таким образом, в двухфазной однокомпонентной системе температура и давление однозначно связаны. Объем же системы может принимать произвольное значение в зависимости от соотношения между массами фаз.
от T и p в общем случае различен для каждой из фаз, поэтому последнее условие не является тождеством. Это есть алгебраическое уравнение, связывающее температуру и давление в равновесной двухфазной системе. Таким образом, в двухфазной однокомпонентной системе температура и давление однозначно связаны. Объем же системы может принимать произвольное значение в зависимости от соотношения между массами фаз.
Состояние равновесия двухфазной системы называется состоянием насыщения, а равные для фаз температура и давление – параметрами насыщения. 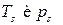 (saturation ≡ насыщение).
(saturation ≡ насыщение).
5.4.4. Уравнение Клапейрона – Клаузиса
В дальнейшем будем рассматривать только фазовые переходы I рода, во время которых происходит изменение агрегатного состояния, а точнее, переход "жидкость–пар", который весьма часто имеет место в тепловых машинах.
Формула Клапейрона–Клаузиуса связывает температуру насыщения (температуру кипения) Ts с давлением насыщения ps. Для нахождения этой зависимости запишем в дифференциальной форме условие равновесия фаз:
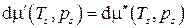
или
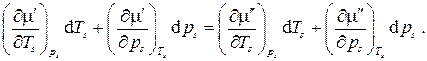
Так как химический потенциал совпадает с удельной свободной энергией Гиббса 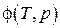 , то
, то
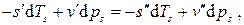
откуда
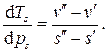
Учтя определение удельной теплоты парообразования, получаем зависимость, известную как формула Клапейрона - Клаузиуса
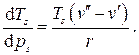
Так как 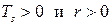 , а удельный объем в парообразном состоянии больше, чем в жидком, температура кипения увеличивается с увеличением давления.
, а удельный объем в парообразном состоянии больше, чем в жидком, температура кипения увеличивается с увеличением давления.
Лекция 11
Дата добавления: 2021-07-22; просмотров: 482;











