ИССЛЕДОВАНИЕ И ОПТИМИЗАЦИЯ МЕТАЛЛУРГИЧЕСКИХ ПРОЦЕССОВ НА ОСНОВЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Как было показано при рассмотрении предыдущего вопроса, исследование и управление это лишь на первый взгляд различные, а в (действительности две неразрывные стороны одной и той же проблемы целенаправленного воздействия на объект, ори­ентированного на получение определенных заранее задан­ных результатов. Вопрос состоит лишь в том, что в зависи­мости от конкретных условий на первый план может вы­двигаться одна из этих сторон.

Если объект хорошо изучен, ясен алгоритм управления им, то преобладающими стано­вятся конкретные задачи управления, например, получение (определенных технологических или технико-экономических показателей: химического состава, прочностных свойств металлургической продукции и т. д.

В ряде же других случаев, когда уровень знаний о про­цессе недостаточен, неясны способы воздействия на него (т. е. алгоритмы управления), на первый план выдвигаются вопросы исследования объекта с целью более полного вскрытия его внутреннего механизма и разработки на этой основе рациональных способов управления.

Эти задачи решаются с помощью наиболее полных моделей исследо­вательского плана. В про­цессе таких исследований могут быть получены далеко идущие результаты, направленные, например, на коренное из­менение технологии производства или конструкции агрегатов или даже на создание новых процессов и агрегатов. По существу это тоже своеобразное управление, но толь­ко более широкого плана. Общим же у этих двух сторон Проблемы является стремление вести исследование и управ­ление оптимальным способом.

Управление даже сравнительно простыми объектами невозможно без их исследования, а рациональная организация исследования требует его постановки как задачи управления и последнее наиболее эффективно реализуется на основе подстраиваемой модели, что позволяет получать характеристики объекта компенсационным методом, сводя до минимума вмешательство в нормальное функционирование объекта и перенося большую часть экспериментов объекта на модель. В этом случае задача исследования логично ставится как задача оптимального управления, выражающаяся либо в получении модели заданной точности с минимальными затратами, либо в минимизации ошибки.

Постановка задачи и методы оптимизации

Постановку задачи оптимального управления проиллюстрируем схемой, представленной на рис. 7, которая является с одной стороны упрощением, с другой стороны обобще­нием схемы на рис. 6

Устройство управления УУ состоит здесь из модели объ­екта, воплощающей в себе формализованные на момент синтеза алгоритма априорные знания об объекте, и алго­ритма управления или оптимизации А, для выбора которо­го используется более широкая, возможно даже концеп­туальная (мысленная) модель. Она же используется в оп­ределенной мере и при формировании цели Q, которая за­дается в основном вышестоящим звеном системы управ­ления.

Ситуация, которая складывается в каждый момент в процессе управления характеризуется состоянием среды X состоянием объекта Y и целью управления. Путем выбор управляющих воздействий U можно изменять состояние объекта Y, модель которого имеется в нашем распоряжении.

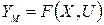(13)

Строго говоря, состояние объекта определяется соот­ношением

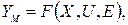(14)

где E —вектор неконтролируемых возмущений, обуслов­ленный неизмеряемыми входами, постепенным изменением характеристик объекта во времени, а в некоторых случаях также неточностью задания структуры модели.

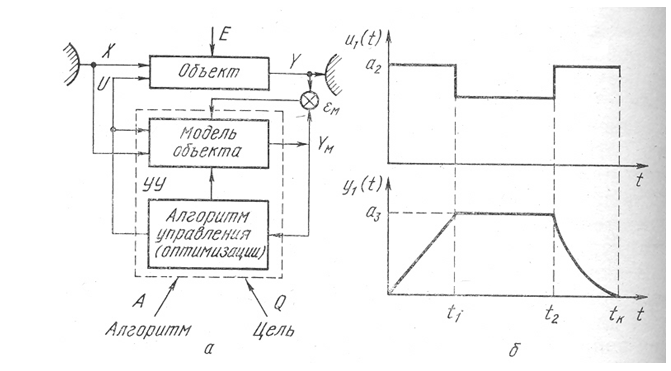
Для простоты дальнейших рассуждений при постанов­ке задачи будем считать, что Y= Y_М, а ошибка модели ε_М, зависящая в первую очередь от Е достаточно эффективно устраняется блоком адаптации модели или идентификато­ром (см. рис. 6).

Достижение цели управления Q* сводится к выполне­нию следующих целевых соотношений:

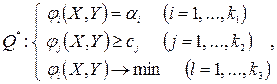(15)

Функци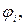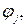и и 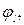, а также числа а_i и с_j, должны быть за­даны на стадии формулировки целей управления и ограни­чений. Для дальнейшего анализа удобно записать эти соот­ношения в канонической векторной форме:

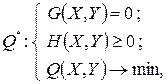(16)

где G — функция ограничений типа равенств;

H — функция ограничений типа неравенств;

Q — функция качества.

Реализация условий (16) возможна путем соответству­ющего изменения состояния Y объекта за счет выбора оп­ределенного управления U, что приводит к следующей экстремальной задаче:

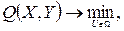(17)

где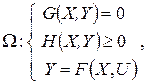

решение которой U* и является оптимальным управлением.

Ресурс, выделяемый на управление, выражается системой равенств и неравенств в области Ω. Для прогнозирования состояния объекта Y необходима его модель F [см. формулу (13)]. Следует заметить, что хотя задача в целом является экстремальной, однако первоочередным является выполнение ограничений Ω, а экстремальные цели Q достигаются лишь при условии выполнения неэкстремальных целей т. е. ограничений.

Например, при оптимизации управления каким-либо сталеплавильным процессом в первую очередь естественно, выполняются требования попадания в заданные ГОСТом пределы по химическому составу и температуре, ограничения на сырьевые ресурсы и лишь при выпол­нении этих условий решается задача минимизации затрат или себестоимости продукции.

Рассмотренную выше задачу (17) целесообразно представить в следующем виде:

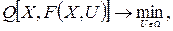(18)

где

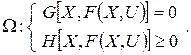
В зависимости от вида модели F, т. е. от того, является ли F функцией или оператором, получают различные за­дачи, которые решаются различными методами.

Задача синтеза управления статическим объектом, для которого модель F является функцией, заключается в ми­нимизации векторной функции Q (X, U) путем изменения q управлений u₁..., u_q, удовлетворяющих ограничениям Ω, наложенным на U. Состояние среды X (значения измеряе­мых, но неуправляемых входов) при этом должно быть из­вестным.

Примером такой задачи может служить планирование производства. Здесь U — производственный план; X — по­ставка сырья; G — требования к номенклатуре продукции, соблюдению норм безопасности и т. д.; Н — требования к качеству продукции, производственные нормативы и огра­ничения. В качестве экстремальных целей могут служить производительность труда, себестоимость продукции и т. д. Это наиболее характерный пример задачи математи­ческого программирования, отличающейся тем, что исходное управление представляет собой набор пара­метров u₁..., u_q, a Q, G и H являются векторными функциями управления U. Если функции Q, G и Н линейны, то имеет место широко распространенная и теоретически хорошо разработанная задача линейного программирования, при­меняющаяся прежде всего для решения вопросов планиро­вания и управления производством в условиях ограничен­ных ресурсов.

Рассмотрим теперь динамический объект, для которого F — оператор. Тогда управление U представляет собой векторную функцию времени U(t), a Q, G и Н являются функционалами. При этом задача (18) становится ва­риационной.

Пример. Необходимо получить заданное содержание углерода в конвертере за минималь­ное время. При этом максимально упростим постановку задачи. Допустим, что изменение содержания углерода в кон­вертерной ванне, начиная с момента заливки чугуна, опи­сывается дифференциальным уравнением следующего вида:

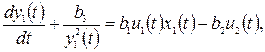(19)

где y₁(t) — содержание углерода в ванне; u₁(t) и u₂(t) — управляющее воздействие соответственно интенсивностью продувки и положением фурмы; x₁(t) — воздействие среды, например степень чистоты продувочного кислорода или его давление.

Для решения поставленной задачи необходимо миними­зировать функционал Q (t) = Q[u₁(t), u₂(t), x₁(t)] в усло­виях наложения целого ряда ограничений на управления.

Более конкретно задача представляется в следующем виде:

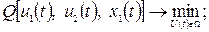(20)

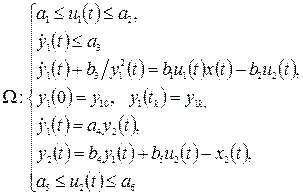(21)

Здесь выражение (20) — целевая функция, подлежа­щая минимизации, а выражение (21) — система ограниче­ний.

Первое соотношение этой системы накладывает ограничения на интенсивность продувки кислородом,

второе – на скорость обезуглероживания в связи с пропускной способностью газоотводящего тракта.

Третье уравнение представляет собой модель обезуглероживания,

четвертое – граничные условия (содержание углерода в начале и конце продувки).

Соотношение пятое накладывает ограничение на скорость обезуглероживания в связи со скоростью нагрева,

шестое представляет собой модель нагрева, где скорость нагрева y₂(t) описывается как зависимость от скорости обезуглероживания 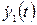, положения фурмы u₂(t) и по­терь тепла в окружающую среду х₂(t).

Седьмое соотноше­ние накладывает ограничение на положение фурмы в связи с возможностью переокисления шлака и выбросов из кон­вертера при слишком высоком положении фурмы а₆ и опас­ностью преждевременного выхода ее из строя при слишком низком положении a₅.

Естественно, в связи со сложностью процесса не учтен еще целый ряд ограничений, но для понимания задачи до­статочно и такой ее постановки. Количественное решение этой задачи представляет значительные трудности как ме­тодического, так и вычислительного характера, поэтому ограничимся лишь упрощенным качественным ее анализом.

На рис. 7, б показан график изменения интенсивности продувки по ходу конвертерной плавки и траектория изме­нения скорости обезуглероживания. Здесь можно видеть, что на первом участке 0 —t₁ поддерживается максималь­ная интенсивность продувки, допускаемая ограничением а₂. В этот период наряду с углеродом окисляются также кремний и марганец. Распределение затрат кислорода на окисление этих элементов учитывается в уравнении (19) коэффициентом b₁ и являющимся функцией их концентра­ций. Причем содержание двух последних элементов, имею­щих большее сродство к кислороду, чем углерод, к концу первого периода доходит практически до следов. В связи с этим практически весь вдуваемый кислород начинает расходоваться на реакцию обезуглероживания, протекающую с большим выделением СО. При этом начинает дейст­вовать ограничение а₃, связанное с пропускной способ­ностью газоотводящего тракта. Поэтому на втором участке t₁ — t₂ скорость обезуглероживания за счет выбора соот­ветствующего значения u₁(t) поддерживается на макси­мально возможном уровне с учетом ограничения а_з. С мо­мента t₂ наряду с окислением углерода начинает заметно сказываться накопление кислорода в металле и шлаке, что приводит к повышению содержания оксидов железа в шлаке.

В уравнении (19) это отражается через возрастание второго члена в левой части. Значительную роль в этот период начинает играть ограничение по синхронизации процессов обезуглероживания и нагрева, которое в свою очередь связано с ограничением на оскисленность шлака.

Варьируя управляющими воздействиями u₁(t) и u₂(t), можно свести к минимуму продолжительность продувки, т. е. функционал Q (t).

Таким образом, оптимальное управление динамическим объектом требует решения вариационной задачи, в которой искомые уравнения представляют собой функции времени, a Q, G и H являются заданными функционалами управления U (t), Аналитически задача эта решается до­вольно сложно, чаще всего ее стараются свести к задаче математического программирования.

Имеются хорошо разработанные теоретически методы решения этой задачи, однако при их практической реализации чаще всего возникают определенные трудности. Наиболее известными из этих методов являются принцип мак­симума Понтрягина и динамическое программирование.

Принцип максимума применяется для динами­ческих объектов, модель которых может быть представлена в виде системы обыкновенных дифференциальных урав­нений

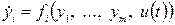(22)

с заданными начальными условиями при t = 0, 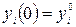и скалярным управлением. В векторной форме эта система записывается следующим образом:

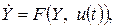
где Y(t) – вектор состояний объекта;

F — вектор заданных функций, определяющих мо­дель объекта.

Задача ставится следующим образом: необходимо пе­ревести объект из состояния Y₀ в заданное состояние Y*, Причем траектория Y(t) и управление u(t) должны удов­летворять заданным ограничениям и экстремальной цели — минимуму заданного функционала

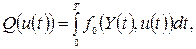(23)

где f₀ (Y(t), u(t)) – заданная функция.

В качестве такого функционала выбирают обычно траты на управление. При f₀(·) = 1 получаем Q = T, т.е. время перехода из состояния Y₀ в Y*. Принцип максимума позволяет свести эту задачу к задаче максимизации так называемой функции Гамильтона, приводящей из состояния Y₀ в какое-то промежуточное (текущее) состояние Y(Т). Это так называемый цикл быстрой оптимизации. Затем решается задача попадания в заданную точку Y* Путем выбора соответствующих начальных условий С(с₁ с_m), для чего минимизируется следующая невязка

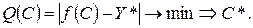(24)

Эту задачу решают поисковыми методами (цикл медленной оптимизации), которые требуют больших затрат машинно­го времени, причем очень резко возрастающих в зависи­мости от размерности объекта т, что ограничивает применимость этого метода.

Метод динамического программирова­ния применяется обычно для многоэкстремальных вариа­ционных задач, требующих в принципе для своего решения организации полного перебора. Он позволяет ввести опре­деленную целенаправленность и таким образом значительно сократить полный перебор всех допустимых вариантов уп­равления. В основе этого метода лежит предположение о выполнимости так называемого «принципа оптимальности», заключающегося в том, что оптимальное поведение объек­та и дальнейшее управление зависит только от его исход­ного состояния и не зависит от предыстории попадания в это состояние. Для применимости рассматриваемого метода необходимо иметь модель объекта управления, позволяю­щую достаточно удовлетворительно предсказывать буду­щее поведение объекта при определенном управлении.

Общая постановка задачи и вид функционала качества аналогичны предыдущему методу. Идея решения задачи представляется следующим образом. Прежде всего задача дискретизируется, что позволяет рассматривать управле­ние для каждого определенного интервала времени:

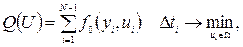(25)

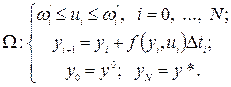
Далее для простоты остановимся на случае равноотстоя­щих единичных интервалов времени, т. е. Δt = l. Решение ищется, начиная с конца процесса (t = T), поскольку, ис­ходя из принципа оптимальности, оптимальное решение, полученное на каком-то отрезке [t₁, T], будет «куском» ре­шения исходной задачи на отрезке. [0, Т]. На последнем (N—1)-м шаге решается задача попадания в конечную точку состояния y_N = y*, т. е. определяется корень уравне­ния

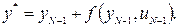
На этом шаге не до оптимизации, так как нужно удовлет­ворить граничному условию у_N = у* любой ценой, которая зависит от y_N-1 и равна

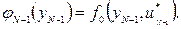
где f₀ — функция затрат.

Далее, двигаясь от конца (t=T) к началу (t = 0), рас­сматривается следующий (N — 2)-й шаг (предпоследний), который, как и все предыдущие, делается из пока неизвест­ного состояния y_N-1. Приращение минимизируемого крите­рия на этом шаге равно f₀(y_n-2, u_n-2).

В соответствии с принципом оптимальности необходимо минимизировать сумму затрат на этом и последующем шаге, т. е.

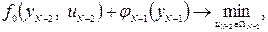
где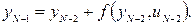

Из этих соотношений находится зависимость оптималь­ных управлений 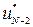для данного шага от неизвестных значений y_N-2 и минимальное значение затрат на двух последних (в общем случае на всех последних) шагах

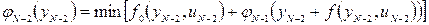
Таким образом, двигаясь с конца к началу, предвари­тельно определяют следующие необходимые для дальней­ших расчетов функции

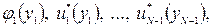(26)

Которые характеризуют минимальные затраты при движе­нии из исходного состояния у⁰ в конечное у* и зависимость оптимального управления каждого шага от его начальных условий.

Далее синтез оптимального управления идет с начального до конечного состояния. Оптимальное управление на первом шаге определяется из условия 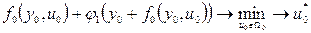, а точка оптимальной траектории на первом шаге .

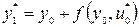Затем, используя полученные выше функции (26) имеем

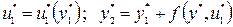и т.д. до .

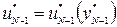В результате определяется оптимальное управление 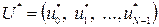и соответствующая ему оптималь­ная траектория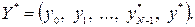

Метод динамического программирования позволяет до­статочно просто учитывать не только ограничения на уп­равления, но и ограничения, накладываемые на оптималь­ную траекторию, дает возможность находить глобальный минимум при решении многоэкстремальных задач. Однако применимость этого метода ограничивается задачами уп­равления объектами размерности не более 2—3 (по коли­честву управляющих воздействий), так как объем необхо­димой памяти за счет многомерности таблиц функций (26) увеличивается почти на порядок для каждой единицы раз­мерности. В связи с этим теоретические представления обычно используются для правильной постановки задач оптимизации, решение же их чаще всего осуществляется поисковыми методами.

Интересные возможности для реализации как аналити­ческих, так и поисковых методов оптимизации открывают­ся при использовании гибридных ЭВМ, сочетающих пре­имущества аналоговых и цифровых ЭВМ. Особенно пер­спективным это становится для современных ЭВМ.

Рассмотрим принцип решения динамической задачи не­линейного программирования, относящейся к классу слож­нейших оптимизационных задач, требующих длительных расчетов даже на быстродействующих ЭВМ. Постановка этой задачи имеет следующий вид:

………………………….

………………………….

…………………………..

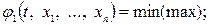
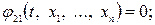
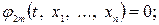
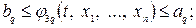
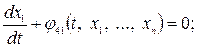
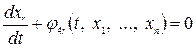
с заданными начальными условиями

,

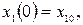
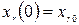где x₁, ..., х_n — варьируемые переменные, например управ­ления;

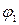— заданная функция многих переменных (функция качества), для которой необходи­мо найти минимум или максимум;

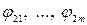— заданные нелинейные функции, образующие систему конечных уравнений;

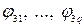— заданные функции, образующие систему не­равенств;

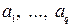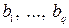, — границы неравенств;

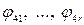— заданные функции, входящие в систему обыкновенных дифференциальных уравне­ний;

n — число варьируемых переменных;

m — число конечных уравнений;

q—число неравенств;

r — порядок системы обыкновенных дифферен­циальных уравнений.

Решение поставленной задачи основано на методе ко­ординатного поиска, алгоритм которого состоит из следу­ющих операций: определение минимума функции в заданном направлении, выработка команды перехода на новое направление, формирование направления поиска, форми­рование траектории поиска. Операции алгоритма выполня­ются в следующей последовательности. Вырабатывается команда формирования первого направления поиска и фор­мируется движение в этом направлении. Координаты движущейся точки используются для вычисления штрафной функции как функции времени. При движении по заданному направлению минимизируемая функция изменяется во времени. Убыванию этой функции соответствует отрица­тельная производная, возрастанию — положительная производная по времени, а экстремуму функции — ее нулевое значение. В момент обращения производной в нуль выраба­тывается команда перехода на новое направление поиска. Таким образом, в этой части алгоритма используется классический принцип определения экстремумов, что оказывается возможным благодаря чрезвычайно большому быстродействию аналоговой части, позволяющей параллельно решать все уравнения и неравенства, приведенные в постановке задачи. Цифровая часть используется главным образом для формирования логики изменения направлений поиска.

Траектория движения в минимум штрафной функции, в которую входят минимизируемые функции, является лома­ной линией с прямолинейными участками. Поиск решения представляется в виде развернутого во времени процесса на экране электронно-лучевого индикатора, что делает весьма наглядным и физичным постановку и решение за­дачи. Затраты машинного времени на гибридной ЭВМ. не­соизмеримо малы по сравнению с цифровой ЭВМ.

Остановимся в заключение этого подраздела на поиско­вых методах, входящих в той или иной форме в большин­ство алгоритмов оптимизации (минимизации ошибки модели; методы Гаусса — Зайделя (поочередное варьирование переменных); метод крутого восхождения).

Широкое распространение получил так называемый симплексный метод поиска, который хотя и не позволяет получить математического описания иссле­дуемой поверхности, но требует для своей реализации еще меньшего числа опытов, чем предыдущий, и сравнительно легко поддается алгоритмизации для ЭЦВМ. Еще одним достоинством этого метода является его приспособляемость к свойствам поверхности (метод деформируемого много­гранника).

Рассмотрим основную идею симплексного метода опти­мизации. Симплексом называется регулярный многогран­ник, имеющий n+1 вершину при n переменных. Например, для случая двух переменных регулярный симплекс пред­ставляет собой равносторонний треугольник, для трех пе­ременных— тетраэдр и т. д.

При поиске минимума целевой функции пробные опы­ты (векторы) выбираются в точках, находящихся в верши­нах симплекса (точки 1—3 на рис. 8).

x2

Рис. 8. Оптимизация с использованием метода

Далее из вершины, где целевая функция максимальна (точка 3) проводится проектирующая прямая через центр тяжести симплекса, точка 3 исключается и строится новый симплекс, называе­мый отраженным, из оставшихся прежних точек 1, 2 и од­ной новой точки 4, расположенной на проектирующей прямой. Аналогичным способом строится следующий симплекс и так до тех пор, пока он не начнет вращаться вокруг об­ласти экстремума, где размеры симплекса приходится уменьшать.

Некоторые трудности, возникающие при использовании регулярных симплексов, особенно отсутствие ускорения поиска и сложности его проведения на искривленных «ов­рагах» и «хребтах», привели к необходимости совершенст­вования этих процедур. Так, например, Нелдером и Мидом предложен метод, в котором симплекс может изменять свою форму (деформироваться) и таким образом по существу уже не будет оставаться симплексом. Этот так называе­мый метод деформируемого многогранника.

Начальный многогранник здесь выбирается обычно в виде регулярного симплекса (хотя это не обязательно). Процедура отыскания вершины, в которой целевая функ­ция имеет лучшее значение, состоит из следующих опера­ций: отражения (как и в предыдущем методе), растяжения, сжатия, редукции (уменьшение всех граней в 2 раза), c помощью трех последних операций деформируемый многогранник адаптируется к топологии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума. Имеются прикладные программы для реализации этого метода на ЭВМ.

Исследование модели, а точнее исследование объекта с помощью модели, является одним из важнейших этапов процесса математического моделирования. Машинные эксперименты на математических моделях, в противополож­ность экспериментам на реальных объектах, позволяют на­ряду с сокращением дорогостоящих и трудноорганизуемых промышленных опытов, сопровождающихся обычно нару­шениями технологии и потерями производства, получить в ряде случаев интересные результаты, не достижимые при промышленных экспериментах, поскольку на моделях мо­гут быть воспроизведены предельные, критические и дру­гие особые режимы, реализация которых в производствен­ных условиях представляет большие трудности. Кроме того возможности перебора вариантов и пробных воздействий на моделях практически не ограничены.

Любое исследование в принципе должно быть целена­правленным, поэтому при его организации необходимо поль­зоваться постановкой задачи оптимального управления и методами оптимизации. Организация управляемого исследо­вательского процесса может представляться либо как зада­ча полной автоматизации эксперимента путем реализации рассмотренных выше алгоритмов, либо как задача диалогового взаимодействия исследователя и ЭВМ.

Основная литература

1. Цымбал В.П. Математическое моделирование металлургических процессов: Учебное пособие для вузов. М.: Металлургия, 1986. 240 с.

2. Царегородцев А.В. Математическое моделирование управляющих систем: Учеб. пособие.— М.: Изд-во РУДН, 2003. — 80 с.