РОЛЬ МОДЕЛЕЙ ПРИ СИНТЕЗЕ АЛГОРИТМОВ УПРАВЛЕНИЯ
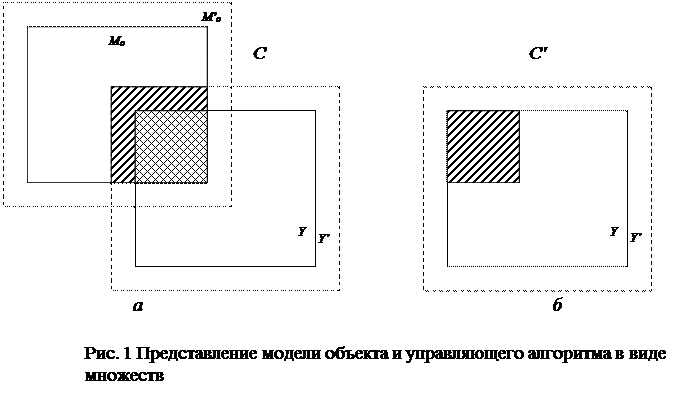
Учет отмеченной выше классификации целесообразен также при оценке роли моделей в синтезе алгоритмов управления и выборе рациональных управляющих воздействий. Попытаемся сначала рассмотреть эту проблему с позиций теории множеств. Удобно объект управления, заместителем которого в наших рассуждениях будет служить модель объекта Мо, отражающая существующие знания о нем, управляющее устройство Y и систему управления в целом С рассматривать в виде пересечения двух множеств (рис. 1, а)
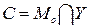 . (1)
. (1)
Очевидно, охваченной управлением следует считать ту часть объекта, элементы которой принадлежат одновременно также управляющему устройству. Следует отметить, что большинство металлургических объектов являются управляемыми существенно неполно. Совершенствование систем управления возможно как за счет получения новых знаний об объекте — расширение множества Мо до М'о (рис. 1. а), так и за счет совершенствования управляющих устройств (алгоритмов) — расширение множества Y до Y'.
Однако и в этом случае задача сводится к увеличению числа элементов объекта, охваченных управлением, то есть к повешению количества информации об объекте. Резервы совершенствования систем управления в связи с отмеченным выше весьма велики. Следует подчеркнуть большую роль в этом процессе моделей объекта более широких (рис. 1, а), чем это необходимо, исходя из требований и критериев существующей системы управления (рис. 1, б). В последнее время ценность так называемых «накопленных» или «познавательных» моделей начинает осознаваться все более четко.
Модель же, построенная исходя из требований конкретного критерия управления и полностью подчиненная задачам определенной системы управления теряет свои эвристические свойства и может использоваться лишь для параметрической настройки системы, входя по существу в управляющий алгоритм (рис. 1, б). При этом мы имеем дело с вырожденным случаем, сводящимся к универсальному множеству, что подтверждается приводимыми ниже рассуждениями.
Обозначим усеченную модель, полученную в соответствии с требованиями конкретного критерия и алгоритма управления через Mо1. Если
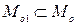 ; (2)
; (2)
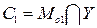 ; (3)
; (3)
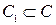 ; (4)
; (4)
I=C1=Y (5)
где I — универсальное множество, т. е. такое множество, в котором полностью содержится любое другое множество, то
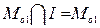 (6)
(6)
т. е. общая часть множества I и множества Mо1 с самим множеством Mо1.
Таким образом, свойства всей системы определяются выбранной моделью.
Свойства управляющего устройства Y в этом случае качественно не изменяют свойств системы, не расширяют множества С1 если остаются в силе условия (4), (5). Использование модели полностью подчиненной требованиям каким-либо образом выбранного критерия управления целесообразно лишь для случая определенной фиксированной структуры системы и выбранного алгоритма управления при параметрической настройке системы управления, когда задача дальнейшего развития системы не ставится, поскольку такая модель новой информации о направлениях структурного совершенствования системы дать не может.
Если объединение множеств Мо и Y рассматривать как совокупность знаний об объекте и управляющем устройстве 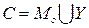 , то для случая (рис. 1, б) имеем
, то для случая (рис. 1, б) имеем
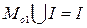 (7)
(7)
где I=C1=Y. Таким образом объединение состоит из тех же элементов, что и I=C1 т. е. свойства системы знаний от свойств МО1 не зависят. Такая модель не открывает путей совершенствования системы С1, так как она сама получена исходя из требований алгоритма управления Y и по существу является входящей в него.
Таким образом, показана целесообразность тесной увязки задач исследования и управления, использования для этого моделей разных уровней сложности. При этом для синтеза алгоритма управления, определения эффективных управляющих воздействий и совершенствования системы управления необходима модель объекта более широкая, чем модель — для функционирования этой системы. Модель же, полученная исходя из требований конкретного критерия управления, может использоваться только для параметрической настройки алгоритма управления, являясь его основой. Для определения путей дальнейшего совершенствования системы такая модель непригодна.
Остановимся теперь на более простом и конкретном случае — задаче аналитического конструирования закона (алгоритма) регулирования. Рассмотрим структурную схему (рис. 2) одноконтурной системы автоматического регулирования с отрицательной обратной связью.
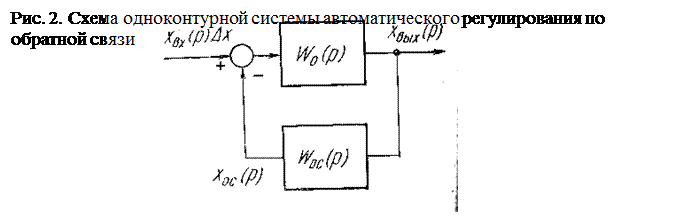
Здесь Wo(p) и Woc(p) — передаточные функции (модели) прямого канала (объекта управления) и канала обратной связи (регулятора).
Для простоты будем считать, что чувствительный элемент и регулирующий орган включены в состав объекта, а исполнительный механизм — в состав регулятора.
Связи между входами и выходами для звеньев прямого и обратного каналов описываются следующими уравнениями:
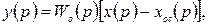
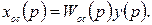
Исключив отсюда хос(р), получим
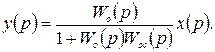 (8)
(8)
Учитывая, что передаточная функция рассматриваемой замкнутой системы Wc (p) = у(р)/х(р), имеем
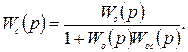 (9)
(9)
Из этого выражения видно, что если известна передаточная функция (модель) объекта Wо(p) то, задавшись требуемыми свойствами системы Wc(p), можно в явном виде найти закон регулирования
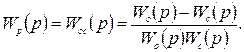 (10)
(10)
Таким образом, при известной модели объекта задача аналитического синтеза регулятора решается весьма просто, естественно, если получаемая передаточная функция физически реализуема. Задача существенно осложняется, если математическое описание характеристик объекта отсутствует. Закон регулирования в этом случае может быть определен лишь весьма приближенно с использованием поисковых методов и лишь для сравнительно простых объектов, чаще всего одноконтурных. Для сложных же многосвязных объектов есть опасность навязывания им алгоритмов управления не согласованных с их внутренними свойствами (физическим механизмом), что может привести к нерациональным затратам управляющих воздействий или даже к ухудшению функционирования объекта.
Теоретически синтезировать передаточную функцию системы с обратной связью, не зная передаточной функции прямого канала, можно лишь в следующем предельном случае. Представим передаточную функцию прямого канала в виде произведения
W0(p) =k1W1 (р)
где k1 — коэффициент передачи этого звена;
Тогда формула оператора замкнутой системы (9) перепишется следующим образом
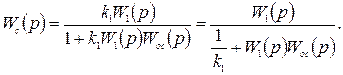
Устремив коэффициент передачи k1 в бесконечность, получаем соотношение
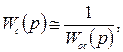 (11)
(11)
которое носит название предельного свойства обратной связи и позволяет сделать вывод, что при достаточно большом усилении в прямом канале свойства системы с отрицательной обратной связью практически полностью определяются лишь свойствами обратной связи и не зависят от характеристик прямого канала, естественно, если система при этом остается устойчивой. Системы, синтезируемые с использованием указанного свойства, называют системами с нулевой ошибкой или нулевой чувствительностью.
К числу реально осуществимых систем такого рода относятся высокоточные измерительные системы компенсационного типа(автоматические потенциометры и мосты) и решающие блоки аналоговых вычислительных машин, в основу синтеза которых положено предельное свойство отрицательной обратной связи (11). Так коэффициент усиления современных усилителей 'постоянного тока третьего поколения, на которых строятся решающие элементы, достигает 108, т. е. соотношение (11) выполняется с весьма высокой степенью приближения.
Таким образом, чтобы получить решающий блок, реализующий заданную функцию Wc(p), необходимо включить в обратную связь операционного усилителя элемент, реализующий функцию обратную заданной.
Так, например, для синтеза интегратора в обратную связь операционного усилителя (рис. 3) можно включить электрическую емкость (конденсатор), играющую роль дифференцирующего звена
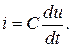
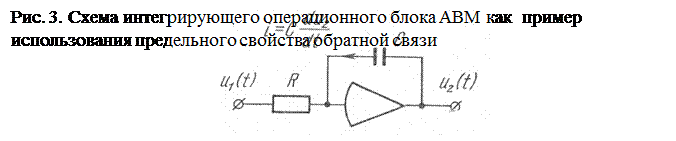
С учетом свойств операционного усилителя, в том числе 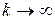 , можно легко показать, что такая система, представленная на рис. 3, описывается уравнением:
, можно легко показать, что такая система, представленная на рис. 3, описывается уравнением:
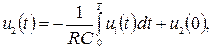 (12)
(12)
где RC — постоянная времени интегрирования;
u2(0) — начальное условие.
Аналогичным образом можно построить и другие решающие элементы.
К сожалению, для большинства реальных систем автоматического регулирования воспользоваться этим замечательным свойством не представляется возможным, так как реальные объекты и системы имеют, как правило, весьма ограниченные коэффициенты усиления и скорости перемещения регулирующего органа, а также обладают значительным запаздыванием. В связи с этим при аналитическом конструировании законов регулирования обычно пользуются соотношением (9) или (10), в которые входит передаточная функция (модель) объекта. Таким образом, даже задача синтеза относительно простой одноконтурной системы автоматического регулирования требует знания модели объекта.
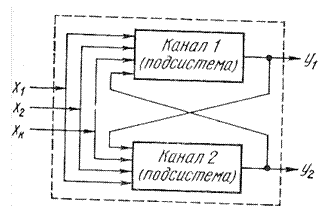 |
Еще большая необходимость в такой модели возникает при управлении многомерными объектами с внутренними перекрестными связями типа изображенного на рис. 4.

Можно выделить, по крайней мере, два подхода к управлению объектами такого рода.
1). Схема связанного регулирования, при которой между регуляторами отдельных величин устанавливают определенные перекрестные связи.
2.) Схема независимого регулирования (управления), при которой отсутствуют перекрестные связи между отдельными величинами, а выбор закона регулирования каждого регулятора осуществляется с учетом наличия перекрестных связей в объекте.
Для этого, естественно, необходима достаточно хорошая модель объекта, описывающая эти внутренние взаимосвязи. Наличие такой модели открывает возможность перехода на новую, более высокую ступень, когда можно вести речь уже не столько об автоматическом регулировании, сколько об автоматическом управлении, в том числе — оптимальном управлении в большом, так как путем оптимизационных расчетов или машинных экспериментов на быстрой модели здесь может решаться не только задача поддержания заданных траекторий каждой из выходных переменных (например у1 и у2), но и задача определения оптимальных траекторий, удовлетворяющих какому-либо целевому (технологическому или технико-экономическому) критерию, например минимуму затрат.
При том в ряде случаев может вообще отпасть необходимость в отдельных контурах стабилизирующего регулирования, а вместе с этим исчезает и возможность взаимных раскачивающих воздействий этих контуров друг на друга, значительно усложняющих расчеты устойчивости таких систем (систем связанного регулирования) и сами системы, поскольку появляется необходимость во введении различного рода ограничений и корректирующих контуров.
Остановимся более подробно на каждом из этих подходов.
Изображенная на рис. 5, схема связанного регулирования, является отражением первого подхода. Здесь два регулятора p1 и р2 превращаются по существу в один регулятор с двумя входами и выходами.
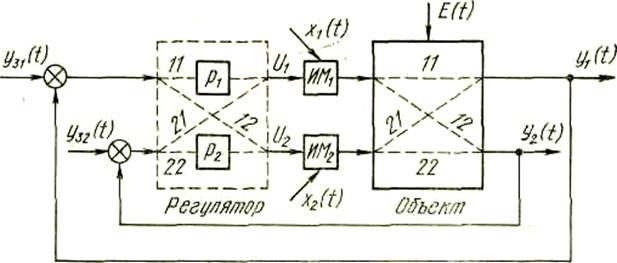
Рис. 5. Схема связанного регулирования
Его свойства определяются четырьмя операторами: двумя по прямым каналам 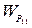 ,
, 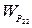 и двумя по перекрестным
и двумя по перекрестным 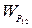 ,
, 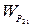 .
.
Для простоты наличием исполнительных механизмов ИМ1 и ИМ2 пренебрегаем, будем считать, что U1=x1(t); U2=x2(t).
Необходимо подчеркнуть, что особенностью рассматриваемого регулятора является одновременное перемещение обоих регулирующих органов при отклонении от задания y31(t), y32(t) хотя бы одной из регулируемых величин y1(t), y2(t), т. е. работа одного локального регулятора вносит возмущение в работу другого. Это и вызывает отмеченные несколько выше трудности при практической реализации таких систем.
Для синтеза оптимальной системы регулирования необходимо знать динамические характеристики объекта. Рассмотрим в общем виде структуру математического описания объекта для случая наличия хотя бы одного возмущения E(t). При этом математическая модель объекта должна включать в себя шесть динамических характеристик:
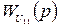 и
и 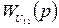 по каналам передачи первого регулирующего воздействия U1(t) соответственно на y1(t) и y2(t);
по каналам передачи первого регулирующего воздействия U1(t) соответственно на y1(t) и y2(t);
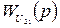 и
и 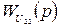 по каналам действия U2(t) соответственно на y1(t) и y2(t);
по каналам действия U2(t) соответственно на y1(t) и y2(t);
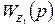 и
и 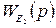 по каналам передачи первого регулирующего воздействия E(t) соответственно на y1(t) и y2(t).
по каналам передачи первого регулирующего воздействия E(t) соответственно на y1(t) и y2(t).
Целью синтеза является определение четырех оптимальных операторов регулятора 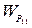 ,
, 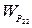 ,
, 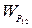 ,
, 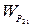 .
.
Следует заметить, что получить конкретные значения перечисленных динамических характеристик объекта, а за тем и операторов для связанных регуляторов весьма непросто даже для рассмотренного выше далеко не самого сложного случая. Ситуация может несколько упрощаться когда запаздывание по одному из каналов существенно меньше, чем по другому, тогда регулятор в первом канале начинает работать раньше чем в другом, и за счет этого может быть повышено качество регулирования. В большинстве же случаев синтез многосвязной системы регулирования является очень сложной задачей, особенно когда в объекте имеются внутренние перекрестные связи между выходами и входами, а управляющие и возмущающие воздействия являются общими для большинства каналов. Следует также иметь в виду возможность изменения характеристик объектов во времени или в зависимости от каких-либо условий.
Практически при технической реализации полученных указанным, выше способом алгоритмов работы многосвязных систем регулирования приходится вводить целый ряд ограничений, особенно с целью обеспечения устойчивости, так как наличие перекрестных связей в объекте и регуляторе приводит к появлению в системе большого числа дополнительных замкнутых контуров циркулирования воздействий, число которых может значительно превышать число регулируемых величин. При этом могут появляться в том числе и контуры с положительными обратными связями.
Рассмотренный выше подход является, как нетрудно заметить, дальнейшим развитием идей классической теории автоматического регулирования. Значительные трудности его практической реализации вызывают необходимость поиска принципиально иных подходов, одним из которых является определение оптимальных управляющих воздействий непосредственно на основе прогнозирующей модели объекта, отражающей внутренние связи в нем.
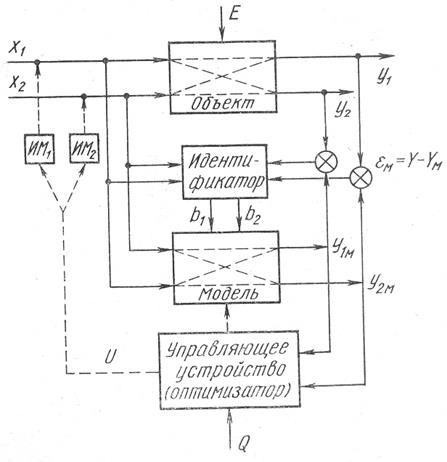
Одна из схем, относящаяся ко второму подходу в соответствии с принятой выше классификацией, представлена на рис. 6. Для лучшей сравнимости с предыдущей схемой (рис. 5) здесь также взяты две входных x1, х2 и две выходных переменных у1, у2, хотя в общем случае, естественно, их число может быть и большим. Аргумент t для простоты везде опущен.
 |
В основу работы системы, представленной на рис.6, положен выдвинутый известным советским ученым А. А. Фельдбаумом принцип дуального управления, нашедший дальнейшее развитие в управлении на основе обучаемой (подстраиваемой модели). Идея этого принципа заключается в следующем:
на каждом такте (этапе) управления сначала изучают объект (получают необходимые знания о нем),
а затем на основе этих знаний принимают решение о нанесении управляющих воздействий.
Остановимся подробнее на работе рассматриваемой схемы.
Информация о подаваемых на вход объекта расходах вещества или энергии (х1, х2 и т. д.) одновременно поступает также на входы модели и идентификатора. Выходы модели y1M, y2M сравниваются с выходами объекта y1 и y2.
Ошибки модели по каждому из каналов 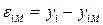 ,
, 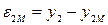 вместе с информацией о входах x1, х2 используются идентификатором для подстройки параметров модели (коэффициентов b1, b2 и т. д.).
вместе с информацией о входах x1, х2 используются идентификатором для подстройки параметров модели (коэффициентов b1, b2 и т. д.).
Например, для линейного случая векторное уравнение адаптивной идентификации имеет вид:
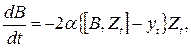
где Zt — вектор входов;
yt — выход;
В — вектор коэффициентов.
Выражение в фигурных скобках представляет собой невязку (ошибку модели). Интенсивность подстройки модели определяется коэффициентом α, зависящим в основном от статистических свойств помехи Е. Качество управления в рассматриваемой системе определяется прежде всего адекватностью структуры модели и ее параметров, что в свою очередь зависит от выбора алгоритма подстройки (адаптации).
Управляющее устройство (алгоритм), ориентируясь на заданный критерий (цель) оптимизации Q, осуществляет на модели машинный эксперимент (чаще всего с помощью одного из поисковых алгоритмов), направленный на определение значений управляющих воздействий (входов х1 и х2) и соответствующих им значений выходов y1; у2, удовлетворяющих заданному критерию оптимальности.
В простейшем случае задача может сводиться к поддержанию заданных значений выходов. Иногда возможно аналитическое преобразование модели объекта в управляющий алгоритм, но тогда мы по существу приходим к схеме, представленной на рис. 5.
Отличительной же особенностью рассматриваемого подхода (см. рис. 6) является разделение на два последовательных такта задач исследования объекта и управления им, что дает возможность наряду с решением задач управления получать знания о характеристиках объекта, что в свою очередь может быть использовано для дальнейшего совершенствования алгоритмов управления. При этом облегчается в необходимых случаях также диалоговый режим взаимодействия с оператором-технологом. Немаловажным преимуществом является возможность избежать дестабилизирующего воздействия отдельных каналов друг на друга, поскольку в рассматриваемой схеме управляющие воздействия на модели могут быть выбраны таким образом, чтобы они сразу удовлетворяли оптимальным траекториям всех выходов. В этом случае можно либо вообще обойтись без локальных контуров регулирования, реализуя полученные значения управлений непосредственно через исполнительные механизмы ИМ1, ИМ2, либо значительно облегчить работу этих контуров.
Таким образом, в рассмотренном подходе центр тяжести проблемы переносится в область создания адекватной модели, исследования и оптимизации объекта на ее основе. Именно этому будет посвящен следующий вопрос настоящей лекции.
Дата добавления: 2017-04-05; просмотров: 1244;











