Разложение функции отклика в степенной ряд, кодирование факторов
Если заранее не известно аналитическое выражение функции отклика, то можно рассматривать не саму функцию, а ее разложение, например, в степенной ряд в виде полинома
Y=В0 + B1Х1 + … + BnХn + В12Х1Х2 + … Вnn-1ХnХn-1 + В11Х12 + … + ВnnXn2 +…
Разложение в степенной ряд функции возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени.
Факторы могут иметь разные размерности (А, В, Вт, об/мин) и резко отличаться количественно. В теории планирования эксперимента используют кодирование факторов.
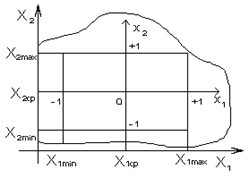
Рис. 5. Пространство кодированных факторов
Эта операция заключается в выборе нового масштаба для кодированных факторов (рис. 5), причем такого, чтобы минимальное значение кодированных факторов соответствовало “-1”, а максимальное значение “+1”, а также в переносе начала координат в точку с координатами
Х1ср, Х2ср, …, Хnср
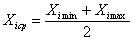 .
.
Текущее значение кодированного фактора
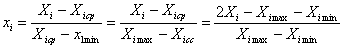 ,
,
где Хi – именованное (абсолютное) значение фактора; xi – кодированное значение фактора; Xicp -Ximin =Ximax-Xicp - интервал варьирования фактора.
Граница совместимости факторов указана на рис. 5 в виде кривой линии.
Если фактор изменяется дискретно, например он является качественным, то каждому уровню этого кодированного фактора присваиваются числа в диапазоне от +1 до –1. Так при двух уровнях это +1 и –1, при трех уровнях +1, 0, -1 и т.д.
Функция отклика может быть выражена через кодированные факторы Y=f(x1,…, хn) и записана в полиномиальном виде
Y=b0+b1х1+b2х2+…+bnхn+b12х1х2+…+bnn-1хn-1хn+b11х12+ …+bnnхn2+…
Очевидно, что 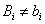 , но
, но
Y=F(X1,…, Xi,…, Xn) = f(x1,… xi,…, хn).
Для полинома, записанного в кодированных факторах, степень влияния факторов или их сочетаний на функцию отклика определяется величиной их коэффициента bi. Для полинома в именованных факторах величина коэффициента Вi еще не говорит однозначно о степени влияния этого фактора или их сочетаний на функцию отклика.
Степенной вид полинома может быть записан в более компактной форме
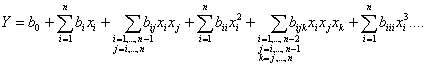 .
.
При определении общего числа членов степенного ряда количество парных сочетаний для n факторов в полиноме, тройных сочетаний, i-тых сочетаний 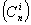 при n>i находится по соотношению
при n>i находится по соотношению
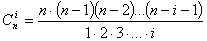 .
.
Например, для набора четырех чисел (n=4) - 1, 2, 3, 4 число тройных сочетаний составляет
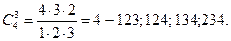
Если считать, что существует фактор х0 всегда равный 1, то
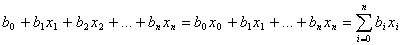 .
.
Если дополнительно все двойные, тройные и т.д. сочетания факторов, а также квадраты факторов и все соответствующие им коэффициенты обозначить через хi и bi, для i=n+1, …, m, то степенной ряд можно записать в виде
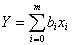 .
.
Здесь m+1 общее число рассматриваемых членов степенного ряда.
Для линейного полинома с учетом всех возможных сочетаний факторов
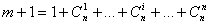 .
.
Полный квадратичный полином выглядит следующим образом:
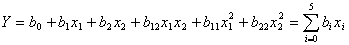 ,
,
где х0=1, х3=х1х2, х4=х12, х5=х22, b3=b12, b4=b11, b5=b22.
Матричные преобразования при обработке результатов эксперимента
При матричной записи результатов различных N опытов для полиномиального представления результата 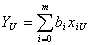 будем иметь
будем иметь
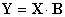 ; Х - матрица сочетаний факторов.
; Х - матрица сочетаний факторов.
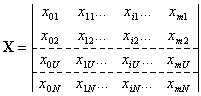
N строк
m+1 столбец.
Здесь 0,1, …,i,…, m – номера членов уравнения; 1,…,U,…,N … – номера опытов. Матрица Х - прямоугольная, содержащая m + 1 столбец и N строк.
Если учесть, что в матрице Х элементы 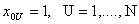 , то матрицу Х можно записать
, то матрицу Х можно записать
 .
.

Домножим левую и правую часть этого уравнения на одну и туже матрицу Xt – транспонированную матрицу Х
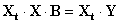 .
.
Транспонированная матрица – это матрица, у которой по отношению к исходной столбцы и строки поменяны местами.
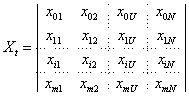
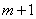 строка; N столбцов.
строка; N столбцов.
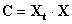 матрица, получившаяся в результате произведения транспонированной матрицы на исходную. Она является квадратной матрицей, содержащей m +1 строку и m + 1 столбец.
матрица, получившаяся в результате произведения транспонированной матрицы на исходную. Она является квадратной матрицей, содержащей m +1 строку и m + 1 столбец.
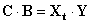 .
.
Для того чтобы получить в общем виде матрицу-столбец коэффициентов В необходимо домножить обе части последнего матричного уравнения слева на матрицу С-1 – матрицу обратную матрице С.
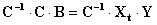 .
.
Обратная матрица строится так (используется процедура обращения матрицы), что при умножении ее на исходную матрицу получается единичная матрица – Е, у которой на главной диагонали расположены 1, а вне ее - 0.
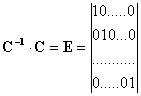 .
.
Окончательно в общем виде матрица-столбец коэффициентов полинома
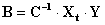 .
.
Рассмотрим в качестве простого примера полином в виде
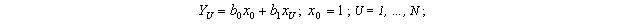
формируемого по результатам N опытов.
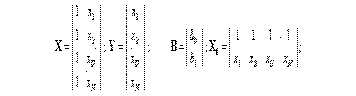
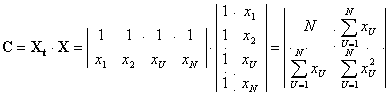 ;
;
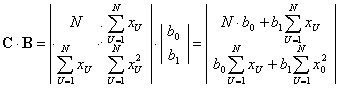 ;
;
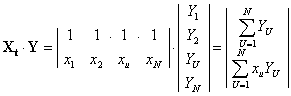 .
.
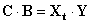 ;
;

Откуда решение системы относительно коэффициентов b0 и b1
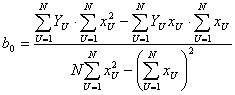 ,
,
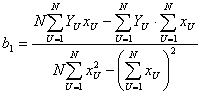 .
.
Этот результат полностью совпадает с соотношениями для такого же полинома при использовании метода наименьших квадрантов, где используется численный показатель минимальности суммы квадрантов отклонений во всех N опытах. Следовательно, построенный таким образом полином будет проходить самым ближайшим образом к результатам эксперимента.
Структура матрицы С играет важную роль в реализации алгоритма определения коэффициентов аппроксимирующего полинома. Структура матрицы С зависит от выбора значений факторов в N опытах, поэтому желательно особым образом выбирать значения факторов в опытах.
Элемент Сii на главной диагонали матрицы С (i-тая строка, i-тый столбец) представляется суммой квадратов значений i-того столбца сочетаний факторов матрицы Х в N опытах
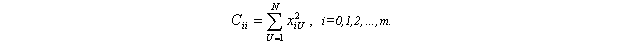
Элементы матрицы симметрично расположенные относительно главной диагонали равны между собой, то есть матрица С - симметричная.
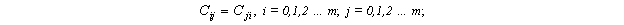
где первый индекс указывает номер столбца матрицы Х, второй индекс - номер строки.
При этом
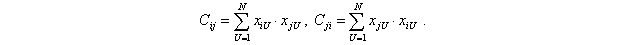
Чтобы существовала обратная матрица С-1, матрица С размера (1+m; 1+m) должна быть невырожденной, то есть ее определитель должен быть отличен от нуля. Это условие выполняется, если все m+1 столбцов матрицы Х линейно независимы. Кроме того, необходимо, чтобы число различных сочетаний факторов в матрице Х (число опытов N) должно быть не меньше чем m+1. Это условие исходит из того, что для определения m+1 коэффициентов полинома необходимо не менее m+1 уравнений (опытов).
Полученные коэффициенты B позволяют сформировать уравнение функции отклика при m+1 членах уравнения. Если точность этого уравнения оказалась недостаточной, то требуется взять уравнение с большим числом членов и начать все заново, так как все коэффициенты B оказываются зависимыми друг от друга. Это возникает при использовании пассивного эксперимента. Однако, если целенаправленно использовать активный эксперимент и особым образом построить матрицу сочетаний факторов в опытах Х, (использовать планирование эксперимента), то коэффициенты полинома определяются независимо друг от друга.
Стратегия применения планов заключается в принципе постепенного планирования – постепенного усложнения модели. Начинают с простейшей модели, т. е. находятся для нее коэффициенты, определяется ее точность. Если точность не удовлетворяет, то планирование и модель постепенно усложняются.
Задача планирования заключается в том, как нужно строить матрицу Х, чтобы матрица С легко обращалась и коэффициенты B определялись независимо друг от друга. Эти требования выполняется если матрица С является диагональной, то есть все элементы расположенные не на главной диагонали матрицы равны нулю
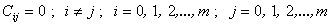 ;
;
или
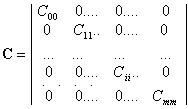 .
.
Тогда обратная матрица определяется как
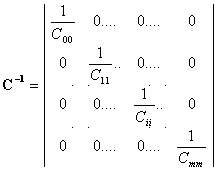 .
.
В этом случае система уравнений распадается на m+1 независимых уравнений и коэффициенты полинома определяются как
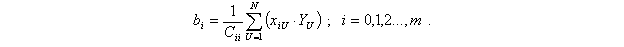
Если учесть, что Сii определяется как сумма квадратов значений факторов
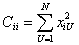 ,
,
то коэффициенты определяются как
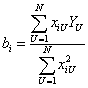
Требование выполнения условия 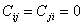 заключается в выполнении условия
заключается в выполнении условия
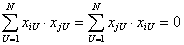 ,
,
где i, j - номера столбцов в матрице Х; 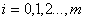 ;
; 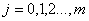 ; при
; при 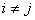 .
.
Каждый столбец матрицы Х можно представить в виде вектора
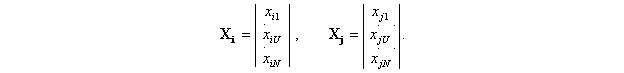
если 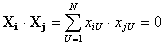 , то это означает что скалярное произведение двух векторов Хi и Хj равняется нулю, то есть векторы Хi и Хj - ортогональны.
, то это означает что скалярное произведение двух векторов Хi и Хj равняется нулю, то есть векторы Хi и Хj - ортогональны.
Так как любое скалярное произведение двух различных столбцов в матрице Х должно быть равно нулю, то это условие называется условием ортогональности матрицы Х, а соответствующее планирование эксперимента (определение сочетаний факторов) называется ортогональным планированием.
Для ортогонального планирования при учете того что 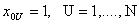
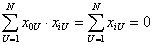 .
.
Таким образом, при ортогональном планировании сумма элементов любого столбца матрицы Х, кроме первого столбца должно быть равна нулю. Это правило используется при построении плана эксперимента, то есть при определении каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, эти уровни должны быть симметрично расположены относительно центральной точки х=0, при нечетном числе уровней должна использоваться и центральная точка (см. рис.6).
Кроме свойства ортогональности план может обладать свойствами насыщенности, рототабельности и др. План является насыщенным, если общее число опытов N равняется числу неизвестных коэффициентов полинома m+1.
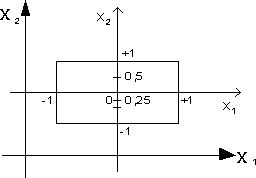
Рис. 6. Выбор уровней варьирования при ортогональном планировании
План называется рототабельным, если дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере).
Планы полного факторного эксперимента 2n (планы ПФЭ 2n)
Планы ПФЭ 2n являются простейшими планами первого порядка. Основание 2 означает, что принято два уровня варьирования, на которых фиксируются факторы, n – число факторов.
Для плана ПФЭ 22 число факторов равно двум (n=2) и число уровней фиксирования факторов также 2. Значения кодированных факторов выбираются в виде +1 и –1. Полное число возможных сочетаний значений n факторов (число опытов, а значит и число строк плана) N=22=4. Составляется план, в котором число столбцов факторов и их сочетаний равняется числу членов уравнения. Так для уравнения
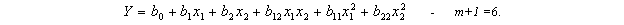
План ПФЭ 22 для этого уравнения представляется в следующем виде

В первый столбец (i=0) во все четыре ячейки заносятся +1. Во второй столбец (i=1) заносятся единицы с чередующими знаками (начинаем с -1). В этом случае сумма элемента столбца равняется нулю. Третий столбец заполняем единицами с чередующимися через 2 элемента знаками. Сумма элементов также равняется нулю. Геометрическое отображение плана ПФЭ 22 с указанием номеров точек плана в факторном пространстве представлено на рис. 7. Точки плана располагаются в вершинах квадрата.
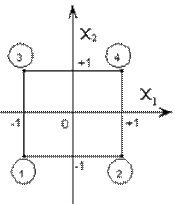
Рис. 7. Геометрическое отображение плана ПФЭ 22 в факторном пространстве
Элементы столбцов соответствующих произведениям факторов получаются путем перемножения элементов предыдущих столбцов. Такое правило позволяет гарантировать, что мы не пропустили ни одного возможного сочетания факторов в опытах и в то же время не будет повторений одинаковых сочетаний. Последние два столбца факторов, соответствующие квадратам факторов, состоят только из +1. Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбец х1х2, не обведенный утолщенной рамкой, при проведении опытов носит вспомогательный характер.
Особенности плана ПФЭ 22:
1. Различных столбцов в таблице получилось лишь четыре. Столбцы, соответствующие квадратам факторов неотличимы от столбца х0 - это общий результат для плана ПФЭ 2n. Это не позволяет определить отдельно коэффициенты при квадратах факторов. Поэтому планы ПФЭ 2n называют планами первого порядка. Для определения коэффициентов при квадратах факторов используют планы второго порядка. В дальнейшем в планах ПФЭ 2n столбцы квадратов факторов изображаться не будут.
2. Число различных столбцов равняется числу различных сочетаний факторов, то есть числу строк плана - числу опытов N. Это тоже общий результат для этих планов, то есть с помощью планов ПФЭ 2n можно определить все коэффициенты линейного полинома со всеми возможными сочетаниями факторов, включая коэффициенты b12…n , отражающие максимальное взаимодействие факторов вида х1х2…хn.
3. В плане ПФЭ 22 сумма квадратов элементов любого столбца
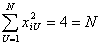 ,
,
Поэтому для планов ПФЭ 2n
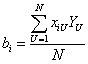 .
.
Таким образом, с помощью планов ПФЭ 2n можно определить свободный член уравнения b0, 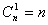 коэффициентов bi,
коэффициентов bi, 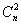 коэффициентов при различных взаимодействиях двух факторов bij ,
коэффициентов при различных взаимодействиях двух факторов bij , 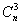 коэффициентов тройных взаимодействий факторов bijk , …..,
коэффициентов тройных взаимодействий факторов bijk , ….., 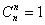 коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов
коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов
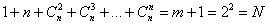 .
.
План ПФЭ 2n может являться насыщенным, при выборе числа членов уравнения m+1=N, ненасыщенным, при выборе числа членов уравнения и соответственно числа столбцов плана m+1<N . План ПФЭ 2n является также рототабельным, так как все точки плана лежат на окружности (сфере, гиперсфере) с радиусом 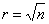 относительно центра плана.
относительно центра плана.
Для плана ПФЭ 23 число факторов n = 3. Выполняется N = 23 = 8 опытов. Уравнение может содержать до восьми членов
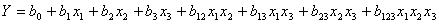 .
.
Таким образом, формируется план из восьми строк и восьми столбцов. В четвертом столбце (i=3) записываются единицы с чередующимися знаками через четыре элемента. План составляется аналогичным образом плану ПФЭ 22.
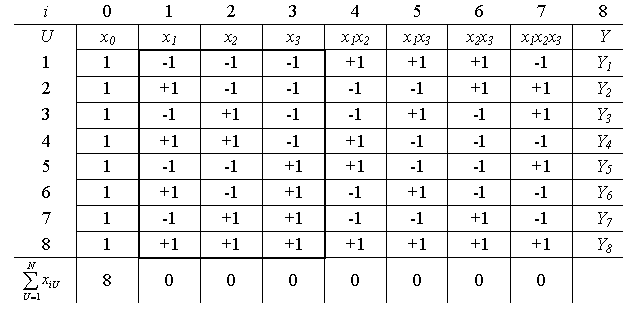
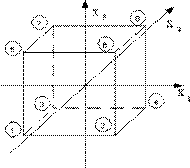
Рис. 8. Геометрическое отображение плана ПФЭ 23 в факторном пространстве
Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбцы, не обведенные утолщенной рамкой, при проведении опытов носят вспомогательный характер. Геометрическое отображение плана ПФЭ 23 с указанием номеров точек плана в факторном пространстве представлено на рис. 8. Точки плана располагаются в вершинах куба.
Пример применения плана ПФЭ 22. Пусть в результате проведения экспериментов по плану ПФЭ 22, то есть при изменении двух факторов, мы получили опытные значения Y1, Y2, Y3, Y4. Поверхность, уравнение которой нас интересует, имеет вид (см. рис. 9).
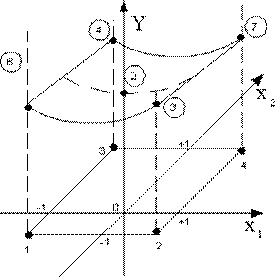
Рис. 9. Поверхность функции отклика
Составляем план ПФЭ 22.

Вначале найдем коэффициенты сокращенного линейного полинома вида
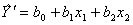
и результаты вычислений 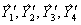 по нему.
по нему.
Рассчитываем коэффициенты полинома.
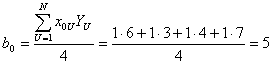 ;
;
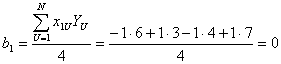 ;
;
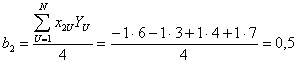 .
.
Полином имеет вид
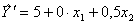 .
.
Результаты расчета по нему приведены в соответствующем столбце плана. Наблюдаются расхождения между Y и 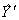 . Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида
. Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида
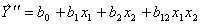 .
.
При этом ранее определенные коэффициенты остаются без изменений. Определим коэффициент при дополнительном члене полинома
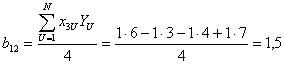 .
.
Полином имеет вид
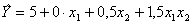 .
.
По нему рассчитываем предсказанные значения отклика в точках плана (столбец 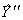 ). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана (
). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана ( 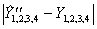 =0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1=0, х2=0), предсказанные и действительные значения, могут не совпадать (
=0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1=0, х2=0), предсказанные и действительные значения, могут не совпадать ( 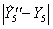 =3).
=3).
Планы второго порядка
Они позволяют сформировать функцию отклика в виде полного квадратичного полинома, который содержит большее число членов, чем неполный квадратичный полином, сформированный по планам первого порядка, и поэтому требуют большего числа выполняемых опытов. Полный квадратичный полином при n =2 содержит 6 членов
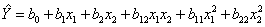 ,
,
при n = 3 - 11 членов
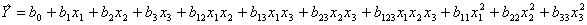 .
.
Известно, что для получения квадратичной зависимости каждый фактор должен фиксироваться как минимум на трех уровнях.
Для планов второго порядка область планирования может:
- Быть естественной, то есть включать область планирования планов первого порядка и дополнительные точки (такие планы называются композиционными). Дополнительные точки могут выходить за область плана первого порядка – единичного гиперкуба. В этом случае опыты в них реализуются при установлении факторов за пределами варьирования. Это надо учитывать при определении области совместимости факторов.
- Не выходить за пределы единичного гиперкуба, то есть для всех точек плана выполняется условие 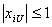 .
.
Не выходить за пределы единичного гипершара, определяемую соотношением таких значений факторов в плане, что 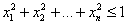 .
.
Во втором и третьем случаях используют специальные приемы выполнения приведенных соотношений в плане. План с одной областью планирования можно перестроить в план другой областью планирования.
Если уже был ранее сформирован план ПФЭ, но точность его функции отклика не удовлетворяет, то мы можем достроить этот план до плана второго порядка (композиционный план) и сформировать функцию отклика в виде полного квадратичного полинома, без потери информации о ранее сделанных опытах.
Ортогональный центрально-композиционный план второго порядка
Ортогональным планом называется такой план, у которого матрица планирования Х строится так, что бы матрица С=ХtХ оказалась диагональной. Используем этот подход и при построении планов второго порядка. План называется центральным, если все точки расположены симметрично относительно центра плана. ОЦКП – центральный симметричный ортогональный композиционный план.
В ОЦКП входят: ядро - план ПФЭ с N0= 2n точками плана, n0 (одна для этого плана) центральная точка плана 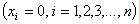 и по две “звездные” точки для каждого фактора
и по две “звездные” точки для каждого фактора
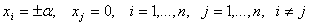 .
.
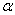 – плечо “звездных” точек.
– плечо “звездных” точек.
При этом в каждой плоскости, содержащей ось Y и координатную ось i-того фактора (проходящей через центр плана), оказываются три значения фактора хi 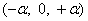 и три соответствующих значения Y.
и три соответствующих значения Y.
Общее количество точек в плане ОЦКП составляет
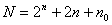 ,
,
где для ОЦКП n0=1.
При n > 2 в ОЦКП оказывается меньшее количество точек, чем в плане ПФЭ 3n .
Число точек в плане
| n | |||||
| ОЦКП | |||||
| ПФЭ 32 |
Графическое представление ОЦКП для n=3 приведено на рис. 13.
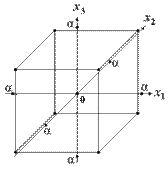
Рис. 13. ОЦКП при n=3
Для ортогонального плана необходимо, чтобы выполнялось соотношение
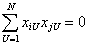 .
.
Так как 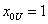 , то для столбцов j=1, 2,…., m+1 должно выполняться условие
, то для столбцов j=1, 2,…., m+1 должно выполняться условие
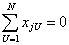 .
.
Это означает необходимость выполнения требования, чтобы сумма элементов любого столбца (кроме j=0), включая столбцы, соответствующие квадратам фактора, должна быть равна нулю. Это возможно, если члены столбцов, соответствующих квадратам факторов, преобразованы, иначе сумма квадратов факторов не может быть равна нулю.
Преобразование элементов этих столбцов осуществляется в виде
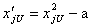 ,
,
где а – величина, зависящая от числа факторов.
Сумма элементов столбца, соответствующего квадратам факторов
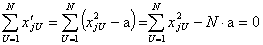 .
.
Откуда
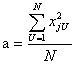 .
.
В общем случае ортогональный центрально-композиционный план при трех (n) факторов имеет следующий вид
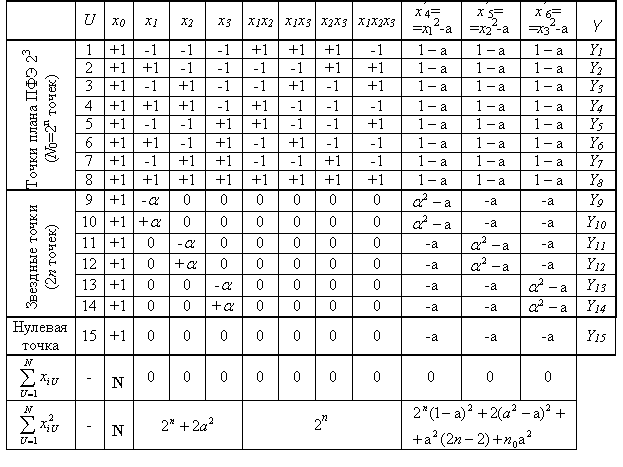
В ОЦКП каждый фактор фиксируется, в общем случае, на пяти уровнях
(- 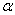 , -1, 0, 1, +
, -1, 0, 1, + 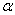 ).
).
Для определения неизвестных “а” и “ 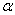 ” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов
” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов 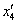 и
и 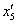
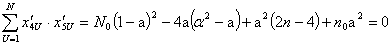 .
.
После простейших преобразований с учетом того, что 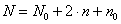 – общее число опытов в плане, получаем соотношение
– общее число опытов в плане, получаем соотношение
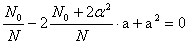 .
.
Соотношение для а при j=1, 2 или 3 может быть записано как (см. план)
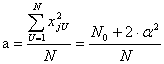 .
.
Подставив его в последнее уравнение, получаем
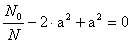 ,
,
откуда константа преобразования а
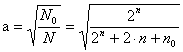 .
.
Тогда
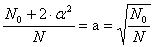
и плечо звездных точек
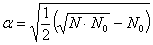 .
.
Например, для ОЦКП при числе факторов n=3 имеем следующие параметры плана
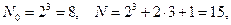
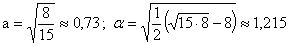 ,
,
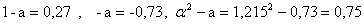 .
.
Сам план принимает вид
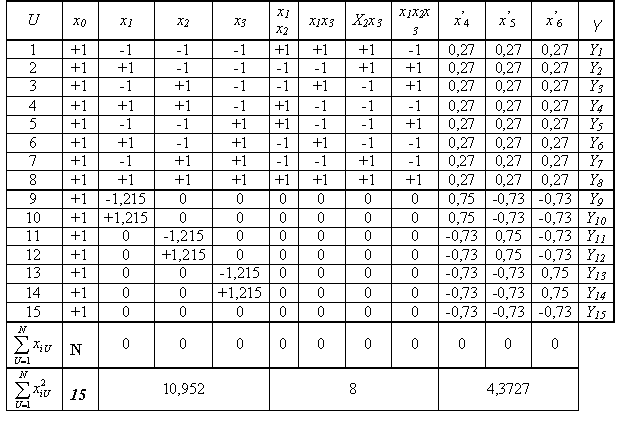
Очевидно, что план является ортогональным. В отличие от планов ПФЭ для ОЦКП сумма квадратов факторов разных столбцов не является одинаковой.
По результатам опытов плана формируется полином
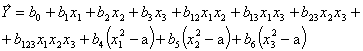 .
.
Коэффициенты полинома 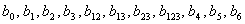 определяется как
определяется как
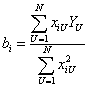 .
.
Можно преобразовать полином к виду
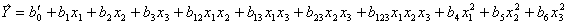 ,
,
где
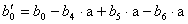 .
.
Значения параметров ОЦКП при числе факторов n

При n =2 ОЦКП совпадает с планом ПФЭ 23. Звездные точки ОЦКП в этом случае лежат на границах варьирования факторов. Если точки плана ПФЭ 2n всегда лежат на окружности (поверхности шара, гипершара), то точки плана ОЦКП не лежат на какой-либо одной окружности (поверхности шара, гипершара). План ОЦКП не является насыщенным. Так, например, для n = 3 полином имеет одиннадцать членов со своими коэффициентами, но для их определения используются пятнадцать опытов.
Пример плана ОЦКП для n = 2.
Параметры плана N0=4, N=9, 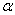 = 1, а = 2/3, 1-а=1/3, -а=-2/3,
= 1, а = 2/3, 1-а=1/3, -а=-2/3, 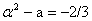 .
.
Использован рассмотренный ранее план ПФЭ 22 с добавленными опытами 5-9.
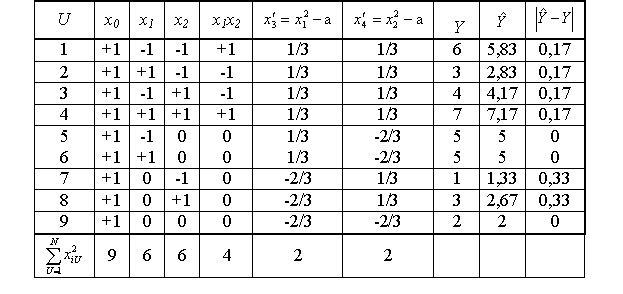
Коэффициенты полинома составляют
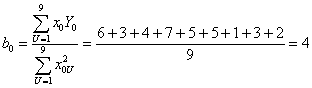 ;
;
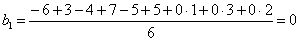 ;
;
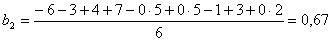 ;
;
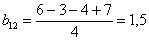 ;
;
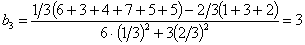 ;
;
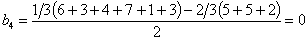 .
.
Полином принимает вид
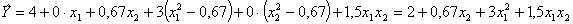 .
.
Ранее по плану ПФЭ 22 был сформирован полином 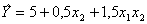 .
.
Рассчитанные значения 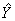 по полиному приведены в плане. Также приведены величины
по полиному приведены в плане. Также приведены величины 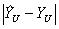 , подтверждающие достаточно высокую точность полинома. Так в центральной точке плана, в отличие от случая применения плана ПФЭ 22, расхождений нет.
, подтверждающие достаточно высокую точность полинома. Так в центральной точке плана, в отличие от случая применения плана ПФЭ 22, расхождений нет.
| <== предыдущая лекция | | | следующая лекция ==> |
| Диплоидное число хромосом | | | Общие понятия математического моделирования процессов в машиностроении |
Дата добавления: 2017-04-05; просмотров: 2349;











