Общие понятия математического моделирования процессов в машиностроении
Под объектами моделирования в машиностроительном производстве следует понимать:
1. Технологические системы (ТС) – участки из универсальных станков, автоматические линии, гибкие производственные системы (ГПС).
2. Технологические процессы (ТП).
3. Физические процессы (ФП) – процессы, протекающие при резании металлов, при функционировании технологического оборудования в упругой системе СПИД и т.д.
Математические модели ТП будут подробно рассмотрены в курсе «САПР ТП». В данном курсе рассматриваются математические модели технологических систем и физических процессов.
В чистом виде (по – отдельности) математические модели данных объектов применяются редко, как правило, они комбинированные. Например, в математических моделях ТС используются математические модели ТП, в которых, в свою очередь, применяются математические модели ФП.
Математическая модель объекта моделирования – это система математических элементов (чисел, переменных, уравнений, неравенств, множеств, матриц, графов и т.д.) и отношений между ними, адекватно отражающая некоторые свойства объекта, существенные с точки зрения инженера, для решения той или иной задачи.
Математические модели разрабатываются для:
1. Описания ФП, ТП, ТС.
2. Исследования ФП, ТП, ТС.
3. Проектирования ТП, ТС.
4. Оптимизации в ходе проектирования ТП, ТС и организации работы ТС.
5. Построения систем автоматизированного проектирования.
Вид, состав, сложность математической модели зависит от того, какой объект она описывает и для каких целей разработана.
Пример 1. Пусть требуется описать и исследовать процесс резания (точения) с точки зрения действующих сил, которые представим известными в теории резания уравнениями:
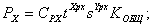
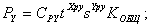
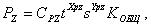
где 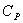 – удельные силы резания;
– удельные силы резания;
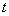 – глубина резания;
– глубина резания;
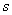 – подача;
– подача;
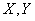 – показатели степени, выражающие влияние соответствующего параметра режима резания на силу резания ( при точении
– показатели степени, выражающие влияние соответствующего параметра режима резания на силу резания ( при точении 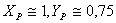 );
);
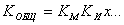 - коэффициент, зависящий от свойств обрабатываемого материала, инструментального материала и т.д.
- коэффициент, зависящий от свойств обрабатываемого материала, инструментального материала и т.д.
Представленные выше три уравнения – это уже один из вариантов математической модели процесса точения с точки зрения действующих сил. Она, конечно же, простейшая и может служить для :
1. Описания процесса резания.
2. Исследования процесса резания.
3. Расчета сил резания.
Например, с помощью данной модели можно исследовать зависимость силы резания 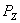 от глубины резания
от глубины резания 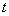 ( рис.1.1)
( рис.1.1)
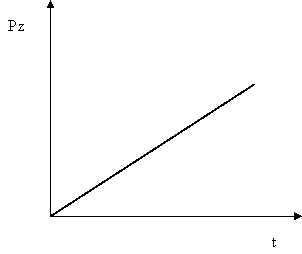
Рис.1.1. Зависимость силы резания Pz от глубины резания t
Использовать математическую модель процесса резания в таком виде, например, для проведения оптимизации режимов резания нельзя, она слишком проста. Для оптимизации математическая модель должна иметь следующие элементы:
1. Критерий или критерии оптимизации.
2. Целевую функцию.
3. Систему ограничений.
4. Систему уравнений, описывающих объект.
5. Входные, выходные и внутренние параметры.
6. Управляемый (варьируемый) или управляемые (варьируемые) параметры, которые выделяются из числа внутренних параметров.
Пример 2. Однопараметрическая однокритериальная оптимизация режимов резания.
Пусть требуется определить оптимальную подачу 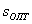 , при этом глубина резания постоянна (
, при этом глубина резания постоянна ( 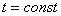 ).
).
1. Критерий оптимизации - сила резания 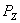 .
.
2. Целевая функция – зависимость между критерием (критериями) оптимизации и подлежащими оптимизации параметрами с указанием направления (вида) экстремума. В нашем примере она имеет следующий вид:
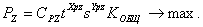
3. Система ограничений включает в себя лишь одно из них:
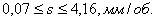
4. Система уравнений. Математическая модель в нашем примере включает в себя одно уравнение
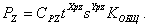
5. Входные параметры – 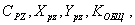
o выходной параметр – 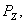
o внутренние параметры – 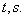
6. Управляемый (варьируемый) параметр – 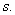
Задача оптимизации решается в два этапа (см. рис.1.2):
Этап 1. Определение области допустимости решений (работаем с ограничениями) – ОДР.
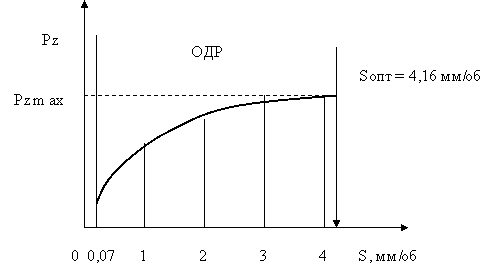
Рис. 1.2. Графическая иллюстрация решения задачи оптимизации
Этап 2. Определение оптимального параметра – 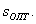
В общем виде математическая модель объекта записывается:
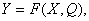
где 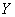 – вектор выходных параметров,
– вектор выходных параметров, 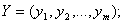
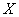 – вектор внутренних параметров,
– вектор внутренних параметров, 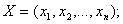
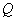 – вектор внешних (входных) параметров,
– вектор внешних (входных) параметров, 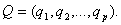
Для приведенной выше математической модели процесса резания:
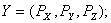
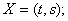
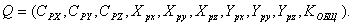
Следует иметь в виду, что любой объект не может существовать обособленно, без взаимосвязи с другими объектами (окружающей средой). Для процесса резания элементами окружающей среды являются обрабатываемый и инструментальный материалы, смазочно-охлаждающая жидкость, образующаяся в результате обработки стружка и т.д. Для технологического процесса в ходе его реализации - это технологическое оборудование, режущий инструмент, элементы приспособления и т.д. Для технологической системы (механического участка из универсальных станков или станков с ЧПУ, автоматической линии и др.) элементами окружающей среды являются другие технологические системы, цеховой транспорт и т.д.
Структурная схема объекта моделирования представлена на рис.1.3.

Рис.1.3. Структурная схема объекта моделирования
Лекция 2
Классификация математических моделей.
Требования, предъявляемые к математическим моделям
Классификация математических моделей
Классификация в любой области знаний чрезвычайно важна. Она позволяет обобщить накопленный опыт, упорядочить понятия предметной области. Не является исключением в этом смысле и математическое моделирование. В табл.2.1 показаны виды математических моделей по различным признакам классификации.
Таблица 2.1 Классификация математических моделей
| Признаки классификации | Виды математических моделей |
| 1. Принадлежность к иерархическому уровню | 1. Модели микроуровня 2. Модели макроуровня 3. Модели метауровня |
| 2. Характер отображаемых свойств объекта | 1. Структурные 2. Функциональные |
| 3. Способ представления свойств объекта | 1. Аналитические 2. Алгоритмические 3. Имитационные |
| 4. Способ получения модели | 1. Теоретические 2. Эмпирические |
| 5. Особенности поведения объекта | 1. Детерминированные 2. Вероятностные |
Приведенная классификация математических моделей может быть применена по отношению к любым объектам. Мы рассмотрим особенности различных видов моделей применительно к объектам (процессам) в машиностроении.
Математические модели на микроуровнепроизводственного процесса отражают физические процессы, протекающие, например, при резании металлов. Они описывают процессы на уровне перехода (прохода).
Математические модели на макроуровне производственного процесса описывают технологические процессы.
Математические модели на метауровне производственного процесса описывают технологические системы (участки, цехи, предприятие в целом).
Структурные математические модели предназначены. для отображения структурных свойств объектов. Например, в САПР ТП для представления структуры технологического процесса, расцеховки изделий используется структурно – логические модели.
Функциональные математические модели предназначены для отображения информационных, физических, временных процессов, протекающих в работающем оборудовании, в ходе выполнения технологических процессов и т.д.
Аналитические математические модели представляют собой явные математические выражения выходных параметров как функций от параметров входных и внутренних. Это, например, выражения для сил резания в примерах, приведенных в лекции 1. Ввиду того, что нами будет рассматриваться далее целый ряд аналитических моделей, поговорим о них более подробно.
Аналитическое моделирование основано на косвенном описании моделируемого объекта с помощью набора математических формул. Язык аналитического описания содержит следующие основные группы семантических элементов: критерий (критерии), неизвестные, данные, математические операции, ограничения. Наиболее существенная характеристика аналитических моделей заключается в том, что модель не является структурно подобной объекту моделирования. Под структурным подобием здесь понимается однозначное соответствие элементов и связей модели элементам и связям моделируемого объекта. К аналитическим относятся модели, построенные на основе аппарата математического программирования, корреляционного, регрессионного анализа. Аналитическая модель всегда представляет собой конструкцию, которую можно проанализировать и решить математическими средствами. Так, если используется аппарат математического программирования, то модель состоит в основе своей из целевой функции и системы ограничений на переменные. Целевая функция, как правило, выражает ту характеристику объекта (системы), которую требуется вычислить или оптимизировать. В частности, это может быть производительность технологической системы. Переменные выражают технические характеристики объекта (системы), в том числе варьируемые, ограничения – их допустимые предельные значения.
Аналитические модели являются эффективным инструментом для решения задач оптимизации процессов, протекающих в технологических системах, а также оптимизации и вычисления характеристик самих технологических систем.
Важным моментом является размерность конкретной аналитической модели. Часто для реальных технологических систем (автоматических линий, гибких производственных систем) размерность их аналитических моделей столь велика, что получение оптимального решения оказывается весьма сложным с вычислительной точки зрения. Для повышения вычислительной эффективности в этом случае используют различные приемы. Один из них связан с разбиением задачи большой размерности на подзадачи меньшей размерности так, чтобы автономные решения подзадач в определенной последовательности давали решение основной задачи. При этом возникают проблемы организации взаимодействия подзадач, которые не всегда оказываются простыми. Другой прием предполагает уменьшение точности вычислений, за счет чего удается сократить время решения задачи.
Алгоритмические математические модели выражают связи между выходными параметрами и параметрами входными и внутренними в виде алгоритма.
Имитационные математические модели – это алгоритмические модели, отражающие развитие процесса (поведение исследуемого объекта) во времени при задании внешних воздействий на процесс (объект). Например, это модели систем массового обслуживания, заданные в алгоритмической форме.
Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, что каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними.
Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента.
Ценным качеством имитации является возможность управлять масштабом времени. Динамический процесс в имитационной модели протекает в так называемом системном времени. Системное время имитирует реальное время. При этом пересчет системного времени в модели можно выполнять двумя способами. Первый способ заключается в «движении» по времени с некоторым постоянным шагом. Второй способ заключается в «движении» по времени от события к событию, при этом считается, что в промежутках времени между событиями в модели изменений не происходит.
Теоретические математические модели создаются в результате исследования объектов (процессов) на теоретическом уровне. Например, существуют выражения для сил резания, полученные на основе обобщения физических законов. Но они не приемлемы для практического использования, т.к. очень громоздки и не совсем адаптированы к реальным процессам обработки материалов.
Эмпирические математические модели создаются в результате проведения экспериментов (изучения внешних проявлений свойств объекта с помощью измерения его параметров на входе и выходе) и обработки их результатов методами математической статистики.
Детерминированные математические модели описывают поведение объекта с позиций полной определенности в настоящем и будущем. Примеры таких моделей: формулы физических законов, технологические процессы обработки деталей и т.д.
Вероятностные математические модели учитывают влияние случайных факторов на поведение объекта, т.е. оценивают его будущее с позиций вероятности тех или иных событий. Примеры таких моделей: описание ожидаемых длин очередей в системах массового обслуживания, ожидаемых объемов выпуска сверхплановой продукции производственным участком, точности размеров в партии деталей с учетом явления рассеяния и т.д.
Требования, предъявляемые к математическим моделям
К математическим моделям предъявляются следующие основные требования:
1. Универсальности.
2. Точности.
3. Адекватности.
4. Экономичности.
Универсальность математической модели характеризует полноту отражения в ней свойств реального объекта. Математическая модель отражают не все, а лишь некоторые свойства реального объекта. Например, формулы для сил резания, которые приведены в лекции 1 , не учитывают температуру окружающего воздуха, влажность, экономические параметры и т.д.
Точность математической модели оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели.
Пусть отражаемые в математической модели свойства объекта оцениваются вектором выходных параметров 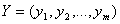 ,
, 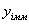 - i-ый параметр, рассчитанный с помощью модели, а
- i-ый параметр, рассчитанный с помощью модели, а 
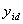 - истинное значение того же параметра. Тогда относительная погрешность математической модели по i – му параметру будет равна:
- истинное значение того же параметра. Тогда относительная погрешность математической модели по i – му параметру будет равна:

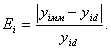
По этой формуле рассчитываются погрешности для каждого выходного параметра, в результате получается вектор погрешностей 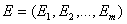 . В целом для математической модели погрешность оценивается следующим образом:
. В целом для математической модели погрешность оценивается следующим образом:
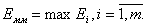
Например, оценим погрешность рассмотренной в лекции 1 математической модели. Вектор выходных параметров 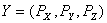 . Пусть
. Пусть 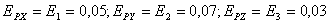 ; тогда в целом погрешность математической модели
; тогда в целом погрешность математической модели 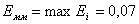 .
.
Адекватность математической модели – это ее способность отражать заданные свойства объекта с погрешностью, не выше заданной.
Т. к. выходные параметры модели являются функцией 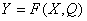 от параметров внутренних и входных, то и точность модели зависит от их значений. Адекватность модели имеет место в ограниченной области изменения внутренних и входных параметров. Если обозначить область адекватности как
от параметров внутренних и входных, то и точность модели зависит от их значений. Адекватность модели имеет место в ограниченной области изменения внутренних и входных параметров. Если обозначить область адекватности как 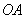 , то
, то
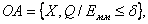
где 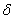 - некоторое заданное число.
- некоторое заданное число.
Экономичность математической модели характеризуется затратами вычислительных ресурсов на ее реализацию. Если работа с математической моделью осуществляется вручную, то ее экономичность определяется затратами личного времени проектировщика. Если модель используется при автоматизированном проектировании, то затратами машинного времени и памяти компьютера. Так как указанные величины определяются характеристиками конкретного компьютера, то использовать их для оценки экономичности математической модели не корректно. Поэтому, для оценки экономичности самой математической модели используют другие величины:
1. Среднее количество операций, выполняемых при одном обращении к математической модели.
2. Размерность системы уравнений в математической модели.
3. Количество используемых в модели внутренних параметров и т.д.
Требования высокой степени универсальности, точности, широкой области адекватности математической модели, с одной стороны, и высокой ее экономичности, с другой стороны, противоречивы. Поэтому компромиссные решения определяются решаемой задачей.
К математическим моделям предъявляется и целый ряд других требований, среди которых следует выделить следующие:
1. Вычислимость, т.е. возможность ручного или с помощью ЭВМ исследования качественных и количественных закономерностей функционирования объекта (системы).
2. Модульность, т.е. соответствие конструкций модели структурным составляющим объекта (системы).
3. Алгоритмизируемость, т.е. возможность разработки соответсвующих алгоритма и программы, реализующей математическую модель на ЭВМ.
4. Наглядность, т.е. удобное визуальное восприятие модели.
Лекция 3
Основы теории множеств и теории графов
Множество – это объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью (автор определения – основатель теории множеств Кантор).
Пусть 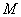 – множество.
– множество.
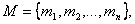
где 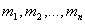 – элементы множества.
– элементы множества.
Применяются следующие выражения:
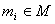 – элемент
– элемент 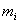 принадлежит множеству
принадлежит множеству 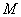 ;
;
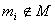 – элемент
– элемент 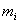 не принадлежит множеству
не принадлежит множеству 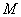 ;
;
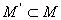 –
– 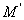 является подмножеством множества
является подмножеством множества 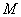 .
.
Декартовым (прямым) произведением двух множеств 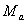 и
и 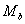 называется множество вида:
называется множество вида:
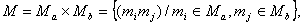
где 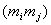 – упорядоченное множество, в котором задан порядок элементов.
– упорядоченное множество, в котором задан порядок элементов.
Пример 1. Даны два множества 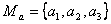 и
и 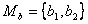 . Декартовым произведением этих множеств будет множество
. Декартовым произведением этих множеств будет множество
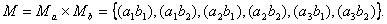
Количество элементов декартового произведения определяется следующим образом (для нашего примера):

Квадратом множества 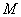 называется декартовое произведение двух равных между собой множеств:
называется декартовое произведение двух равных между собой множеств:
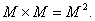
Бинарным отношением 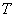 в множестве
в множестве 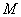 называется подмножество его квадрата.
называется подмножество его квадрата.
Пример 2. Пусть 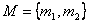 . Квадрат этого множества запишется:
. Квадрат этого множества запишется:
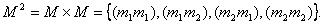
Бинарным отношением в этом множестве является, например, следующее:
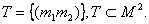
Совокупность множества 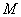 с заданным в нем бинарным отношением
с заданным в нем бинарным отношением 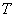 называется графом
называется графом 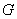 .
.
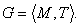
Любой граф можно представить в виде матрицы смежности графа. Для рассмотренного выше примера 2 матрица будет иметь следующий вид:
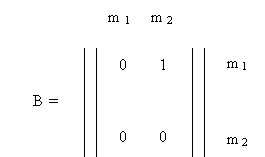
В этой матрице 1 – обозначает наличие связей между элементами множества, 0 – отсутствие связей между элементами множества.
Примечание: матрицы будем читать по принципу «строка – столбец».
Для нашего примера граф будет иметь следующий вид (рис.3.1):
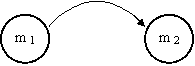

Рис 3.1. Граф для примера 2
Две встречные дуги в графе могут быть заменены линией без стрелок на концах. Эта линия называется ребром графа (рис. 3.2).
Матрицы смежности обоих графов, представленных на рис 3.2., имеют вид:
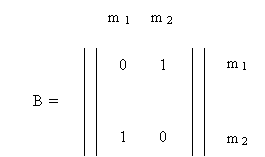
Пример 3. Пусть требуется изобразить граф, представленный следующей матрицей смежности:
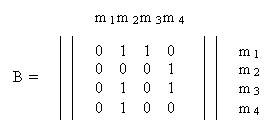
Граф, соответствующий этой матрице, изображен на рис. 3.3.
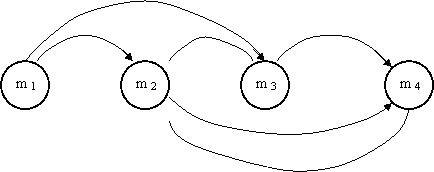
Рис. 3.3. Граф для примера 3
Пример 4. Имеется эскиз детали, представленный на рис.3.4.
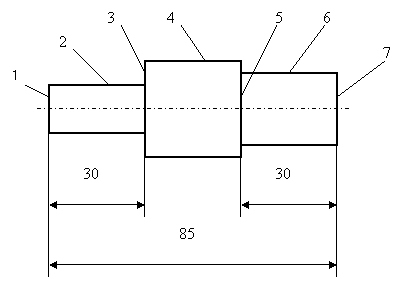
Рис. 3.4. Эскиз детали для примера 4
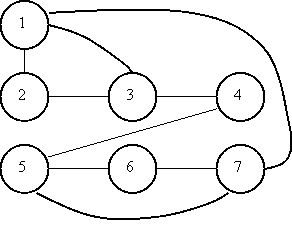
Рис.3.5. Граф для примера 4
Требуется изобразить в виде графа и матрицы смежности конструктивные и размерные связи этой детали.
Граф для этого примера изображен на рис. 3.5.
На рис. 3.5 конструктивные связи детали изображены (тонкими линиями) в виде ребер графа, т.к. здесь безразлично, связана, например, конструктивно поверхность 2 с поверхностью 3 или наоборот (они просто связаны между собой). Размеры также проставлены между поверхностями, в этом примере нет приоритета, какая из поверхностей является базой при обработке детали. Поэтому и размерные связи изображены (толстыми линиями) в виде ребер, а не дуг графа. Если же важно будет указать, что одна поверхность является базовой, а положение другой задано относительно ее, то в графе связь между этими поверхностями следует изобразить в виде дуги, исходящей из вершины, отождествляющей первую поверхность и входящей в вершину, отождествляющую вторую поверхность.
Матрица смежности данного графа имеет следующий вид:

Лекция 4
Общая постановка и виды задач принятия решений.
Математическая постановка и разрешимость задач оптимизации
При проектировании любых технических объектов, технологических процессов и систем всегда решаются задачи выбора и принятия решений.
Задачей принятия решения называют кортеж (совокупность) 

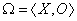 ,
,
где 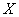 – множество вариантов решения задачи;
– множество вариантов решения задачи;
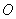 – принцип оптимальности, дающий представление о качестве вариантов, в простейшем случае – это правило их предпочтения друг перед другом.
– принцип оптимальности, дающий представление о качестве вариантов, в простейшем случае – это правило их предпочтения друг перед другом.
Решением задачи принятия решений называется множество 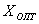 , которое является подмножеством множества
, которое является подмножеством множества 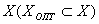 , полученное на основе принципа оптимальности.
, полученное на основе принципа оптимальности.
Задачи принятия решений классифицируются по наличию информации об 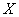 и
и 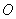 и бывают трех видов:
и бывают трех видов:
1. 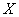 и
и 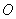 – неизвестны. Это общая задача принятия решений. Данные для получения xопт определяют в данной задаче в процессе ее решения.
– неизвестны. Это общая задача принятия решений. Данные для получения xопт определяют в данной задаче в процессе ее решения.
2. 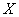 – неизвестно,
– неизвестно, 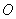 – известно ( эта задача поиска вариантов).
– известно ( эта задача поиска вариантов).
3. 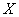 и
и 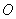 – известны ( это задача оптимизации).
– известны ( это задача оптимизации).
В общем случае задача принятия решения решается в два этапа:
1 этап: Задача формализуется, т.е. строится ее математическая модель, в которой конкретные физические, технические, технологические, экономические условия и требования к объекту воплощаются в виде задачи оптимизации с определенной целевой функцией и допустимым множеством вариантов.
2 этап: Решение задачи оптимизации с использованием известных методов.
Основы теории оптимизации
«Теория оптимизации», с одной стороны, является самостоятельной наукой, а, с другой стороны, составной частью науки под названием «исследование операций».
Операция (в данной науке) – это совокупность взаимосогласованных действий, направленных на достижение вполне определенной цели.
Обязательно должно быть сформулирована цель. Если есть разные пути достижения этой цели, то необходимо найти наилучший из них.
Математическая постановка задачи оптимизации
Постановка задачи оптимизации включает в себя множество допустимых решений 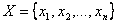 и числовую функцию
и числовую функцию 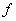 , определенную на этом множестве, которая называется целевой функцией.
, определенную на этом множестве, которая называется целевой функцией.
Нельзя отождествлять критерий (критерии) оптимальности и целевую функцию.
Целевая функция – это аналитическая зависимость между критерием (критериями) оптимальности и подлежащими оптимизации параметрами с указанием направления экстремума.
Отличие понятий «критерий» и «целевая функция» состоит в следующем:
1. Целевая функция может включать в себя более одного критерия.
2. Для целевой функции всегда и обязательно указывается вид экстремума:
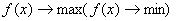 .
.
Различают два вида задач оптимизации:
1. Задачу минимизации.
2. Задачу максимизации.
Чтобы решить задачу минимизации функции 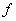 на множестве
на множестве 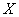 , необходимо найти такой вектор
, необходимо найти такой вектор 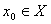 ( а также соответствующее значение целевой функции
( а также соответствующее значение целевой функции 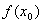 ), чтобы неравенство:
), чтобы неравенство: 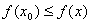 выполнялось для всех
выполнялось для всех 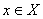 . При этом
. При этом 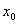 называют оптимальным решением (точнее здесь – минимальным решением),а
называют оптимальным решением (точнее здесь – минимальным решением),а 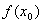 - оптимумом (минимумом).
- оптимумом (минимумом).
Чтобы решить задачу максимизации функции 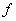 на множестве
на множестве 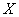 , необходимо найти такой вектор
, необходимо найти такой вектор 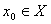 ( а также соответствующее значение целевой функции
( а также соответствующее значение целевой функции 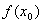 ), чтобы неравенство:
), чтобы неравенство: 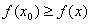 выполнялось для всех
выполнялось для всех 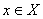 . При этом
. При этом 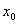 называют оптимальным (максимальным ) решением, а
называют оптимальным (максимальным ) решением, а 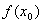 – оптимумом ( максимумом ).
– оптимумом ( максимумом ).
В общем виде находится именно вектор 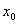 , т.к., например, при решении двухпараметрической задачи, он будет включать в себя два параметра, трехпараметрической – три параметра и т.д.
, т.к., например, при решении двухпараметрической задачи, он будет включать в себя два параметра, трехпараметрической – три параметра и т.д.
Локальный и глобальный минимум (максимум) целевой функции
При решении задач оптимизации следует иметь в виду, какой вид имеет целевая функция.
Например, 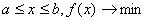 . Целевая функция имеет вид, как показано на рис. 4.1.
. Целевая функция имеет вид, как показано на рис. 4.1.
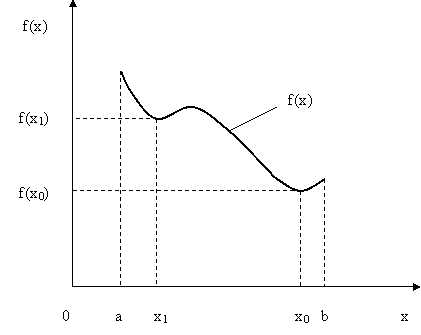
Рис.4.1. Иллюстрация понятий «локальный минимум» и «глобальный минимум» целевой функции
Здесь т. 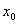 - глобальный минимум, а т.
- глобальный минимум, а т. 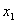 - локальный минимум целевой функции.
- локальный минимум целевой функции.
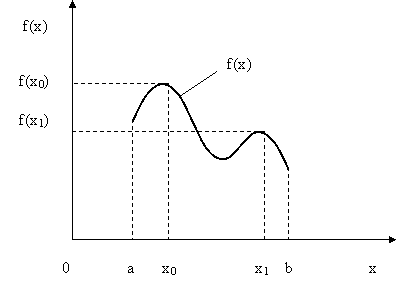
Рис.4.2. Иллюстрация понятий «локальный максимум» и «глобальный максимум» целевой функции
Пусть теперь 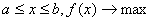 , а целевая функция имеет вид, как показано на рис.4.2.
, а целевая функция имеет вид, как показано на рис.4.2.
Здесь 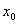 - точка глобального максимума, а
- точка глобального максимума, а 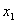 - точка локального максимума целевой функции.
- точка локального максимума целевой функции.
Разрешимость задач оптимизации
Приведенная выше задача оптимизации имеет решение не при любых целевых функциях и допустимых множествах. Существуют задачи, в которых невозможно найти оптимальное решение и экстремум целевой функции. Например, не существует точек минимума функции одной переменной 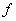 на множестве
на множестве 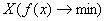 в случаях, приведенных ниже на рис. 4.3, 4.4 и 4.5.
в случаях, приведенных ниже на рис. 4.3, 4.4 и 4.5.
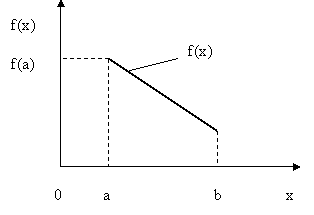
Рис.4.3. Иллюстрация случая, когда множество допустимых решений не замкнуто
Здесь граница «а» множества допустимых решений в интервал входит, а граница «b» нет.
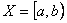 - множество
- множество 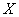 не замкнуто, следовательно,
не замкнуто, следовательно, 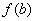 – не существует.
– не существует.
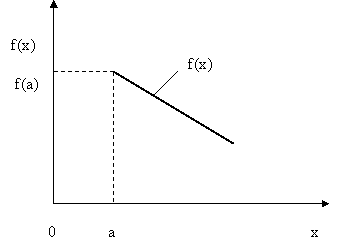
Рис.4.4. Иллюстрация неограниченности множества допустимых решений
В случае, представленном на рис.4.4, определена лишь одна левая граница множества допустимых решений. 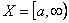 , т.е. множество допустимых решений неограниченно.
, т.е. множество допустимых решений неограниченно.
На рис.4.5. показан еще один случай, когда задача оптимизации не имеет однозначного решения.
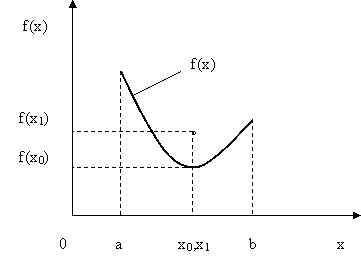
Рис.4.5. Иллюстрация случая, когда функция f(x) не является непрерывной
Здесь функция 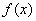 не является непрерывной, т.к. в т.
не является непрерывной, т.к. в т. 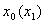 существуют два значения функции –
существуют два значения функции – 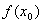 и
и 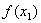 .
.
Следовательно, задача оптимизации разрешима, если выполняются следующие три условия:
1. Множество допустимых решений 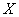 замкнуто, т.е. если предельные точки принадлежат этому множеству.
замкнуто, т.е. если предельные точки принадлежат этому множеству.
2. Множество 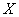 ограничено.
ограничено.
3. Целевая функция 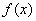 непрерывна.
непрерывна.
Это нестрогая формулировка теоремы Вейерштрасса.
Лекция 5
Графо – аналитический метод решения задач математического программирования
Задачами математического программирования называют однокритериальные задачи оптимизации. Методы их решения оперируют с детерминированными математическими моделями. Напомним, что детерминированная математическая модель отражает поведение объекта с позиций полной определенности в настоящем и будущем.
Эти модели в исследовании операций занимают одно из главных мест. Это обусловлено тем, что в них отражены разнообразные проблемы распределения ограниченных ресурсов в экономике, военном деле, создании новой техники и т.д. Пути решения этих проблем так или иначе связаны с планированием целенаправленной деятельности, т.е. с разработкой определенных установок на будущее.
Термин «программирование» (от английского «programming» - составление плана или программы действий) здесь следует понимать в смысле «поиск наилучших планов» (в отличие от того толкования, которое принято специалистами по программному обеспечению ЭВМ, – «составление программы для ЭВМ»).
Задача математического программированияформулируется следующимобразом: найти значения переменных 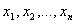 , доставляющие максимум (минимум) заданной целевой функции
, доставляющие максимум (минимум) заданной целевой функции 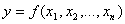 при условиях:
при условиях:

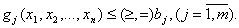
Различают два вида задач математического программирования:
1. Задачи линейного программирования.
2. Задачи нелинейного программирования.
В первых задачах функция 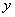 и ограничения
и ограничения 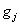 линейны относительно переменных
линейны относительно переменных 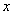 . Во вторых задачах целевая функция
. Во вторых задачах целевая функция 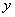 и (или) условия
и (или) условия 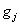 имеют разного рода нелинейности.
имеют разного рода нелинейности.
Графо-аналитический метод решения задач оптимизации
Этим методом вручную решаются простые задачи оптимизации. Математические модели в этих задачах не должны быть сложными, т.к. в противном случае требуется много времени для их решения. Для начала рассмотрим однопараметрическую однокритериальную задачу оптимизации.
Постановка задачи: Дан один критерий 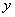 . Объект (процесс) описан уравнением (уравнениями), включающими один искомый параметр
. Объект (процесс) описан уравнением (уравнениями), включающими один искомый параметр 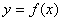 . Имеется система ограничений:
. Имеется система ограничений:
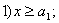
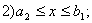
и т.д.
Необходимо найти оптимальное значение параметра 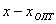 , обращающее целевую функцию
, обращающее целевую функцию 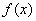 в максимум или минимум.
в максимум или минимум.
Задача решается в два этапа:
1. Построение области допустимых решений (ОДР).
2. Нахождение в пределах ОДР оптимального решения.
При построении ОДР на первом этапе рассматривается система ограничений. Все ограничения должны быть выполнены. Выполнение первого ограничения в приведенной выше постановке задачи оптимизации означает, что искомое значение параметра 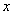 должно находиться правее
должно находиться правее 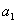 , причем,
, причем, 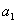 в разрешенный интервал входит (рис.5.1). Выполнение второго ограничения означает, что искомое значение параметра
в разрешенный интервал входит (рис.5.1). Выполнение второго ограничения означает, что искомое значение параметра 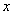 должно находиться в интервале (на отрезке)
должно находиться в интервале (на отрезке) 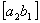 , следует иметь в виду, что границы интервала в интервал входят.
, следует иметь в виду, что границы интервала в интервал входят.
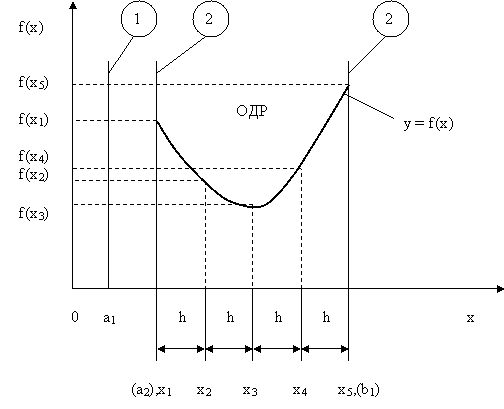
Рис.5.1. Графическая иллюстрация решения однопараметрической однокритериальной задачи оптимизации
Когда однопараметрическая однокритериальная задача оптимизации решается с применением графо-аналитического метода вручную, то на втором этапе применяют метод перебора. Суть его заключается в следующем. В пределах ОДР чере
| <== предыдущая лекция | | | следующая лекция ==> |
| Разложение функции отклика в степенной ряд, кодирование факторов | | | О системе моделей для исследования и управления |
Дата добавления: 2017-04-05; просмотров: 5583;










