Числовые функции на графе
Говорят, что на вершинах графа 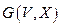 реализуется числовая функция, если каждой вершине
реализуется числовая функция, если каждой вершине 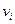 ставится в соответствие некоторое число
ставится в соответствие некоторое число 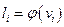 из некоторого множества L.
из некоторого множества L.
Значением маршрута через вершины 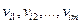 называется число
называется число 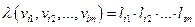 .
.
Минимальным (максимальным) маршрутомчерез вершины некоторого множества маршрутов Р называется маршрут с минимальным (максимальным) значением λ.
Говорят, что на ребрах графа 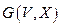 реализуется числовая функция, если каждому ребру
реализуется числовая функция, если каждому ребру 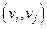 сопоставлено число
сопоставлено число 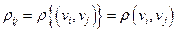 из некоторого множества М. Причем
из некоторого множества М. Причем 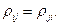
Значением маршрута через ребра, соединяющие вершины 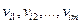 называется число
называется число 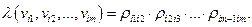
Минимальным (максимальным) маршрутом через ребра некоторого множества маршрутов Р называется маршрут с минимальным (максимальным) значением λ.
Деревья и леса
Деревом называется связный неориентированный граф 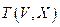 или
или 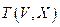 без цикла.
без цикла.
Лесом называется неориентированный граф, компонентами связности которого являются деревья.
Теорема (характеристические свойства дерева). Пусть граф 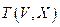 имеет n вершин. Тогда следующие утверждения равносильны:
имеет n вершин. Тогда следующие утверждения равносильны:
1) Т – дерево (определение)
2) Т не содержит циклов и имеет (n-1) ребер
3) Т – связен и имеет (n-1) ребер
4) Т – связен и каждое его ребро является мостом
5) Любые две вершины графа Т соединены ровно одной простой цепью
6) Т не содержит циклов, но, добавляя в него любое новое ребро, получим граф, содержащий ровно один цикл.
Остовным деревом называется подграф графа G, полученный стиранием ребер из циклов до удаления всех циклов, являющийся деревом.
Полным графом называется граф (без кратных ребер), в которых каждая пара вершин соединена ребром. Число рёбер полного графа равно 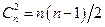 .
.
Теорема. Число остовных деревьев полного графа 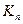 с n вершинами равно
с n вершинами равно 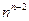 .
.
Следствие. Для произвольного простого графа с n вершинами число его остовных деревьев не превосходит числа 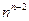 .
.
Дата добавления: 2017-04-05; просмотров: 1158;










