Средняя скорость вороха по соломотрясу и путь, пройденный за один оборот кривошипного вала

Средняя скорость перемещения равна

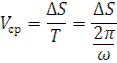
где ∆S – длина перемещения вороха вдоль клавиши за время одного оборота, М

Т – время одного оборота, С

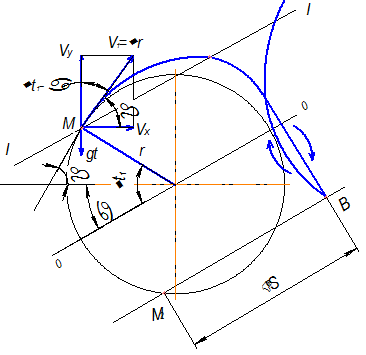
Частица вороха, отрываясь в точке «М» от вороха движется как тело, брошенное под углом 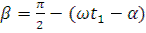к горизонту с начальной скоростью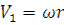

Значение 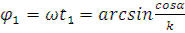найдено ранее

Скорости частицы по оси x и y будут:

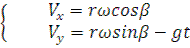
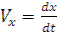
тогда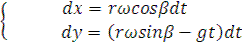

Параметрическое уравнение движения частицы вороха будут

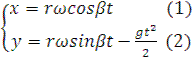это траектория движения частицы вороха (кривая- парабола)

Считая, что 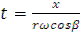(из 1го уравнения) подставим его в уравнение (2), получим 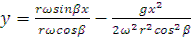или

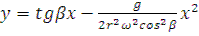
Задаваясь «x» можно получить «y» и построить траекторию.

Все эти уравнения справедливы, если начало координат перенести в точку «М».

За время полёта частицы вороха кривошип клавиши повернется на угол 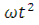от начального положения. Клавиша займет положение II, частица вороха встретится с рабочей поверхностью. Решая совместно уравнения параболы (полета вороха) и уравнение прямой (рабочей поверхности клавиши), можно найти координаты точки «В» встречи вороха и клавиши и угол поворота кривошипа 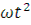, соответствующий положению клавиши в момент встречи.