Определение основных размеров триера и его производительности

При перемещении зернового материала в цилиндре триера он некоторым тонким слоем заполняет ячейки от одного конца к другому. При этом в ячейки попадают короткие примеси, которые в дальнейшем попадают в желоб.

Возможно два случая:

а) зерно расположилось между ячейками

б) зерно попало в ячейку

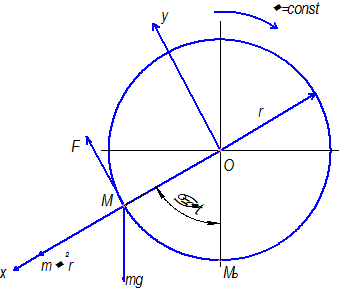
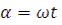(поворот)

m – масса зерна из положения M₀ в M

mg – сила тяжести

N – реакция

F – сила трения

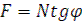
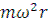- центробежная сила. Зерно будет в относительном покое, если сумма проекций сил на оси координат будет равна 0.

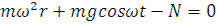
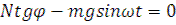
Подставив во 2ое уравнение N, найденное из 1го и обозначив показатель кинематического режима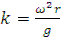

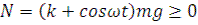
Условие относительного покоя зерна на поверхности вращающегося цилиндра.

разделим на g

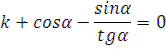
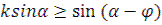
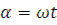
Так как в полученном выражении переменная t в правой части, то по истечении t 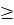t₁ зерно будет скользить по поверхности цилиндра 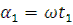, по которому намечается положение желоба (чтобы зерно не попало в него).

б) что же с зерном, попавшим в ячейку

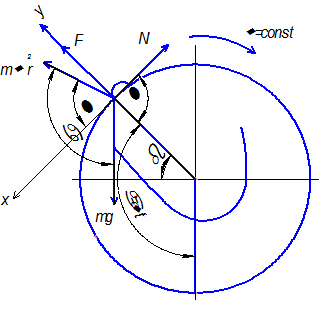
ось x – нормаль к поверхности ячейки, ось y – касательная к той же поверхности.

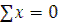
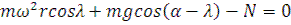
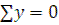
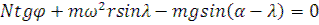
Определив из 1го уравнения N и подставив его во 2ое, а также обозначив соотношение 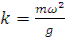и далее разделив на g получим условие относительного покоя зерна, попавшего в ячейку:

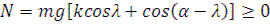
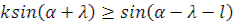
По мере увеличения угла 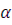правая часть приведенного уравнения будет возрастать и в определенный момент сравняется с левой частью выражения, что приведет к нарушению равновесия сил и зерно будет двигаться по ячейке.

Если обозначим , а угол поворота отсчитывать от горизонтального диаметра, то условие относительного покоя зерна будет:

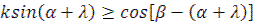
После выпадения зерна его движение определится реакцией N=0, то зерно будет перемещаться как тело брошенное со скоростью 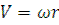под углом ;

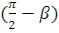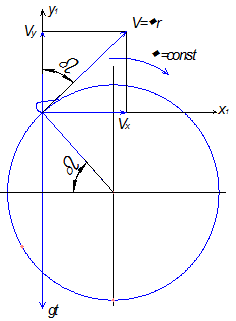
Начало подвижных координат м т.М. оси X₁ Y₁:

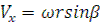
Тогда перемещение зерна определится координатами:

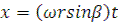
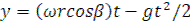
Это уравнение траектории движения зерна отсюда можно найти x_а, x_в и по ним судить о пожени желоба, чтобы он принял все выпавшие зерна. При 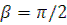условие (3) будет иметь вид:

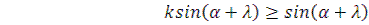, то есть выпадения

зерен не будет, следовательно выпадение зерен возможно при условии