Разновидности клина.
Рабочие органы почвообрабатывающих машин имеют форму клина. Такая особенность применения геометрического клина объясняется простотой его геометрической фигуры и разрушением почвы с использованием клина.
К примеру, всякую криволинейную поверхность можно разделить на ряд бесконечно малых плоских элементов, составляющих клин.
Ребра клина представляют собой ряд прямых линий – наикратчайшее расстояние между двумя точками на плоскости. Грани (плоскости) клина, соприкасающиеся с разрушаемым материалом называются рабочими. По числу рабочих граней клинья бывают одно-, двух-, и трехгранными.
В одногранном клине (рис. 3) рабочей гранью является плоскость АВ, установленная под углом α к горизонту. Другая плоскость АС – нерабочая и действия на почву не оказывает. Примером одногранных клиньев могут быть остро заточенные диски борон и лущильников. Однако в процессе износа дисков образуется опорная поверхность и одногранный клин превращается в двугранный, то есть одногранный клин ‑ это теоретическое понятие.
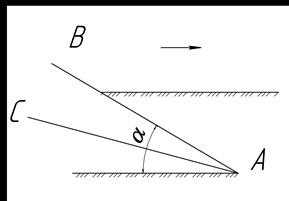
Рисунок 3 – Схема простого одногранного клина.
У двугранного клина (рис. 4) имеется две грани АВ и АС, которые установлены под углом α. В этом случае грань АВ является рабочей и деформирует почву, а грань АС является опорной плоскостью клина и лишь сминает ее. Двугранными клиньями могут служить зубья борон и рыхлительные лапы культиваторов.
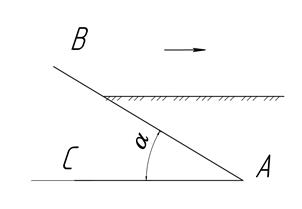
Рисунок 4 – Двугранный клин.
Трехгранный клин представляет собой тетраэдр АВСD (рис. 5). В общем виде он имеет три рабочие грани АВС, АВD и АСD, установленные под тремя углами α, β и γ. Рассмотрим значение каждого угла представив трехгранный клин как совокупность простых клиньев.
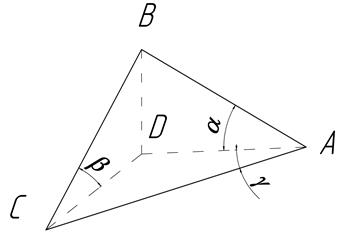
Рисунок 5 – Трехгранный клин.
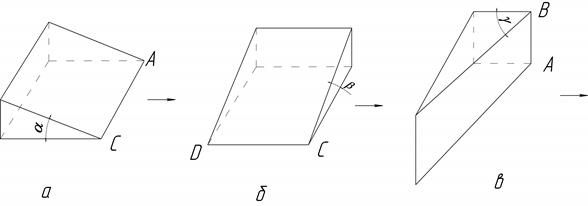
Рисунок 6 – Схема действия двугранных клиньев с углами:
а) крошения α; б) оборота β; в) сдвига γ.
У клина с углом крошения α (рис. 6а) ребро АС установлено перпендикулярно направлению движения, оно подрезает пласт почвы в горизонтальной плоскости, а рабочая грань поднимает его на себя. Пласт почвы изгибается и при недостаточной связности крошится. С увеличением угла α увеличивается изгиб и степень крошения пласта.
У клина с углом оборота β (рис. 6б) нижнее ребро СD совпадает с направлением движения, его рабочая плоскость наклоняет пласт в направлении, перпендикулярном движению, что способствует оборачиванию пласта. Увеличение угла β приводит к большему повороту пласта в поперечно-вертикальной плоскости.
У клина с углом сдвига γ (рис. 6в)ребро АВ перпендикулярно горизонтальной плоскости. Пласт почвы под воздействием рабочей плоскости этого клина сдвигается в сторону. Угол γ оказывает в горизонтальной плоскости такое же воздействие на пласт, как и угол α в вертикальной плоскости. Следовательно, совместное воздействие двух клиньев с углами α и γ способствует разрушению пласта в двух разных плоскостях.
Таким образом, в зависимости от положения рабочей грани простого клина по отношению к горизонтальной плоскости и направлению движения получаем различное действие клина на почву, в результате чего пласт подрезается, поворачивается или сдвигается в сторону.
Академик Горячкин В.П. показал, что существует такой клин, который один выполняет все перечисленные операции. Это косой трехгранный клин ABСD (рис. 7). Он снабжен одной рабочей гранью ABC и двумя опорными гранями ABD и ADC. Косой трехгранный клин характеризуется теми же углами α, β и γ, следовательно, один обладает технологическими свойствами всех трех простых клиньев в совокупности. Примером косых трехгранных клиньев служат корпуса лемешных плугов, а прямых трехгранных – стрельчатые лапы культиваторов.
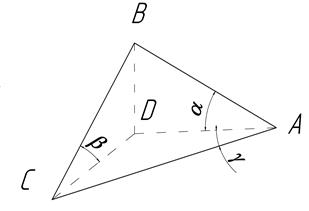
Рисунок 7 – Трехгранный клин.
2. Взаимосвязь углов в трехгранном клине. Характер деформации почвы зависит как от установки рабочей грани клина к горизонтальной и вертикальной плоскостям, так и от физико-механических свойств почвы.
Для изучения взаимосвязи углов рассмотрим трехгранный клин ABСD (рис. 7) и определим тангенсы его углов:
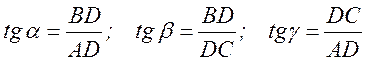
Умножив и разделив значение tgα на DС получим:
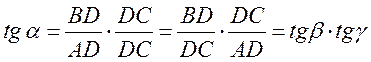
Этот простой вывод позволяет констатировать тот факт, что все углы в трехгранном клине взаимосвязаны и изменение одного из них ведет к изменению других. При проектировании поверхностей, особенно лемешно-отвальных, часто вместо угла β переходят к углу ε, наклона плоскости к горизонтальной поверхности (лемеха к дну борозды). Этот переход обоснован тем, что угол β может быть измерен и определен только при фактическом выполнении работ при вспашке. Для определения угла ε и его связи с другими углами проводят некоторые элементарные построения (рис. 8).
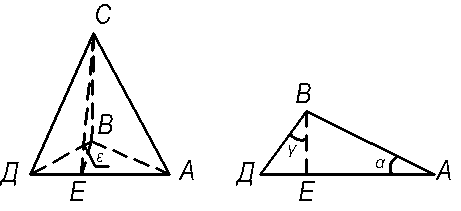
Рисунок 8 – Определение угла ε.
Определим тангенс угла ε:
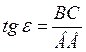
Учитывая, что 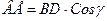 аналогично умножим и разделим значение tgα на BD Cosγ получим:
аналогично умножим и разделим значение tgα на BD Cosγ получим:
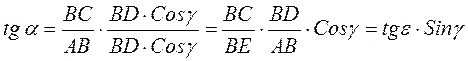
Дата добавления: 2017-03-12; просмотров: 4771;











