Динамический расчёт поршневого компрессора

Целью динамического расчёта является определение сил и моментов, действующих на детали кривошипно-шатунных групп, детали цилиндро-поршневых групп и корпусных элементов поршневого компрессора для последующего выполнения прочностных расчётов; уравновешивание действующих в компрессоре сил инерции; обеспечение требуемой неравномерности вращения коленчатого вала.

При выполнении этого раздела студент должен определить приведённые (эквивалентные) массы неуравновешенных вращающихся и возвратно-поступательно движущихся масс; выполнить уравновешивание сил инерции, возникающих при вращении неуравновешенных вращающихся конструктивных элементов и при неравномерном возвратно-поступательном движении вдоль оси ряда соответствующих элементов механизма движения и поршней; определить параметры маховика, построив для этого соответствующие диаграммы сил и моментов.

При определении приведённых масс учитывают отдельно соответствующие вращающиеся массы и массы, двигающиеся вдоль оси ряда, а массу шатуна, совершающего сложное вращательно-поступательное движение, делят на две части: m_ш1 = 0,3m_ш; m_ш2 = m_ш – m_ш1, сосредоточивая их на оси поршневого (крейцкопфного) пальца (m_ш1) и на оси мотылевой шейки коленчатого вала (m_ш2).

Приступая к динамическому расчёту, каждый ряд поршневого компрессора рассматривают отдельно, определяя суммарную поршневую силу и противодействующий момент в каждом из них, затем все моменты в рядах суммируют при построении суммарного противодействующего момента.

С учётом сказанного расчётную схему каждого ряда можно представить в следующем виде.

К поршневому пальцу приложена переменная суммарная поршневая сила P_пj; составляющие этой силы:

; ; ;

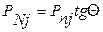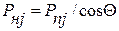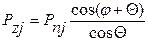передаются (P_Nj) на стенку цилиндра (или на направляющие крейцкопфа) или на направляющие крейцкопфа, сжимают (растягивают) шатун, нагружают мотылёвый и коренные подшипники у коленчатого вала. Центробежная сила инерции вращающихся масс, постоянная по величине Р_ин.врj = m_врjRω², приложенная к оси мотылевой шейки, растягивает кривошип и нагружает коренные подшипники коленчатого вала. К оси вращения коленчатого вала приложены момент движущих сил приводного двигателя М_{дв с} и противодействующий момент сил сопротивления М_с.сj = Р_mjR, приводящие к колебаниям частоты вращения n = ω/6,28 коленчатого вала при установившемся режиме работы.

Динамический расчет ведется для ряда последовательных положений кривошипа φ, отсчитываемых в направлении вращения, и перемещений поршня, отсчитываемых от ВМТ:

,

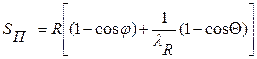где λ_R = R/L; Θ = arcsin(λ_Rsin φ).

Поршневая сила P_пj (кН) определяется алгебраической суммой сил, действующих вдоль оси ряда:

,

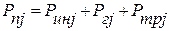где Р_инj – силы инерции поступательно движущихся масс; Р_zj – силы давления газа на поверхности поршня; P_mpj – суммарная сила трения в цилиндропоршневой группе, сальнике штока, направляющих крейцкопфа.

Результаты расчета составляющих суммарной силы заносят в таблицу и суммируют.

Необходимые для определения газовой силы значения мгновенных индикаторных давлений вычисляют аналитически в зависимости от угла поворота коленчатого вала (хода поршня).

Уравновешивание сил инерции однорядного ПК состоит в полном уравновешивании центробежных сил инерции вращающихся масс Р_ин._врj = m_врjRω² и частичном уравновешивании сил инерции масс, участвующих в возвратно-поступательном движении. Последние могут быть представлены в форме гармонического ряда:

,

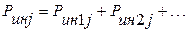где Р_ин1j = m_п.дjRω²соsφ; Р_ин2j = λ_Rm_п.дjRω²соs2φ, причем силы инерции второго и более высоких порядков обычно не уравновешивают, так как это требует введения в конструкцию машины дополнительных валов, вращающихся с частотой в два и более раз выше, чем номинальная частота вращения коленчатого вала. В многорядных ПК силы инерции первого Р_{ин 1j} и второго Р_{ин 2j} порядков стараются уравновесить силами инерции других рядов.

Рекомендуется следующий порядок расчета уравновешивания сил инерции:

1) в РПЗ вычерчивают схему ПК и на нее наносят действующие силы инерции;

2) по разработанным чертежам ПК определяют массы, приведенные к оси поршневого (крейцкопфного) и кривошипного пальцев:

; ,

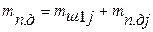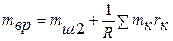где массы m_к определяют по чертежам или для унифицированных узлов по справочным данным.

В результате изменения в течение одного оборота коленчатого вала моментов сил сопротивления М_с.с = Р_ТR и движущихся сил М_дв.с возникают угловые ускорения.

По диаграмме суммарного противодействующего момента определяют приращения импульсов моментов сил ΔJ_m (кНмс), изображаемых величиной площадок ΔJ_m, заключенных между ординатами 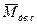и .

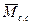Особенности динамики многорядных компрессоров. В многорядных ПК усилия, возникающие в каждом ряду, создают сложную систему сил. При сложении тангенциальных сил Р_тj (или противодействующих моментов) начало отсчета углов первого ряда φ = φ₁ совмещают с началом координат, а для диаграмм последующих рядов – перемещают вперед на угол Δφ_j = γ_j – φ_кj отставания ВМТ j-го ряда от ВМТ ряда I, где γ_j и φ_кj – углы развала цилиндров и опережения кривошипа j-го ряда по отношению к ряду I. На шатунные шейки коленчатого вала по-прежнему действуют силы P_тj и P_zj с равнодействующей 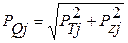, но реакции со стороны корпуса машины на коренные шейки коленчатого вала в многорядном ПК могут быть определены лишь методами, применяемыми для статически неопределимых систем.

Коренные шейки коленчатого вала передают крутящий момент М_кр = RΣР_Тj, величина которого является суммой крутящих моментов данного ряда и всех рядов, расположенных со стороны свободного конца коленчатого вала. Вычисление крутящих моментов рекомендуется вести в табличной форме, смещая начало отсчета углов φ на угол Δφ_j. Следует иметь в виду, что в многорядных ПК максимальное значение М_кр необязательно приходится на шейку, расположенную со стороны приводного двигателя.

Уравновешивание сил инерции возвратно-поступательно движущихся масс в многорядных ПК в ряде случаев может быть достигнуто выбором соответствующих схем ПК. Если это невозможно, то уравновешиванию подвергаются только силы инерции первого порядка с помощью установкипротивовесов аналогично однорядным ПК. При этом противовесы устанавливают на продолжении кривошипов таким образом, чтобы создаваемый ими момент был противоположным по знаку моменту от сил инерции первого порядка.

В приведённых ниже примерах рассмотрен динамический расчёт оппозитного и углового многорядного компрессоров, который позволит на конкретных примерах лучше разобраться с основными принципами, изложенными выше.

3.1. Примеры динамического расчёта поршневого компрессора