Пирамидальные и конические рупоры

Секторные электромагнитные рупоры обеспечивают су­жение диаграмм направленности только в одной плоскости, в которой происходит расширение рупора.

Для получения узких диаграмм направленности как в плоскости электрического, так и магнитного векторов поля рупоры делаются пирамидальными, т. е. расходящимися в обеих указанных плоскостях (рис. 30, а).

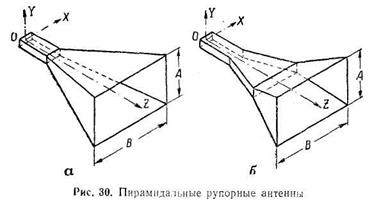
В отличие от секторного рупора в пирамидальных рупор­ных антеннах возникают уже не цилиндрические, а сфери­ческие волны, из-за чего коэффициент использования пло­щади их зева получается более низким, чем у секторных.

Структура поля в плоскости YOZ пирамидального рупора на рис. 30, а будет точно такой же, как в соответствующей плоскости Е – плоскостного рупора, а структура поля в сече­нии XOZ пирамидального рупора совпадает с таковой у Н – плоскостного рупора.

Диаграммы направленности пирамидальных рупоров в плоскостях XOZ и YOZ зависят лишь от размеров рупора и закона распределения поля в этих плоскостях и не зависят от аналогичных величин в соответствующих перпендикулярных плоскостях YOZ и XOZ. Последнее позволяет распространить выводы, сделанные в отношении секторных рупоров, и на пирамидальные рупоры. В частности, графики коэффициентов усиления, приведенные на рис, 28 и 29, могут быть применены для определения оптимальных размеров коэффициентов усиления пирамидальных рупоров.

Коэффициенты усиления пирамидальных рупорных антенн с помощью упомянутых графиков могут быть найдены как:

G_{пирамид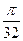} = G_e G_h ≈ 0, G_e G_h , (33)

где G_e — коэффициент усиления, определяемый по графику, приведенному на рис. 28, a G_h — по графику, приведенному на рис. 29.

Так, например, для пирамидального рупора, имеющего размеры А = 5l; В = 6lи l = 12l, на основе графиков имеем G_£ = 40, G_h = 48, а после подстановки в приведеннуювыше формулу G_{пирамид} = 0,1×40×48 = 192.

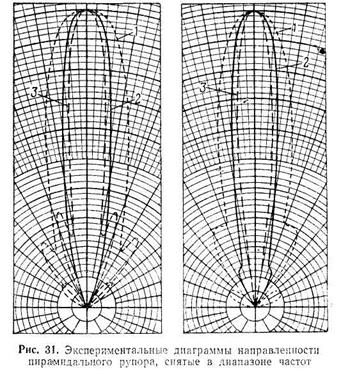
Чтобы дать представление о диапазонных свойствах пирамидальных рупорных антенн, на рис. 31 приведены диаграммы направленности, снятые экспериментально в плоскости Н (рис. 31, левый) и плоскости Е (рис. 31, правый) у рупора, имеющего размеры А = 4,5l, В=5l и l = 7l (см. рис. 30, а). Кривые 2 на рис. 31 соответствуют расчетной длине волны l₂ = l₀, а кривые 1 и 3 сняты при значительных отклонениях рабочей волны от расчетной: l₁=0,6l₀ и l₃= 1,7l₀.

Кривые, приведенные на рис. 31, показывают, что диаграммы в плоскостях Е и Н отличаются лишь в деталях и мало меняются при изменениях рабочей частоты. Эта особенность рупорных антенн оказывается особенно важной тех случаях, когда возникает необходимость применения широкодиапазонных антенн.

На практике, помимо рассмотренных, часто применяется своеобразная разновидность пирамидальных рупоров, (см. рис. 30,б). У рупоров этого типа начало расширения узкой и широкой сторон волновода находится не в одном общем поперечном сечении, а разнесено по длине рупора.

Делается это для улучшения согласования рупора с волноводом.

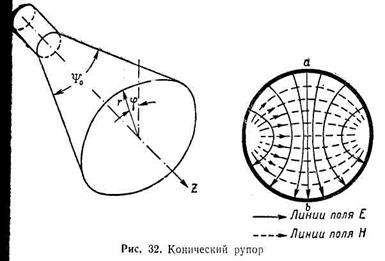
На рис. 32 показан конический рупор, образованный в результате плавного увеличения поперечного сечения круг­лого волновода. Справа на этом же рисунке показана струк­тура поля в произвольном сечении рупора, получающаяся при возбуждении в круглом волноводе основной магнитной волны типа H₁.

Рупоры с прямоугольным поперечным сечением приме­няются наиболее часто, как более простые в изготовлении. Конические антенны применяются исключительно редко из-за неустойчивости положения поляризации распространяю­щихся в них волн. Так, например, придание сечению конуса даже небольшой эллиптичности может вызвать поворот всей картины поля, показанной на рис. 32, на некоторый угол, определяемый положением осей эллипса поперечного сечения рупора (линия ab будет совпадать с малой осью эллипса).

Вообще в качестве самостоятельных рупорные антенны применяются редко. Чаще всего они служат облучателями зеркал и линз или составным элементом так называемых рупорно-линзовых антенн, рассматриваемых дальше.