Поле линейной системы идентичных излучателей.

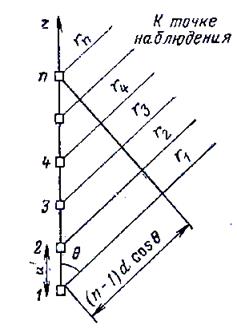
Рис.87. Линейная система идентичных излучателей.

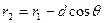
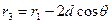
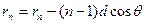
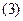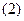Подставляя в получим

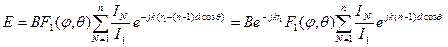
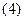
Абсолютное значение 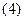определяет собой диаграмму направленности линейной тсистемы идентичных излучателей.

Множитель

-

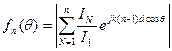- является множителем решетки. Он не зависит от 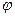. Это обстоятельство позволяет применять правило перемножения диаграммы направленности для любой плоскости 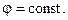в пространстве, используя один и тот же множитель системы.

Частный случай 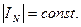, фазы итающих токов изменяются по линейному закону.

,

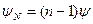где 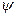- угол сдвига фаз между токами соседних излучателей; т.е. предполагается, что

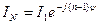
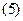
Подставляя 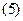в 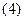и учитывая, что амплитуды токов приняты равными 1, получаем

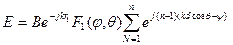
В выражение 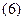входит сумма 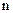членов геометрической прогрессии , .

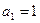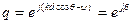Сумма 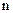членов геометрической прогрессии

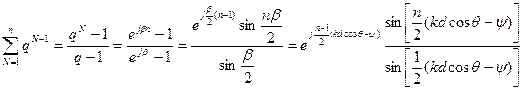
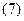
Подставляя выражение 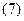в выражение 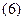, получим

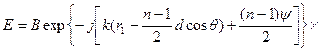
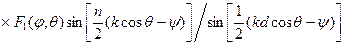
Выражение является очень важным в теории антенн. Множитель 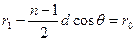в показателе есть расстояние от середины антенной системы до точки наблюдения, а 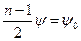определяет фазовый угол тока, соответствующего той же средней точке антенны. При указанных обозначениях выражение 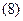можно переписать:

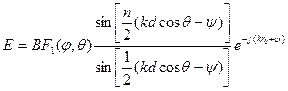
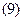
Модуль выражения 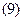определяет собой амплитудную характеристику направленности рассматриваемой системы направленных излучателей. Фазовый множитель выражения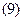

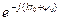
определяет фазовую характеристику системы, а следовательно, форму ее волновой поверхности (поверхности равных фаз). При сферической форме волновой поверхности ее центр называется фазовым центром антенной системы.

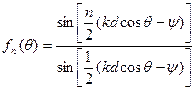
Это выражение определяет собой диаграмму направленности линейной системы из 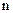ненаправленных излучателей и является так называемым множителем решетки.

-

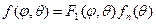- диаграмма направленности из 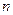- ненаправленных излучателей.

Выражение 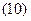определяет ненормированную диаграмму направленности системы из 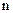ненаправленных излучателей, так как его максимальное значение отличается от единицы и равно 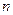при 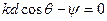. Действительно, при этом выражение 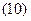превращается в неопределенность вида .

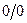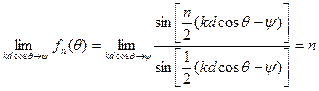
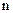определяет максимально возможное значение выражения 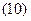. Поэтому нормированное значение этого выражения будет

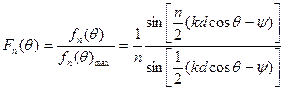
Рассмотрим несколько случаев.