Температурный напор

Рабочий процесс рекуперативного теплообменника описывается двумя уравнениями: уравнением теплового баланса (баланса энергии) и уравнением теплопередачи. Так как скорости движения теплоносителей в каналах теплообменника обычно малы, то в тепловом балансе их изменением можно пренебречь. Тогда для газообразных теплоносителей в процессе их прохождения через теплообменник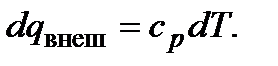

При отсутствии потерь теплоты в окружающую среду тепловой баланс теплообменника сводится к равенству количества теплоты, отбираемой от горячего теплоносителя, и количества теплоты, отдаваемой холодному теплоносителю, т.е. Q 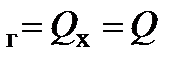, Для теплообменника с газообразными теплоносителями это приводит к равенству:

Q = G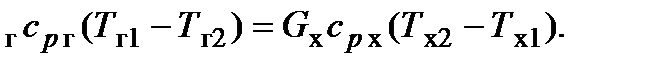

Здесь: 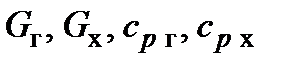― массовые расходы и теплоёмкости горячего и холодного теплоносителей, а 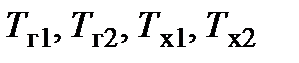― температуры горячего и холодного теплоносителей на входе и выходе теплообменника.

Если какой-либо из теплоносителей не газообразный, то далее его теплоемкость условно будем также обозначать символом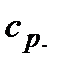

Если в процессе нагрева или охлаждения теплоноситель изменяет свое агрегатное состояние, то надо учесть дополнительно его теплоту испарения. Но в дальнейшем такие процессы будут полагаться отсутствующими.

Обозначим через 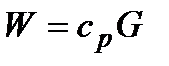полную теплоёмкость массы теплоносителя, проходящей через теплообменник в единицу времени, которую принято называть водяным эквивалентом.¹⁾С учётом такого обозначения уравнение (14.1) примет вид:

Q = ,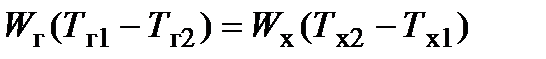

откуда

.

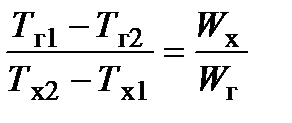Отсюда следует, что изменение температуры теплоносителей в теплообменнике обратно пропорционально их водяным эквивалентам. При равенстве водяных эквивалентов изменение температуры теплоносителей одинаково.

Рассмотрим характер изменения температур горячего 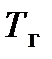и холодного 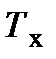теплоносителей (рис. 14.4) по ходу их движения от входа в теплообменник (F = 0) до выхода из него (F = F 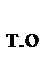), условно откладывая по оси абсцисс долю общей площади теплообмена, омываемую каждым теплоносителем с начала поступления его в теплообменник. На рис. 14.4, а показано изменение 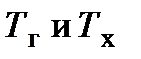в прямоточном, а на рис.14.4, б ― в противоточном теплообменных аппаратах при различных соотношениях водяных эквивалентов. Здесь же видно, как изменяется величина температурного напора в этих теплообменниках ( 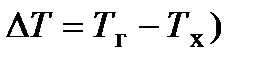от входа к выходу.

В прямоточном теплообменнике (см. рис. 14.4, а) температурный напор на входе ( 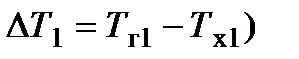максимальный. По мере движения теплоносителей вдоль каналов температура горячего теплоносителя уменьшается, а холодного увеличивается. Поэтому тем-

1). Этот термин был введен (и сохранился с тех пор) в то время, когда в старой системе единиц теплоёмкость воды (удельная) была равна 1 ккал/(кгּК), где 1 ккал = 4,1868 кДж.

Рис. 5.4. Характер изменения температуры теплоносителей в различных теплообменниках

пературный напор ( 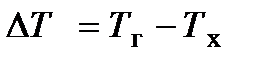) от входа к выходу уменьшается и на выходе из теплообменника его значение 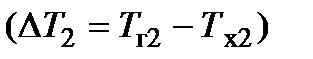минимальное.

В противоточном теплообменнике (см. рис. 14.4, б), если вести отсчет F по направлению движения горячего теплоносителя, температурный напор на входе меньше, а на выходе больше, чем в прямоточном теплообменнике (при условии, что теплоносители в них имеют одни и те же начальные температуры).

На входе температурный напор меньше потому, что при встречном движении холодный теплоноситель к этой стороне теплообменника подходит подогретым. На выходе температурный напор больше, так как холодный теплоноситель имеет здесь еще начальную температуру.

Температура холодного теплоносителя на выходе из противоточного теплообменника может быть даже больше конечной температуры горячего теплоносителя.

При равных значениях водяных эквивалентов температурный напор в противоточном теплообменнике остается постоянным от входа до выхода.

Таким образом, температурный напор в противоточном теплообменнике изменяется в меньшей степени, чем в прямоточном.

Для случая, когда площадь рабочей поверхности теплообменника с горячей и холодной сторон одинакова, а температурный напор на рабочей поверхности переменный, уравнение теплопередачи имеет вид:

Q = ,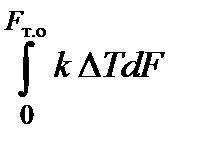

где k — коэффициент теплопередачи через рабочую поверхность теплообменника.

В расчётах обычно используется величина среднего температурного напора, равного:

.

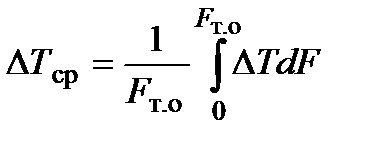Принимая коэффициент теплопередачи постоянным на всей рабочей поверхности теплообменника (k = const), получим

Q = k .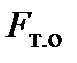

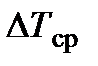Выведем формулу для определения среднего температурного напора. Рассмотрим наиболее простой случай ― прямоточную схему теплообменника.

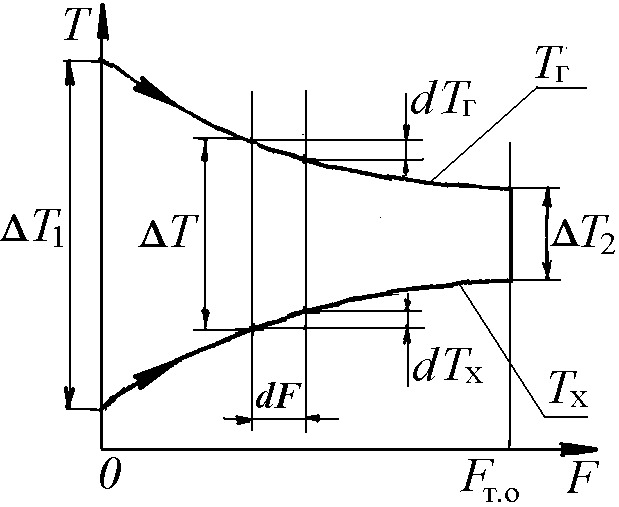
Рис. 5.5. Характер изменения температуры в прямоточном теплообменнике

Количество теплоты, передаваемое в единицу времени через элементарный участок рабочей поверхности dF (рис. 14.5), составляет

dQ = k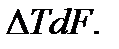

При этом температуры горячего и холодного теплоносителей на участке dF изменяются следующим образом:

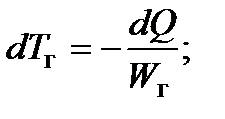
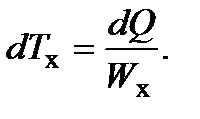
Уменьшение температурного напора на участке dF равно:

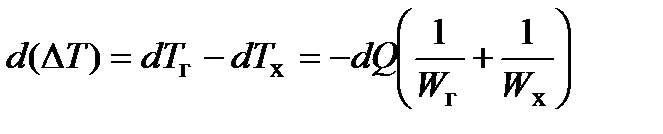
или 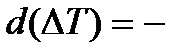mdQ, где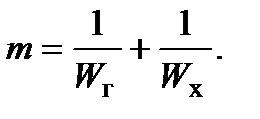

Подставив в (14.6) dQ из формулы (14.5) и разделяя переменные, получим

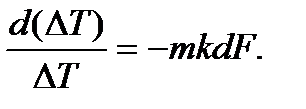
Проинтегрируем это равенство, считая k и m постоянными,

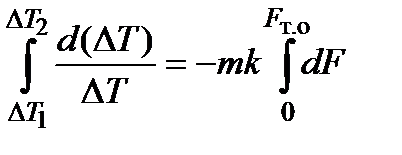
и получим

ln .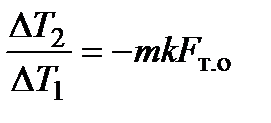

Определим зависимость параметра m от параметров теплообменника, используя формулы (14.2) и (14.7),

.

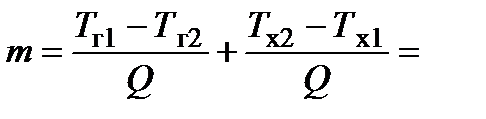
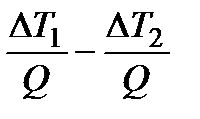А из формулы (14.4) найдем kF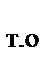

kF = .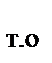

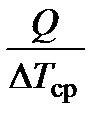Тогда, подставляя эти выражения в формулу (14.8), после несложных преобразований получим

.

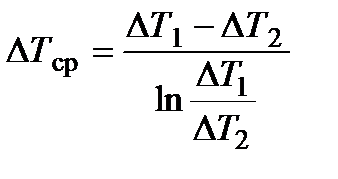Определённое по формуле (14.9) значение среднего температурного напора часто называют среднелогарифмическим.

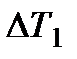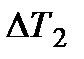Формула (14.9) применима и для противоточной схемы теплообменника. Но в этом случае значения и (см. рис. 14.4, б) определяются так:

; .

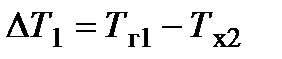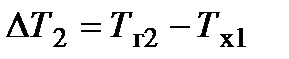Если разница между 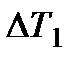и 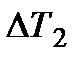невелика, то значение 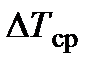может быть приближенно определено как

.

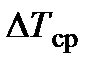
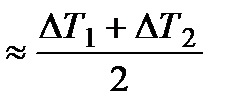Аналитическое определение среднего температурного напора для теплообменников с перекрёстным током и другими сложными схемами движения теплоносителей ( 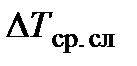) оказывается более трудной задачей. В этих случаях средний температурный напор определяется по формуле

,

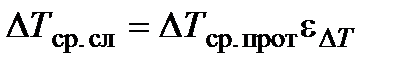где 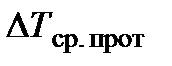- средний температурный напор, определяемый по формуле (14.9) для противоточной схемы; 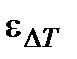- поправочный коэффициент, значения которого рассчитаны для теплообменников с различными схемами движения теплоносителей и приводятся в справочной литературе.

Следует отметить, что во всех случаях 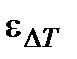< 1.

Сравнение средних температурных напоров при различных схемах движения теплоносителей показывает, что при одинаковых значениях соответствующих температур теплоносителей на входе теплообменного аппарата в противоточном теплообменнике средний температурный напор получается наибольшим, а в прямоточном - наименьшим. При других схемах движения теплоносителей он имеет промежуточные значения. Поэтому во многих случаях при выборе схемы теплообменника предпочтение отдаётся противоточному теплообменнику. Но вместе с тем определённое значение имеют конструктивные и эксплуатационные факторы (компоновка, удобство монтажа и др.), которые в конечном итоге могут определять выбор схемы движения теплоносителей.

В теории теплообменных аппаратов используется понятие степени регенерации, равной отношению действительного теплового потока в теплообменнике к его максимально возможному значению при данных расходах теплоносителей и данных их температурах на входе в теплообменник. Максимально возможное значение теплового потока очевидно равно

Q .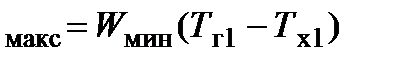

В этой формуле 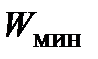- меньший из водяных эквивалентов теплоносителей, используемых в теплообменнике. Тогда

.

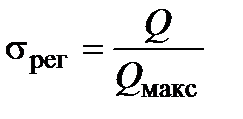Чем больше значение 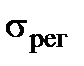, тем более эффективно используется теплообменник для передачи теплоты. Во всех реальных теплообменниках 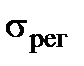< 1. Следует отметить, что при равных значениях 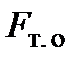и коэффициента теплопередачи k степень регенерации в противоточных теплообменниках, как правило, выше, чем в прямоточных. Но если один из водяных эквивалентов много больше другого, т.е. 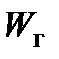>> 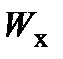или 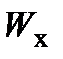>> 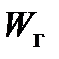, то степень регенерации у прямоточного и противоточного теплообменников при прочих равных условиях оказывается практически одинакова (так как в этом случае температура .одного из теплоносителей в процессе его прохождения через теплообменник почти не изменяется).