Проектирование оптимальной системы поверхностного водоотвода
Для моделирования и расчета гидрологических и гидравлических параметров ливневого стока применяются более точные физико-математические зависимости, описывающие нестационарный процесс формирования и отекания ливневых вод по склонам водосбора (см. уравнения 31.1).
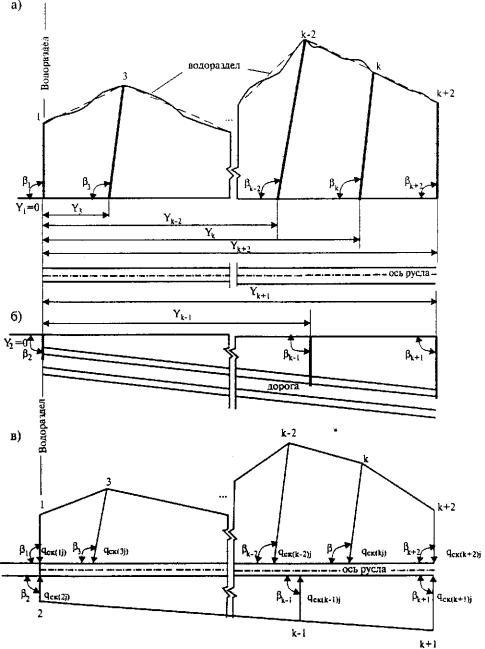
Рис. 31.13. Схематизация водосборного бассейна:
а - схема склона бассейна с нагорной стороны; б - то же со стороны дороги; в - эпюра боковых приточностей
Схематизацию водосбора выполняют заменой криволинейного очертания водораздела кусочно-ломаными отрезками, практически не нарушая общую конфигурацию бассейна (рис. 31.13). Искусственные русла водоотводных сооружений (кювет, канава, быстроток, перепад и т.д.) принимают в качестве главного лога. Водосборный бассейн может быть расположен как с одной стороны отводящего русла (как у нагорной канавы), так и с обеих сторон (как у боковых кюветов).
Чтобы наиболее точно определить ливневый склоновой расход (что является особо важным для очень маленьких водосборов с гладкой поверхностью) по кинематическим уравнениям (31.1) элементарный расход на полосе склона шириной 1 м представляется в виде:
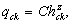 где
где
hck - глубина склонового потока, м (рис. 31.14, г);
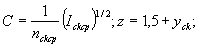
yck - показатель степени, зависящий от шероховатости поверхности;
Ickcp, nckcp - осредненные величины уклона и коэффициента шероховатости рассматриваемой полосы склона.
Поверхность склона вдоль каждой выделенной расчетной полосы может иметь множество участков длиной Lck(ki) с различными уклонами Ick(ki) и шероховатостями (см. рис. 31.14, б).
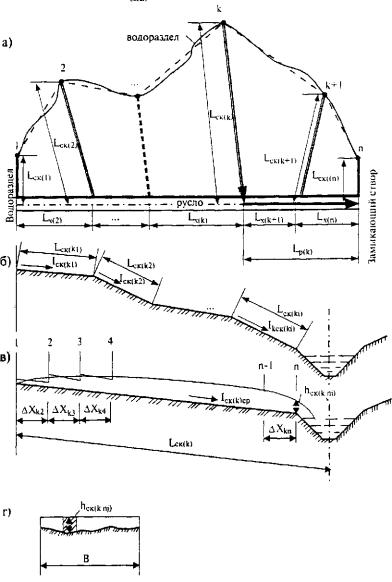
Рис. 31.14. Схема к расчету склонового стока:
а - водосборный бассейн; б - профиль естественного склона вдоль оси расчетной полосы; в - схематизация склона и кривая свободной поверхности стока; г - поперечный разрез склона шириной В
Во избежание сложности и трудоемкости расчета для отдельных i-х участков рассматриваемой k-й полосы склона ее схематизируют в виде односкатной поверхности со своими осредненными величинами уклона Ick(ki)cp и коэффициента шероховатости nckcp (см. рис. 31.14, в).
С учетом сказанного система уравнений (31.1) в конечных разностях для k-й полосы склона представляется в виде:
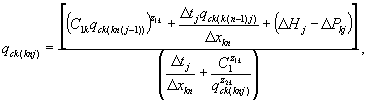 где (31.28)
где (31.28)
qck(knj) - погонный расход в n-м расчетном участке k-й полосы склона при j-м интервале времени, м2/с;
qck(kn(j-1)) - то же при (j-1)-м интервале времени;
qck(k(n-1)j) - то же в (п-1)-м участке полосы при j-м интервале времени;
Dtj - расчетный j-й интервал времени, с;
Dxkn - расчетный n-й интервал длины k-й полосы, м;
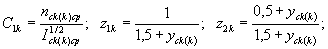
псk(k)cp, Iсk(k)cp - осредненные значения коэффициента шероховатости и уклона k-й полосы склона;
yсk(k) - показатель степени (с некоторым упрощением 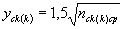 );
);
DНj, DРkj - приращения слоев осадков и потерь за j-й интервал времени, определяемые по следующим формулам:
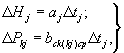 где
где
аj - расчетная интенсивность ливня при j-м интервале времени, мм/мин;
bсk(kj)cp - осредненная скорость потерь для k-й полосы склона при j-м интервале времени, м/с.
Решая уравнение (31.28), получают эпюры боковой приточности по длине русла для всех j-x интервалов времени с учетом углов примыкания векторов притоков bк к направлению оси русла (см. рис 31.13).
Как установлено, при решении кинематических уравнений (31.28) точность расчета существенно зависит от интервалов времени Dt и длины Dx. Поэтому для каждой расчетной полосы водосбора определяют оптимальные расчетные интервалы времени Dton и длины Dx(kn)on по формулам:
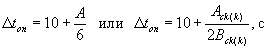 (Dton принимают меньшее из двух)
(Dton принимают меньшее из двух)
Dx(kn)on = 5 + Сck(k)(Аck(k) - Bck(k)Dton), м, где
А - параметр, определяемый по табл. 31.10 в зависимости от уклона Iр и коэффициента шероховатости поверхности nр русла;
Таблица 31.10.
Параметры А и В
| Уклон русла Iр | Параметр А при nр | Параметр В при nр | ||||||||||
| 0,012 | 0,015 | 0,018 | 0,021 | 0,024 | 0,030 | 0,012 | 0,015 | 0,018 | 0,021 | 0,024 | 0,030 | |
| 0,005 | 84,53 | 119,9 | 148,2 | 119,5 | 63,99 | 61,20 | 0,153 | 0,267 | 0,346 | 0,228 | 0,044 | 0,022 |
| 0,020 | 35,40 | 37,40 | 37,70 | 40,39 | 45,87 | 71,31 | 0,014 | 0,020 | 0,026 | 0,038 | 0,063 | 0,166 |
| 0,040 | 33,54 | 34,39 | 36,60 | 34,44 | 34,72 | 37,40 | 0,006 | 0,009 | 0,013 | 0,013 | 0,020 | 0,034 |
| 0,080 | 34,28 | 33,71 | 31,90 | 33,94 | 32,48 | 33,60 | 0,005 | 0,005 | 0.007 | 0,007 | 0,009 | 0,013 |
Аck(k) , Bck(k), Сck(k) - параметры расчетной k-й полосы, зависящие от уклона склона и коэффициента его шероховатости, определяемые по формулам:
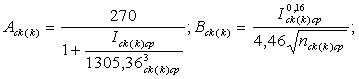
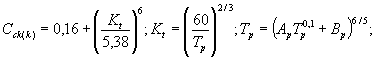
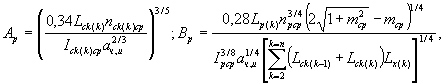 где
где
Tp - расчетная продолжительность наиболее опасного ливня (т.е. время добегания по комбинированной траектории, как правило, от наиболее удаленной точки водораздела склона до замыкающего створа русла);
Lck(k) - длина рассматриваемой k-й полосы склона, м;
nсk(k)cp, Iсk(k)cp - осредненные величины коэффициента шероховатости и уклона k-й полосы склона;
ач,и- избыточная интенсивность ливня часовой продолжительности, мм/мин;
прср, mcp, Ipcp - осредненные величины коэффициентов шероховатости, заложения откосов и уклона русла;
Lx(k) - расстояние между устьями (k-1)-й и k-й полос склона, м;
Lp(k) - расстояние от конца k-й полосы склона до замыкающего створа русла, как часть траектории для определения времени добегания(см. рис. 31.14, а), м.
Для расчета ливневого склонового стока канд. техн. наук С.П. Паудяль разработаны алгоритм и программа, которая применима как в практических, так и в исследовательских целях.
Среди сооружений поверхностного водоотвода наиболее распространены искусственные призматические русла треугольной, прямоугольной и трапецеидальной форм поперечного сечения (рис. 31.15).
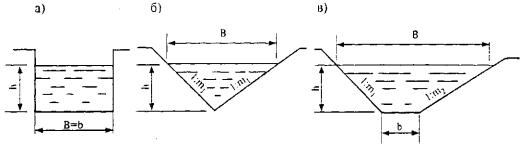
Рис. 31.15. Схемы призматических русел:
а - прямоугольное русло; б - треугольное русло; в - трапецеидальное русло
Применительно к открытым призматическим руслам с непрерывной боковой приточностью система уравнений (31.3), описывающая неустановившееся движение ливневых вод, представляется в следующем виде:
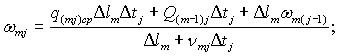 (31.29)
(31.29)
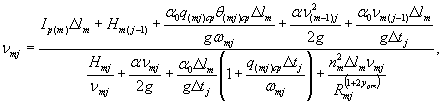 где (31.30)
где (31.30)
Ip(m) - уклон m-го участка русла, ‰;
Dlm - m-й расчетный интервал длины русла, м;
q(mj)cp - средняя погонная боковая приточность в m-м участке русла при j-м интервале времени, м2/с;
q(mj)cp - средняя проекция скорости боковой приточности на направлении скорости потока в m-м участке русла при j-м интервале времени, м/с;
Dtj - расчетный j-й интервал времени;
Нmj, wmj, vmj, Rmj - соответственно глубина (м), площадь живого сечения (м2), средняя скорость (м/с) и гидравлический радиус (м) в m-м створе русла при j-м интервале времени;
пт - коэффициент шероховатости m-го участка русла;
ут - показатель степени для этого же участка в формуле Н. Н. Павловского.
Среднюю боковую приточность для m-го участка русла при j-м интервале времени q(mj)cp определяют по формулам:
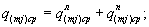
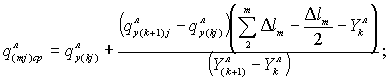
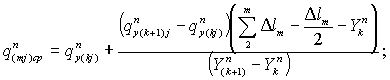 где
где
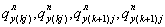 - погонные боковые приточности в устьях k-x и (k+1)-x полос левого и правого склонов в j-м интервале времени, м/с;
- погонные боковые приточности в устьях k-x и (k+1)-x полос левого и правого склонов в j-м интервале времени, м/с;
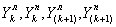 - соответственно расстояния от водораздела русла до устьев k-x и (k+1)-х полос, расположенных слева и справа от оси русла (см. рис. 31.13).
- соответственно расстояния от водораздела русла до устьев k-x и (k+1)-х полос, расположенных слева и справа от оси русла (см. рис. 31.13).
По аналогичным формулам определяют и средние проекции скоростей боковых приточностей 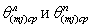 для m-го участка русла (с учетом проекции скоростей боковых приточностей
для m-го участка русла (с учетом проекции скоростей боковых приточностей 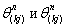 в устье каждой k-й полосы склона) при j-м интервале времени:
в устье каждой k-й полосы склона) при j-м интервале времени:
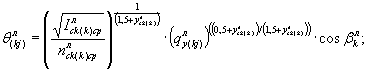
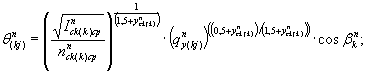
где 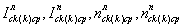 - соответственно осредненные уклоны и коэффициенты шероховатости k-x полос левого и правого склонов;
- соответственно осредненные уклоны и коэффициенты шероховатости k-x полос левого и правого склонов;
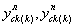 - показатели степени для тех же полос;
- показатели степени для тех же полос;
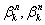 - углы подхода направлений боковых приточностей k-x полос левого и правого склонов к оси русла (в случае затруднений в определении их можно принять равными 90°).
- углы подхода направлений боковых приточностей k-x полос левого и правого склонов к оси русла (в случае затруднений в определении их можно принять равными 90°).
Алгоритм расчета нагорных, водоотводных и боковых канав с прямым постоянным уклоном следующий:
1. Делят каждый рассматриваемый односкатный участок водоотводного русла по длине на оптимальное количество расчетных интервалов Dl(m)оп
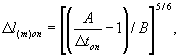 где
где
А и В - параметры, определяемые по табл. 31.10;
Dtоп - оптимальный расчетный интервал времени, с.
2. Определяют и вводят другие необходимые исходные данные: коэффициенты Кориолиса и Буссенеска, пределы точности расчета скорости Dv и глубины потока DН в русле, коэффициенты заложения откосов и шероховатости, уклон дна и ширину по дну русла и др.
3. Задают величины скорости и расхода в начальном створе русла (как правило, они равны нулю) для всех расчетных интервалов времени Dtj, а также глубины, скорости и расходы для первого интервала времени Dt1, по всем расчетным интервалам длины Dlm (как правило, они также равны нулю).
4. Определяют величины 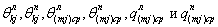 по соответствующим формулам.
по соответствующим формулам.
5. Далее по уравнениям (31.29) и (31.30) определяют величины vmj, Hmj, Qmj и другие необходимые характеристики.
6. Завершают расчет, последовательно решая указанные уравнения по каждой паре створов сверху вниз для всех расчетных интервалов времени.
Уравнения (31.29) и (31.30) описывают плавноизменяющееся течение как в бурном, так и в спокойном состоянии. В местах перехода от бурного к спокойному состоянию (гидравлический прыжок) или наоборот (водопад) поток подвергается разрыву (рис. 31.16). В таких местах эти уравнения неприемлемы. Поэтому для расчета входных и выходных участков сопрягающих сооружений (быстротоков, перепадов и т.д.) применяются известные зависимости прикладной гидравлики.
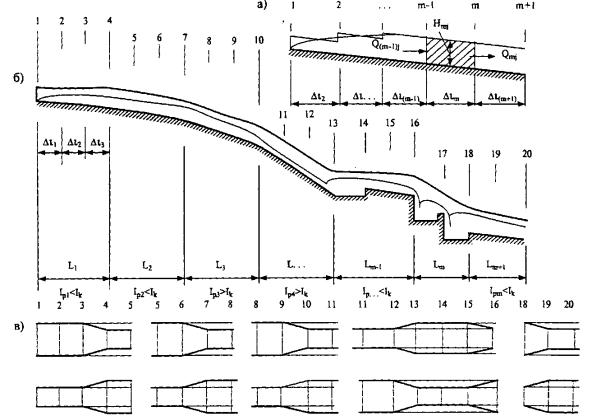
Рис. 31.16. Схемы к гидравлическому расчету и стыковки конструктивных участков русел:
а - кривая свободной поверхности в призматическом русле; б - кривая свободной поверхности в системе водоотводных сооружений; в - схемы стыковки конструктивных участков различными формами поперечных сечений; Dlm - расчетные интервалы длины; Iр - уклоны дна русла; Ik - критический уклон
При гидравлических расчетах быстротока учитывается влияние аэрации потока. Например, для m-го участка русла при j-м интервале времени по числу Фруда определяют состояние потока в конце подводящего русла, а затем соответствующие гидравлические характеристики по известным зависимостям. Число Фруда FR(mj) коэффициент аэрации Ae(mj) и критическую скорость потока vkp(mj) определяют по формулам:
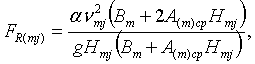
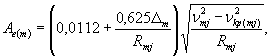
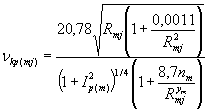 где
где
Hmj, vmj, Rmj - соответственно глубина и скорость нормального потока и гидравлический радиус в m-м створе при j-м интервале времени, м, м/с;
Bm, A(m)cp, пm, Ip(m), Dm - соответственно ширина по низу, средний коэффициент заложения откосов, коэффициент шероховатости, уклон и абсолютная шероховатость m-го участка русла;
Расчет водоската быстротока аналогичен расчету канав (кюветов). Сравнивая уклон отводящего русла с критическим, осуществляют его сопряжение по общей методике расчета нижнего бьефа.
На участках, где рассматриваются перепады, определяют необходимые максимальные характеристики потока в конечном створе подводящего русла (над первой стенкой падения) по приведенной методике гидравлического расчета, а для расчета их тела и выходных участков применяются известные зависимости гидравлики. Рассматриваются перепады как колодезного, так и бесколодезного типа (хотя последний рассматривают исключительно редко из-за его неоправданно длинных ступеней).
Итогом расчета гидравлических характеристик является получение максимальных значений Vmaх, wmaх и Нmaх во всех расчетных створах, а также характеристик потока в замыкающем створе русла во всех интервалах времени.
С.П. Паудяль разработаны методика, алгоритм и программа «HYDRAN» для расчета гидравлических характеристик неустановившегося течения ливневых вод по сооружениям системы поверхностного дорожного водоотвода (см. рис. 31.16, б) в неразрывной связи с водосборным бассейном.
Проектирование оптимальных конструкций системы поверхностного водоотвода является задачей оптимизации с несколькими зависимыми и независимыми переменными при наличии комплекса технических ограничений. В первую группу переменных входят параметры поперечного сечения сооружений при фиксированных значениях второй, а во вторую группу входят стоимостные и прочие характеристики рассматриваемых типов укреплений относительно каждого конструктивного участка.
Для рассматриваемых сооружений в качестве функций цели обычно принимают строительную стоимость одного погонного метра длины тела проектируемого сооружения
СCT = WгрCгр + WyкCyк + ВзСз ® min, где
Wгр, Wyк - объемы земляных работ и укреплений на 1 п.м. длины сооружения;
Cгр, Cyк - суммарные стоимости единицы объема разработки грунта и укрепления;
Вз, Сз - средняя ширина полосы отвода земли на рассматриваемом участке и стоимость 1 м2 ее площади.
Последовательность оптимизации формы поперечного сечения водоотводных сооружений методом покоординатного спуска при фиксированном типе укрепления и график изменения направления функции цели представлены на рис. 31.17.
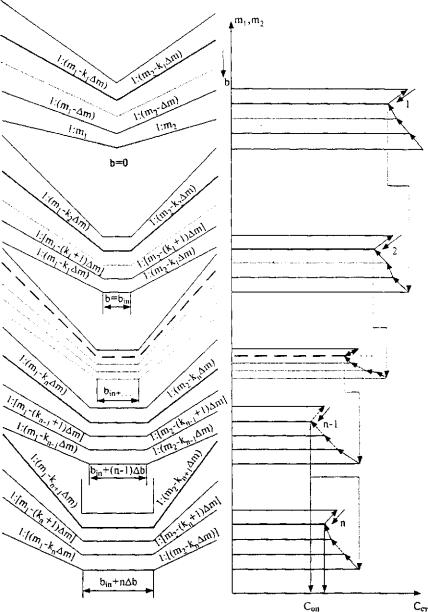
Рис. 31.17. Последовательность оптимизации формы поперечного сечения искусственного призматического русла и изменение направления функции цели Сст
Основными ограничениями при проектировании канав и кюветов треугольной формы (по конкретному типу укрепления) являются коэффициенты заложения откосов
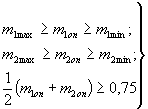 где
где
m1maх, m2maх, m1min, m2min, m1оn, m2оn - соответственно максимальные, минимальные и оптимальные коэффициенты заложения откосов.
Для прямоугольной и трапецеидальной форм поперечного сечения канав, кюветов и быстротоков область поиска оптимального решения с учетом технических ограничений по откосам находится в пределах
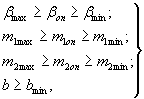 где
где
b - текущая ширина дна русла, изменяемая с заданным шагом Db, м;
bmin - минимально допустимая ширина дна русла, м;
bmaх, bmin - максимальная и минимальная относительные ширины, определяемые по 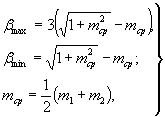 где
где
т1, т2 - текущие коэффициенты заложения откосов, меняемых с заданным шагом Dт.
При сопряжении бьефов перепадами рассматривают трапецеидальную и прямоугольную формы поперечного сечения как для одноступенчатого, так и для многоступенчатого перепадов колодезного и бесколодезного типа. При этом, если последний расчетный участок подводящего русла (перед перепадом) имеет в качестве оптимального трапецеидальное сечение, то форму сечения входной части над первой стенкой рассматриваемого перепада принимают с теми же параметрами, что и у конца подводящего русла, а если последний расчетный участок подводящего русла прямоугольный, то трапецеидальную форму вообще не рассматривают. Кроме этого, конструкции перепадов оптимизируют и по высоте стенки падения Р. Оптимальная высота Роп находится в пределах
Рmaх ³ Роп > Рmin.
Для окончательного выбора типа водоотводного сооружения на конкретном конструктивном участке после подбора оптимального поперечного сечения по одному типу укрепления рассматривают следующий тип укрепления по заданному типу сооружения, а затем сравнивают конечные строительные стоимости одного погонного метра тела сооружения. Аналогичным образом рассматривается весь массив заданных типов укреплений и сооружений.
С учетом сказанного и других конструктивно-технических ограничений на основе представленных выше алгоритмов гидравлических расчетов С.П. Паудяль разработаны алгоритм и программа «SUD-ROP» для автоматизированного проектирования комплекса оптимальных сооружений системы поверхностного дорожного водоотвода в неразрывной связи с водосборным бассейном. Основной объединенный алгоритм расчета по данной программе можно изложить в следующем виде:
1. Определяют ось водоотводного тракта в плане от начала водораздела до замыкающего створа русла с учетом рельефа (уклона) и других особенностей местности.
2. Определяют общую конфигурацию водосборного бассейна относительно выбранной оси тракта и осуществляют необходимые операции для выполнения расчета ливневого склонового стока.
3. В зависимости от уклонов, длины участков и других особенностей местности всю протяженность водоотводного тракта по выбранному направлению делят на ряд конструктивных участков. С учетом целесообразности принятия того или иного типа водоотводных сооружений (канавы, кювета, быстротока, перепада), а также необходимых технических ограничений для каждого конструктивного участка задают соответствующий тип сооружений:
CSTYP(m)=l - канава/кювет;
CSTYP(m)=2 - быстроток;
CSTYP(m)=3 - перепад.
4. Задают массив типов укреплений, рассматриваемых при поиске оптимальных решений по каждому из заданных типов сооружений со своими характеристиками, такими как допускаемые скорости, коэффициенты заложения откосов, коэффициенты шероховатости, абсолютные шероховатости, минимально допускаемые уклоны, толщины укреплений, конструктивные запасы, стоимости единичных объемов материалов и т.д.
5. Определяют расчетную продолжительность ливня, предварительно учитывая характеристики наиболее вероятных типов укреплений (осредненный уклон русла, коэффициенты его шероховатости и др.) на каждом конструктивном участке.
6. Определяют оптимальные расчетные интервалы времени для каждой расчетной полосы склона (поскольку эти полосы могут сильно разниться между собой по шероховатости и уклону). Для каждого конструктивного участка русла определяют также два расчетных интервала времени: один - при наименьшем, а другой - при наибольшем значениях коэффициентов шероховатостей заданных типов укреплений и принимают меньший из двух. Окончательно за общий расчетный интервал времени принимают наименьший из всех, - определяемых как для склонового стока, так и для руслового. Затем определяют общее количество расчетных интервалов времени.
7. По полученному оптимальному расчетному интервалу времени определяют соответствующие расчетные интервалы длины для каждой полосы склона и каждого конструктивного участка русла.
8. Разделив длину каждого конструктивного участка русла на соответствующую величину расчетного интервала длины и, округляя до целого числа в сторону увеличения, определяют количество этих интервалов для каждого конструктивного участка.
9. Вводя необходимые исходные данные, производят расчеты согласно приведенному алгоритму и составляют файл данных склонового стока.
10. После этого вводят исходные данные по каждому конструктивному участку и осуществляют непосредственно автоматизированное проектирование оптимальных конструкций сооружений системы поверхностного дорожного водоотвода.
Итогом решения данной задачи является получение типов сооружений (канавы, быстротоки или перепады), размеров поперечных сечений, типов укреплений и объемов работ на каждом конструктивном участке.
Схемы стыковки конструктивных участков (см. рис. 31.1 б,в) определяют с учетом оптимальных поперечных сечений и уклонов смежных конструктивных участков. Каждая отдельная схема на рис. 31.16,в показывает форму перехода от предыдущего конструктивного участка в последующий в зависимости от уклона последнего через соответствующий расчетный интервал длины, а пунктирные линии показывают возможность сохранения предыдущей формы.
На основе экспериментального проектирования комплекса водоотводных сооружений установлено, что применение указанного метода проектирования в ряде случаев дает возможность снизить расчетный расход в среднем до 30 % и строительную стоимость до 50 % по сравнению с традиционной технологией проектирования.
Дата добавления: 2017-03-12; просмотров: 1707;











