Получение параметрических ограничений на основе анализа НИП

Рассмотрим систему, описываемую псевдорегрессионным уравнением, линейным относительно вектора параметров ,

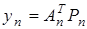, (34)

где 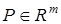— обобщенный вход (регрессор), 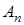принадлежит ограниченной, но априори неизвестной области 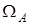. Для системы (34) известна экспериментальная информация

.

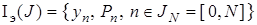Необходимо на основе анализа множества 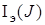для системы (34) определить оценку для области 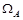, заданной в виде

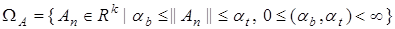
Рис. 10. Система получения текущих оценок нормы вектора
параметров объекта (34)

Предлагаемая процедура нахождения области параметрических ограничений основана на уточнении оценок

,

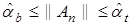где

, .

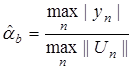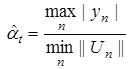на основе анализа информационного портрета. Для этого осуществляется предварительный анализ информационного множества 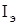и затем определяются обобщенные характеристики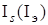

На основе множества 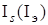формируются переменные 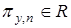, , 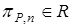равные текущему значению нормы от ,

, ,

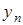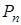
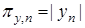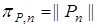где 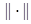— некоторая норма вектора .

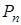Выходом системы (рис. 10) является переменная (коэффициент структурности)

,

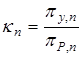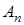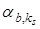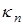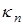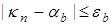которая представляет собой текущую оценку нормы вектора параметров . В качестве возьмем такое значение , лежащее в окрестности среднего значения переменной, , что , где 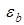— заданное положительное число.

Рис. 11. Информационный портрет, отображающий результаты оценивания параметров области ограничений на основе анализа коэффициента структурности

Построим отображение 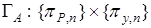на евклидовой плоскости 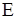. Проведем секущую 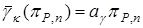, где 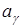— некоторое число. Найдем на плоскости 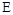точку 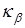пересечения 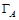и 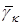, ближайшую к 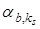. Определим в ее окрестности две ближайшие точки, лежащие слева и справа от 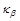на кривой 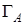, т. е. 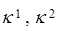. Найдем коэффициент коррекции как 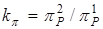. Тогда в качестве 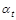можно взять оценку

.

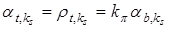Такой выбор точек 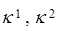объясняется необходимостью получения оценок, близких к .

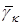После нахождения оценок области 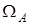следует проверить условия доминирования и найти показатели

,

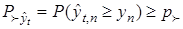
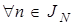где 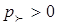— заданная величина.

Результаты определения оценок области 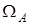показаны на рис. 11.