Числовые характеристики некоторых случайных величин.

Найдем теперь числовые характеристики случайных величин (математическое ожидание, дисперсию и среднее квадратическое отклонение) случайных величин, рассмотренных выше.

1. Распределение Бернулли. Здесь случайная величина 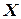- число наступления события Aпри одном испытании, причем 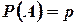. Найти математическое ожидание и дисперсию для этого распределения.

Величина 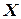принимает два значения 0 и 1 соответственно с вероятностями 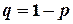и p. Поэтому по формулам (4.1) и (4.6) находим

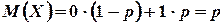
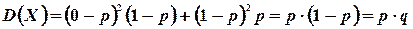
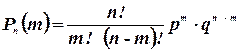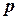2. Биноминальный закон распределения. Определяется формулой Бернулли: , где - постоянная вероятность появления события 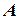в данном конкретном опыте.

Пусть 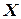- случайная величина, принимающая значения 1 или 0 в зависимости от того, происходит или не происходит событие A в i-м опыте. Тогда 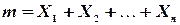. Ясно, что 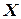попарно независимы. Из результата примера 2 следует, что 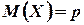, 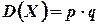для любого 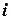. На основании свойства 3° для математического ожидания и дисперсии имеем

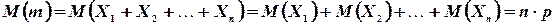
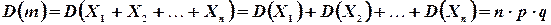
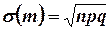
3. Пусть 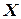- случайная величина, распределенная по закону Пуассона: 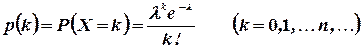. Найт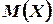и и .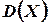

Используя соотношение (4.1), получим

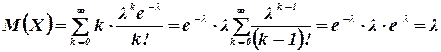
Так как

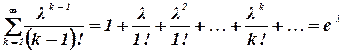
Найдем теперь выражение для дисперсии закона Пуассона

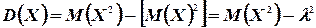
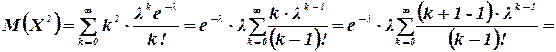
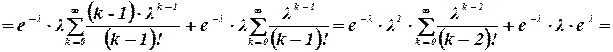
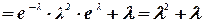
Следовательно,

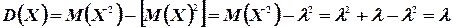
4.Пусть теперь 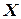- случайная величина, имеющая равномерное распределение с плотностью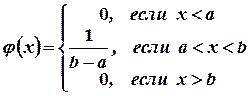

Найдем математическое ожидание, дисперсию и средне квадратическое отклонение этой случайной величины.

По формулам (4.2), (4.7) и (4.11) находим

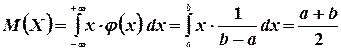
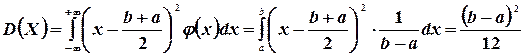
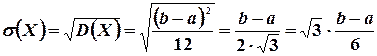
5. Сейчас можно выяснить смысл параметров 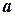и 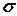нормального закона распределения случайной величины.

Пусть 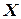- нормально распределенная случайная величина, с параметрам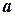и и 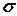. Найдем 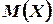и .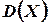

Так как 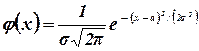, то по формуле (4.2) находим

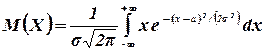
Проведем в интеграле замену переменной, полагая 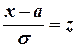. Тогда 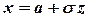, 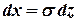. Следовательно,

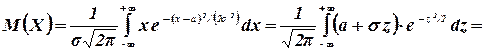
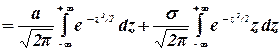
Но

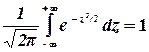
cм. формулу (3.7). Далее, так как функция 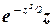нечетная, то по свойству нечетных функций 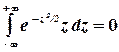. Следовательно, .

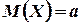Дисперсию находим по формуле (4.7)

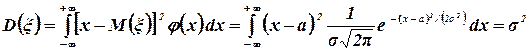
(вычисление интеграла не приводим).

Итак, .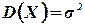

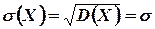Таким образом, параметры 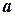и 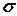для нормально распределенной случайной величины имеют простой вероятностный смысл: a есть математическое ожидание, 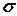- среднее квадратическое отклонение.