Математическое ожидание случайной величины и его свойства.

Рассмотрим сначала следующий пример. Пусть на завод поступила партия, состоящая из Nподшипников. При этом:

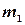- число подшипников с внешним диаметром ,

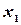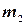- число подшипников с внешним диаметром ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

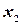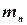- число подшипников с внешним диаметром .

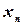Здесь 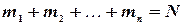. Найдем среднее арифметическое значение 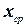внешнего диаметра подшипника. Очевидно,

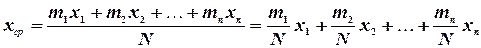
Внешний диаметр вынутого наудачу подшипника можно рассматривать как случайную величину 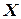, принимающую значения 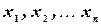, c соответствующими вероятностями 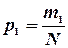, , 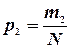..., 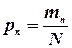, так как вероятность 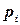появления подшипника с внешним диаметром xiравна mi /N. Таким образом, среднее арифметическое значение xср внешнего диаметра подшипника можно определить с помощью соотношения

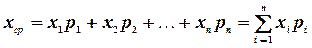
Пусть 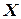- дискретная случайная величина с заданным законом распределения вероятностей 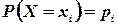(такую таблицу для дискретной случайной величины мы уже приводили):

Значения 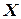х1 х2 . . . хn
Вероятности 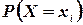p1 p2 . . . pn

Математическим ожиданием дискретной случайной величины 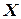называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е.

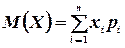(4.1)

В случае, если множество возможных значений дискретной случайной величины образует бесконечную последовательность x1, x2, ..., xn, ..., то математическое ожидание этой случайной величины определяется как сумма ряда 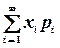, причем требуется, чтобы этот ряд абсолютно сходился.

Возвращаясь к разобранному выше примеру, мы видим, что средний диаметр подшипника равен математическому ожиданию случайной величины 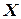- диаметру подшипника.

Математическим ожиданием непрерывной случайной величины 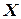с плотностью распределения 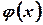называется число, определяемое равенством

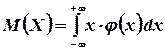(4.2)

При этом предполагается, что несобственный интеграл, стоящий в правой части равенства (4.2) существует.

Рассмотрим свойства математического ожидания. При этом ограничимся доказательством только первых двух свойств, которое проведем для дискретных случайных величин.

1°. Математическое ожидание постоянной С равно этой постоянной.
Доказательство. Постоянную 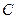можно рассматривать как случайную величину 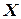, которая может принимать только одно значение 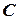c вероятностью равной единице. Поэтому .

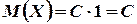2°. Постоянный множитель можно выносить за знак математического ожидания, т.е. .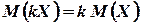

Доказательство. Используя соотношение (4.1), имеем

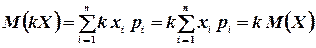
3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

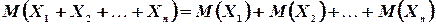(4.3)

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:

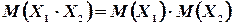(4.4)

Под суммой (произведением) двух случайных величин 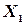и 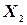понимают случайную величину 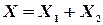, возможные значения которой состоят из сумм (произведений) каждого возможного значения величины 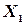и каждого возможного значения величины .

 

 

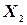2. Дисперсия и ее свойства. Среднее квадратическое отклонение.

Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения 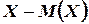случайной величины от ее математического ожидания.

Предварительно рассмотрим пример. Пусть две случайные величины 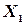и 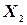заданы следующими рядами распределения

 

Значения 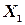-0,2 -0,1 0,1 0,2
Вероятности 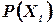0,25 0,25 0,25 0,25
Значения 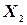-50 -40
Вероятности 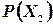0,25 0,25 0,25 0,25

 

Легко убедится в том, что математические ожидания этих величин одинаковы и равны нулю:

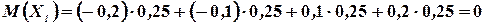
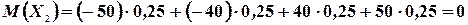
Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной 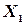, близки к ее математическому ожиданию, а во втором случае далеки от него. Для оценки разброса (рассеяния) значений случайной величины около ее математического ожидания вводится новая числовая характеристика - дисперсия.

Дисперсией 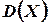случайной величины 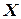называется математическое ожидание квадрата отклонения случайной величины от ее математичеcкого ожидания:

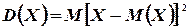(4.5)

Казалось бы, естественным рассматривать не квадрат отклонения, а просто отклонение 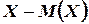случайной величины от ее математического ожидания. Однако математическое ожидание этого отклонения равно нулю, так как

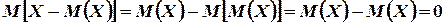
Здесь мы воспользовались тем, что 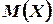постоянно, а математическое ожидание постоянной есть эта постоянная. Можно было бы принять за меру рассеяния математическое ожидание модуль отклонения случайной величины от ее математического ожидания: 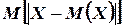. Однако, как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям. Поэтому приняли то, что приняли.

Выведем теперь другую формулу для расчета дисперсии.

Пусть 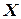- дискретная случайная величина, принимающая значения 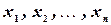соответственно с вероятностями 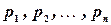. Очевидно, что случайная величина 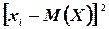принимает значения

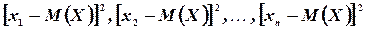
с теми же вероятностями 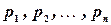. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

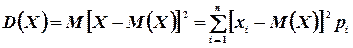(4.6)

Если же 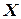- непрерывная случайная величина с плотностью распределения 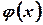, то по определению

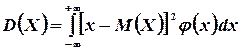(4.7)

Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

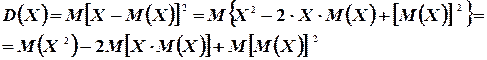
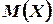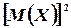Так как и - постоянные, то, используя свойства математического ожидания, получим

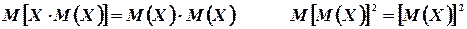
Следовательно,

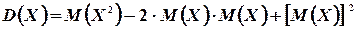
Откуда окончательно находим

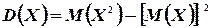(4.8)

 

Рассмотрим теперь свойства дисперсии.

 

1°. Дисперсия постоянной равна нулю.

Доказательство. Пусть 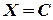. По формуле (4.8) имеем

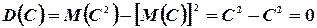
так как математическое ожидание постоянной есть эта постоянная:

2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

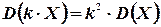(4.9)

Доказательство. На основании соотношения (4.8), можно записать

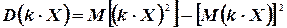
Так как

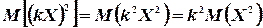
и

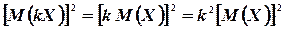
то

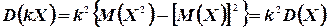
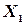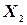3°. Если и - независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий:

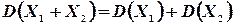(4.10)

Доказательство. По формуле (4.8) имеем

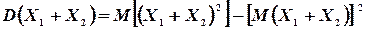
Но

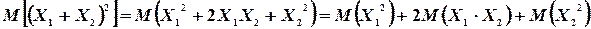
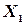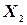Так как и - независимые случайные величины, то

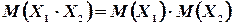
Следовательно

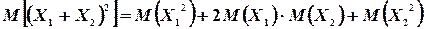
Далее,

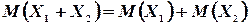
поэтому

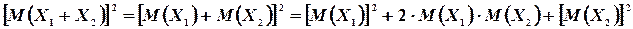
Таким образом

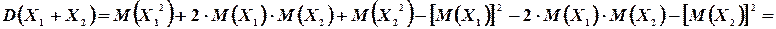
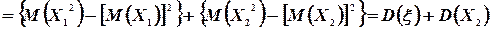
Следовательно

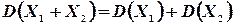
Замечание. Свойство 3° распространяется на любое конечное число попарно независимых случайных величин:


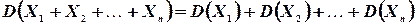
Средним квадратическим отклонением 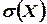случайной величины 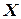называется корень квадратный из ее дисперсии:

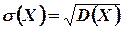(4.11)

Среднее квадратическое отклонение 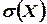имеет ту же размерность, что и случайная величина .

 

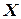Пример 4.1. Случайная величина 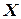- число очков, выпадающих при однократном бросании игральной кости. Определить: математическое ожидание, дисперсию и средне квадратическое отклонение.

Решение: Используя формулы (4.1), (4.6) и (4.11) соответственно получим

 


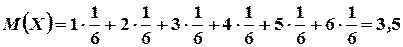
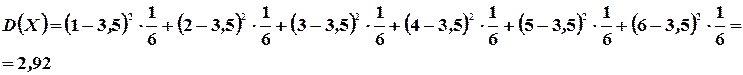
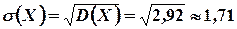
Дата добавления: 2017-02-13; просмотров: 3617;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, добавьте сайт познайка в закладки и расскажите о нем друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2025 год. Материал предоставляется для ознакомительных и учебных целей. Политика конфиденциальности
Генерация страницы за: 0.022 сек.