ПОНЯТТЯ ПРО ТЕОРІЮ ПОДІБНОСТІ ФІЗИЧНИХ ЯВИЩ ТА ЇЇ ЗАСТОСУВАННЯ ДЛЯ РОЗВ’ЯЗУВАННЯ ЗАДАЧ КРИТЕРІЇ ПОДІБНОСТІ.

Найкраще досліджувати фізичні явища, чи процеси в реальних умовах, на натурних зразках. Але така практика не завжди можлива, так як потребує великих матеріальних витрат, та затрат часу.

У дитинстві багато хто будував моделі літаків, кораблів граючи з струмками води будував плотини та водоймища. Досвідчені інженери та конструктори також, перш ніж виготовити велику багатовартісну споруду, наприклад високу телевежу, підводний човен чи систему теплозахисту космічних кораблів, для отримання найоптимальніших характеристик в реальних умовах, спочатку проводять експерименти на моделях. При цьому в експериментах на моделях вимірюють, наприклад в аеродинамічних трубах силу опору повітря для літаків, на пресах – навантаження що руйнують мости чи інші конструкції. Такі експерименти будуть змістовними і корисними для проектування натурних об’єктів лише тоді коли проводяться з урахуванням певних правил моделювання. Інакше результати експериментів використати в проектуванні неможливо.

Головний сенс моделювання полягає у тому, щоб по результатам дослідів, які зручно і з меншими витратами коштів та часу можна виготовити, знайти найкращі параметри об’єкта (процесу), а іноді просто встановити невідомі раніше закономірності.

Встановлення закономірностей за допомогою фізичного моделювання найчастіше є єдиним можливим способом експериментального вивчення і рішення важливих практичних задач. Так при вивченні конвекційного теплообміну між об’єктами, де на процес впливає дуже велика кількість факторів, використання експерименту стає головним джерелом визначення параметрів процесу. Визначені параметри такого процесу можна використати для опису подібного йому явища.

Поняття подібності, що зародилося в геометрії, може бути поширене, узагальнене для різного роду фізичних явищ. З шкільної геометрії відомо, що дві фігури подібні, якщо відношення довжин відповідних сторін однакове, а кути при відповідних сторонах рівні.

· Для отримання фізичної подібності необхідно звернутись до аналізу розмірностей параметрів що характеризують те чи інше явище. Нехай необхідно визначити якусь величину яка залежить функційно від інших параметрів: 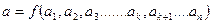;(1), у нашому випадку це може бути коефіцієнт теплообміну ;

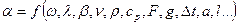де, r( 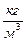)густина; n( 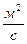)в’язкість(кінематична) l( 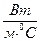)теплопровідність; С_р( 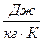)теплоємність; b (^оС^-1) коефіцієнт об’ємного розширення; 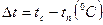(різниця температур поверхні і рідини; 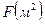площа поверхні; 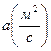коефіцієнт температуропровідності; 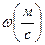швидкість потоку рідини біля поверхні; 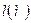геометричний параметр поверхні; 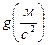прискорення вільного падіння

Якщо функція відображає якусь математичну залежність між величинами, то вона не повинна залежати від вибору одиниць вимірювання. Для отримання наслідку з цього факту розіб’ємо параметри на дві групи. До першої , віднесемо параметри з незалежними розмінностями (розмірність параметра не може бути виражена співвідношеннями інших параметрів даної групи).

До другої всі інші 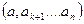. Розмірності параметрів другої групи можуть бути виражені через відношення параметрів першої групи.

Тоді кожен з параметрів другої групи можна виразити у вигляді добутку степенем від розмірності параметрів першої групи.

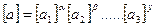
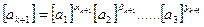;(2)

………………………….

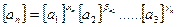
Степені 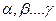отримуються порівняння лівих і правих частин вище записаних рівнянь, при цьому величини:

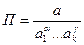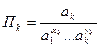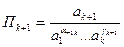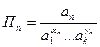, , ,…… ;(3)

Виявляються безрозмірними( чисельники і знаменники мають однакову розмірність), тобто їх значення будуть однакові при будь якому виборі одиниць вимірювання.

Так як (1)не залежить від вибору розмірності, то відповідне ій співвідношення може бути представлене в безрозмірному вигляді:

,

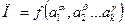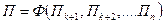;(4),а сама залежність прийме вигляд: 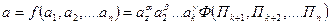;(5)

Тобто наша функція завжди може бути представлена через фунцію меншого числа безрозмірних величин. Це спрощує дослідження. Приведення залежності до безрозмірного вигляду називають пи-теоремою (П- теоремою).

Безрозмірні комплекси П-критерії подібності

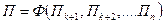- критеріальне рівняння подібності.

Тепер сформулюємо умови фізичної подібності явищ:

Явища повинні відбуватися у геометрично подібних системах

Явища повинні бути якісно однакові і описуватись одними і тими ж параметрами 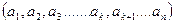, чисельні значення яких можуть відрізнятись у цих явищах, але так щоб безрозмірні числа 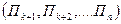співпадали. Ці числа називають параметрами або критеріями подібності явищ.

Для двох подібних фізичних явищ критеріальне рівняння має однаковий вигляд.

Теорія подібності стверджує, що для будь-якого випадку теплообміну існує однозначна залежність між певними величинами, що характеризують процеси теплообміну. Ці комплекси величин і параметри мають однакове значення для всіх подібних процесів і називаються інваріантами, або числами подібності, їх позначають двома початковими буквами імен вчених, що внесли великий вклад у відповідну галузь науки. Для конвекційного теплообміну найбільш важливі такі критерії:

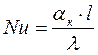; критерій тепловіддачі Нусельта

Характеризує інтенсивність конвекційного теплообміну на кордоні рідини – стінки (відношення кількості теплоти, яка була передана конвекцією, до кількості теплоти, переданою теплопровідністю)

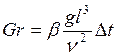; критерій підйомних сил Грасгофа

Визначає відношення під ємної сили, яка була викликана різницею густин холодних та нагрітих частинок рідини та сил молекулярного тертя ( тобто характеризує інтенсивність вільного руху рідини )

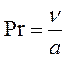; фізичних властивостей речовини (рідини) Прандтля

Є мірою подібності полів температур та швидкостей в потоці рідини, характеризуючи її властивості

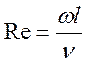; гідродинамічний критерій Рейнольдса

Є мірою відношення сил інерції та в’язкості в потоці рідини, характеризуючи гідродинамічний режим руху потоку рідини

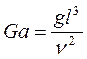; критерій сил тяжіння Галілея

Показує міру відношення сил тяжіння та молекулярного тертя в потоці.

w - швидкість руху рідини в м/с

а – коефіцієнт температуропровідності

Основною задачею-є визначення a_к (коефіцієнту теплообміну), що входить у число Нуссельта.

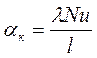
Для визначення Nu складають критеріальне рівняння, яке дозволяє встановити залежність числа Nu від інших чисел подібності

Nu=f(Gr;Pr;Re…)

У критеріальне рівняння входять лише ті числа, які мають суттєве значення для даних умов теплообміну

Висновок: на даному занятті курсантів та студентів було ознайомлено з особливістю передачі тепла конвекцією.

Завдання на самопідготовку:

1. Башкирцев М.П. Основи пожарной теплофизики М.Стройиздат, с. 114-128.

2. Рябова І.Б., Сайчук І.В.,Шаршанов А.Я., термодинаміка і теплопередача в пожежній справі, Харків-2010, с. 80-96.

3. Конспект.