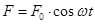Динамическое гашение колебаний
Динамический гаситель, присоединяемый к объекту, формирует дополнительные динамические воздействия. Прикладываемые к объекту в точках присоединения гасителя. Динамическое гашение осуществляется при таком выборе параметров гасителя, при котором эти дополнительные воздействия частично уравновешивают (компенсируют) динамические воздействия, возбуждаемые источником.
Схема простейшего динамического виброгасителя представлена на рис. 12.3
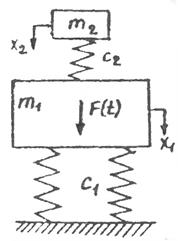 На массу
На массу 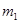 , упруго соединенную с основанием, действует приложенная сила F(t), которую будем в дальнейшем полагать монохроматической.
, упруго соединенную с основанием, действует приложенная сила F(t), которую будем в дальнейшем полагать монохроматической.
|
Рис. 12.3
Задача ставится следующим образом: выяснить возможность снижения амплитуды колебаний массы "m1" за счет введения дополнительной массы "m2" , упруго соединенной с массой m1.С целью упрощения задачи полагаем, что система недиссипативна, т.е. рассеяние энергии в упругих связях не происходит.
Дифференциальные уравнения, описывающие движения масс "ml" и "m2", могут быть записаны в виде:
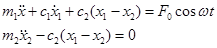 (12.11)
(12.11)
Поскольку система недиссипативна, то колебания отдельных масс либо совпадают по фазе с внешней возмущающей силой, либо находятся с ней в противофазе (сдвиг 180 градусов).
Частное решение системы (12.11) может быть представлено в виде:
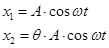 (12.12)
(12.12)
где 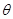 - коэффициент распределения амплитуд колебаний.
- коэффициент распределения амплитуд колебаний.
Величину 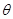 определяем, подставив соотношение (12.12) во второе уравнение (12.11)
определяем, подставив соотношение (12.12) во второе уравнение (12.11)
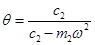 (12.13)
(12.13)
Для искомого периодического решения системы (12.11) справедливо равенство:
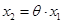 (12.14)
(12.14)
Подставляя (12.14) в первое уравнение системы (12.11) получим:
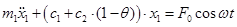 (12.15)
(12.15)
Решение системы линейных дифференциальных уравнений может быть сведено к интегрированию одного линейного дифференциального уравнения второго порядка вида (12.15):
Нетрудно получить
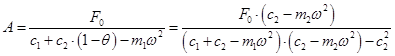 (12.16)
(12.16)
Знаменатель дроби может обращаться в нуль при изменении параметров системы, т.е.
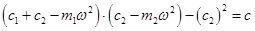
Данное уравнение является частным уравнением системы, у которого два корня 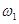 и
и 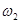 , являющиеся частотами собственных колебаний системы. В нуль может обращаться и числитель дроби в правой части соотношения (12.16),т.е.
, являющиеся частотами собственных колебаний системы. В нуль может обращаться и числитель дроби в правой части соотношения (12.16),т.е.
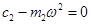 (12.17)
(12.17)
Обозначим эту частоту через 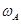 . Очевидно,
. Очевидно, 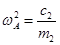
При вьшолнении соотношения (12.17) амплитуда А колебаний массы ml обращается в нуль, и, следовательно, масса ml становится неподвижной.Это явление называется антирезонансом,а частоту 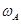 , при которой это происходит - частотой антирезонанса.
, при которой это происходит - частотой антирезонанса.
Частота антирезонансасовпадает с частотой собственных колебаний массы m2 при неподвижной массе ml. Неподвижность массы ml в точке антирезонанса гарантируется только выполнением соотношения (12.17).
Определим амплитуду колебаний массы m2. Из соотношения (12.16) и (12.17) получим:
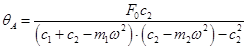
При 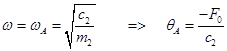
Очевидно, что если масса m2 оказывается малой, то при фиксированной 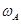 жесткость
жесткость 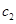 также мала и большой оказывается амплитуда
также мала и большой оказывается амплитуда 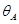 . Чтобы её уменьшить, приходится увеличивать массу m2.
. Чтобы её уменьшить, приходится увеличивать массу m2.
Контрольные вопросы к лекциям N10-12
1. В чём состоит задача уравновешивания?
2. Какие виды неуравновешенности механизмов Вы знаете? Обьясните каждый из них.
3. Сформулируйте условия полного уравновешивания механизмов машины.
4. Что является мерой статической и динамической неуравновешенностей?
5. Расскажите о методе замещающих масс при уравновешивании.
6. С какой целью и как устанавливаются корректирующие массы (противовесы)?
7. Как произвести полное статической уравновешивание (шарнирного четырёхзвенника), кривошипно-ползунного механизма?
8. Сформулируйте, что такое статическая, моментная и динамическая неуравновешенность Вотора?
9. В чём состоят причины дисбаланса вращающихся деталей?
10. На каком принципе работают станки для динамической балансировки?
11. В чём состоит вибрационная защита машин? Какие методы виброзащиты Вы знаете?
12. Какой метод виброзащиты называется виброизоляцией? В чём суть этого метода? В каких случаях он эффективен?
13. Что такое динамическое гашение колебаний? В каких случаях оно применяется?
Дата добавления: 2017-02-13; просмотров: 4124;