Этапы решения задач виброзащиты.

· построение модели объекта;

· формирование критериев качества;

· изучение реакции объекта на заданное внешнее воздействие;

· сравнение по заданному критерию результирующих показателей с допустимыми величинами.

Простейшие задачи виброизоляци возникают в том случае, когда совокупность сил в реальном упругом амортизаторе может быть с достаточной точностью описана как линейная функция координаты х и скорости :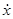

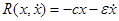(12.3)

Коэффициент "с" принято называть жесткостью амортизатора, а " 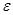" -коэффициент вязкого трения (демпфирования). С учетом (12.3) уравнение (1) примет вид:

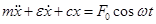(12.4)

Обозначим 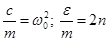и перепишем (12.4) следующим образом:

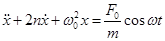(12.5)

Ограничимся анализом работы вибразащитной системы в установившемся режиме. В этом случае решение уравнение (12.5) может быть представлено в виде:

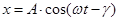(12.6)

где А - амплитуда колебаний массы "m"; 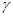- сдвиг фаз между колебаниями массы "m" и внешней силой F(t). При этом амплитуда колебаний:

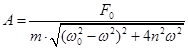(12.7)

и сдвиг фаз колебаний массы 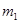и силы F(t):

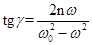
Оценку качества виброизоляции целесообразно проводить, сопоставляя амплитудное значение силы 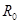, развиваемой в амортизаторе и, следовательно, передаваемой на основание, с амплитудным значением внешней силы .

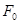Отношение амплитудного значения силы r₀ к амплитудному значению внешней силы F₀, называется коэффициентом виброизоляции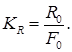

Амплитудное значение силы, развиваемой в упругом амортизаторе:

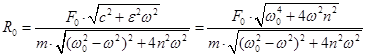
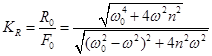(12.8)

Используя понятие относительного коэффициента затухания 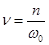можно привести выражение 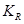к виду, удобному для анализа:

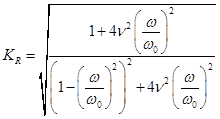(12.9)

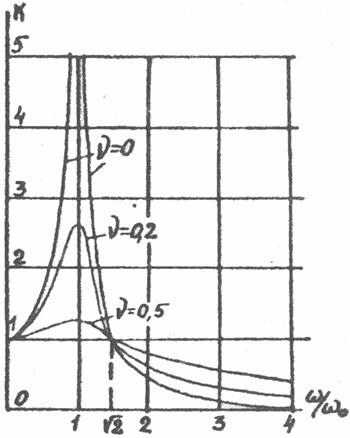Из анализа выражения (12.9) видно, что коэффициент виброизоляции 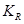явным образом зависит от соотношения частот (вынужденной и собственной). Для различных соотношений: 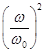- (расстройка) и 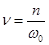построены графики:

Условие эффективности виброзащиты :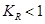

· Виброизоляции эффективна при любом 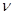в диапазоне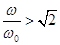

· При 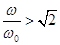чем меньше 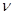, тем эффективнее виброизоляция.