Метод кінцевих різниць

2.Нехай є необмежена плоска стіна товщиною 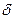. Розглянемо розв’язок рівняння для знаходження температурного поля в даній стінці.

Розділимо стіну на шари однакової товщини 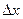, які пронумеруємо від 1 до k. Час також розіб’ємо на інтервали довжиною 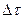.Тоді крива неперервна лінія, що виражає зміну температури по товщині стінки, замінюється ламаною лінією.

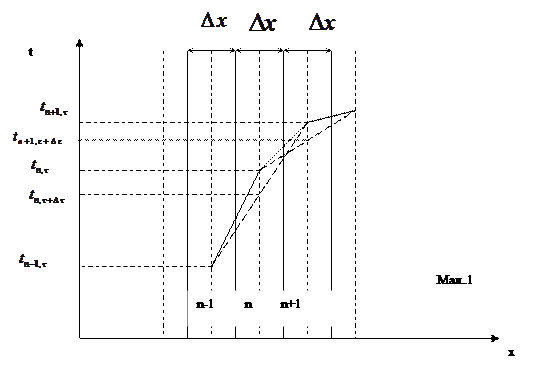
Розглянемо три довільні шари стінки (n-1), n, (n+1). Як видно з малюнку в межах шару n лінія розподілення температури має два нахили, тому і похідна температури по координаті буде мати два значення:

;

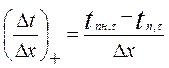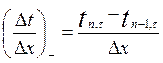
Для другої похідної в кінцевих різницях отримаємо наступний вираз:

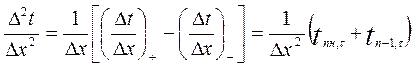
Зміна температури за час 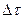в середині шару n рівна:

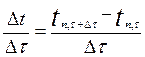
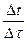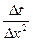Після підстановки виразів і в рівняннях отримано:

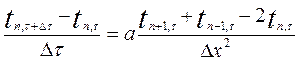
звідси

(**)

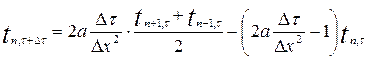Відповідно, якщо відомо розподілення температур по товщині тіла в момент часу τ, то по рівнянню (**) можна знайти розподілення температури в послідуючий інтервал часу τ+Δτ, і так далі.

Для даного тіла з певним значенням коефіцієнта температуропровідності, інтервали часу Δτ і товщину шару Δх можна вибрати так, щоб

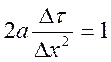, тоді рівняння (**) буде мати вигляд: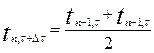

Дане рівняння показує, що температура в центрі будь якого шару n в послідуючий інтервал часу рівна середньоарифметичному значенню температур взятих в центрах суміжних шарів в попередній інтервал часу.

Геометричний зміст формули полягає у тому, що з’єднавши відрізками температури стінки через шар отримаємо точки перетину відрізків з осьовими лініями шарів. Ці точи визначатимуть температури у відповідних шарах в наступний інтервал часу τ+Δτ.