Неуравновешенность роторов и их балансировка

Рассматриваемая задача является вторым основным направлением, разработанным в теории уравновешивания, ее существо несколько отлично от первой, уже разобранной. В ней рассматриваются условия рационального подбора масс звеньев механизма, которые обеспечили бы полное или частичное уменьшение динамических давлений на некоторые кинематические пары механизма. Уравновешивание (балансировка) вращающихся масс приобрело особое значение в современных условиях. Так, в турбинах и гироскопах частота вращения достигает 30000 об/мин, веретена суперцентрифуг вращаются со скоростями до 50000 об/мин и выше. При скоростях, даже меньше указанных, от небольшого смещения центра масс с геометрической оси вращения возникают совершенно непредвиденные конструктором значительные силы инерции, вызывающие появление больших динамических давлений в опорах, следствием чего является ряд нежелательных вибрационных явлений в машине, ее раме или даже фундаменте.

В теории уравновешивания ротором называют любое вращающееся материальное тело независимо от его технического назначения (коленчатый вал, рабочее колесо турбины, якорь электродвигателя, магнитный диск для записи информации в ЭВМ и т. д.)

Если вращение ротора сопровождается появлением динамических реакций его подшипников, что проявляется в виде вибрации станины, то такой ротор называется неуравновешенным. Источником этих динамических реакций является главным образом несимметричное распределение массы ротора по его объему.

В зависимости от взаимного расположения оси вращения О-О и главной центральной оси инерции I-I различают следующие виды неуравновешенности роторов:

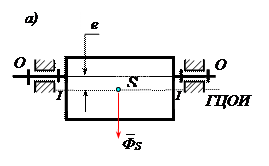
- Статическую (рис. 11.1 а), когда ось вращения и главная центральная ось инерции параллельны;

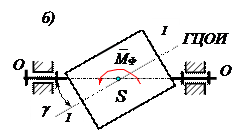
- Моментную(рис. 11.1 б), когда оси пересекаются в центре масс ротора S;

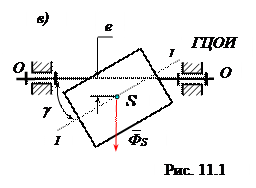
- Динамическую(рис. 11.1 в), когда оси либо пересекаются вне центра масс, либо перекрещиваются.

Если масса ротора распределена относительно оси вращения равномерно, то главная центральная ось инерции совпадает с осью вращения и ротор является уравновешенным или идеальным.

Различают две группы роторов: жесткие и гибкие.

Ротор относится к категории жестких, если на всем диапазоне скоростей вращения до значения рабочей (эксплуатационной) скорости деформации упругой линии вала ротора незначительны.

При значительных деформациях его следует считать гибким. Практика машиностроения большинство роторов характеризует как жесткие. Жесткий ротор допустимо рассматривать как твердое тело, к которому при его исследовании применимы закономерности механики твердого тела.

Из теоретической механики известно, что давление вращающегося тела на его опоры в общем случае складывается из двух составляющих: статической, обусловленной действием заданных сил и динамической, обусловленной ускоренным движением материальных частиц, из которых состоит вращающееся тело (ротор). У неуравновешенного ротора динамическая составляющая не равна нулю.

Рис. 11.2

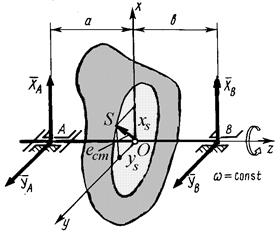
При равномерном вращении ротора вокруг оси z (рис. 11.2) проекции динамической составляющей определяются следующим образом:

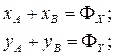(11.1)

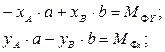(11.2)

Эти проекции главных векторов и главных моментов сил инерции подсчитываются по формулам:

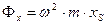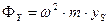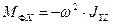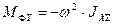; ; ; (11.3)

В этих зависимостях:

m- масса ротора; J_YZ, J_XZ – центробежные моменты инерции ротора относительно системы координат OXYZ.

Плоскость XOY проходит через центр масс ротора, а вся система вращается вместе с ротором. Отметим, что в рассматриваемой динамической задаче главный момент сил инерции ротора 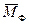есть величина векторная.

Неуравновешенность ротора (как следует из уравнений (11.3)) возрастает пропорционально квадрату его угловой скорости. Поэтому если быстроходные роторы неуравновешенны, то они оказывают на свои опоры динамические давления, вызывающие вибрацию стойки и ее основания. Устранение этого вредного воздействия называется балансировкой (уравновешиванием) ротора. Решение данной задачи относится к динамическому проектированию машин.

Модуль главного вектора центробежных сил инерции ротора составит: 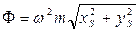. В векторном виде ,

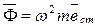где e_ст – статический эксцентриситет массы ротора (радиус-вектор центра масс ротора)

Мерой статической неуравновешенности ротора является статический дисбаланс

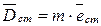(11.4)

Вектор 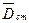называется главным вектором дисбалансов ротора. Очевидно, что .

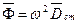Модуль главного момента центробежных сил инерции 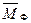ротора составит: 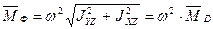; , (11.5)

Главный момент дисбалансов ротора: .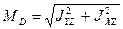

Так как неуравновешенность определяется конструктивными характеристиками ротора или механизма и не зависит от параметров движения, то при балансировке оперируют не инерционными силами `Ф и моментами 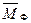, а пропорциональными им дисбалансами 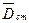и моментами дисбалансов`M_D.

Балансировкой называют процесс определения значений и угловых координат дисбалансов ротора и их уменьшения с помощью корректировки размещения его масс. Балансировка эквивалентна уравновешиванию системы инерционных сил, прикладываемых к подвижному ротору для его равновесия.