Определение эквивалентного диаметра

Из уравнения пропускной способности 1.73 запишем выражение для определения разницы квадратов давления в любом подучастке трубопровода:

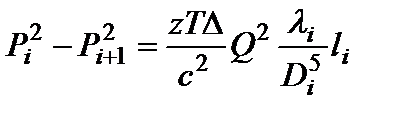(1.74)

Подставив (1.74а) в (1.74) и приняв z, T и D постоянными величинами, получим:

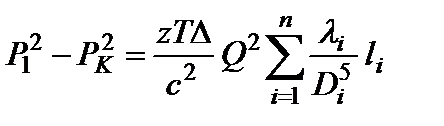. (1.75)

С другой стороны, приняв, что участок имеет постоянный диаметр D_ЭК, можно записать: 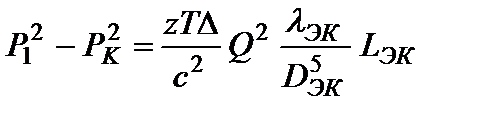, (1.76)

где: L_ЭК - длина рассчитываемого участка, .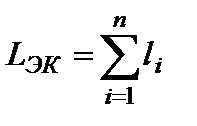

Приравняв правые части уравнений (1.75) и (1.76), получаем:

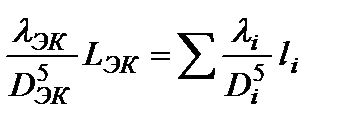(1.77)

откуда 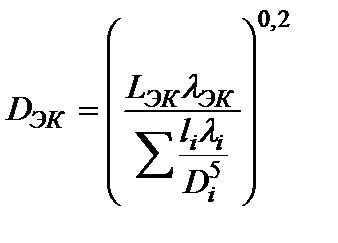. (1.78)

Для квадратичного режима течения газа в участке, с учетом уравнения 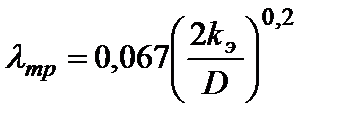, величина 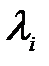обратно пропорциональна 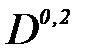, следовательно, выражение (1.77) примет следующий вид: 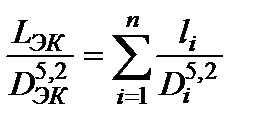. (1.79)

В этом случае получаем: 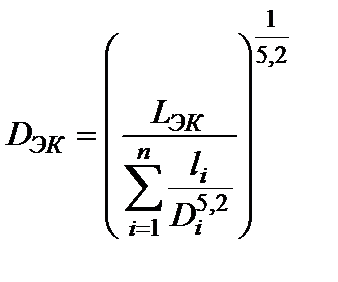. (1.80)

В полученном соотношении 2 неизвестных D_ЭК, L_ЭК, как правило, задаются 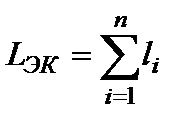и тогда D_ЭК находится легко.

Определение коэффициента расхода.

Используя уравнение расхода:

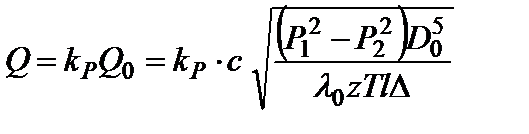, (11)

где: Q₀ - пропускная способность эталонного трубопровода), получим зависимость для определения разности квадратов давления в подучастке:

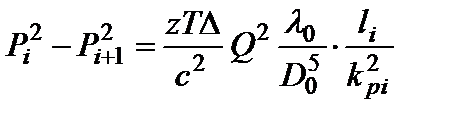, (1.81)

Тогда для всего участка: 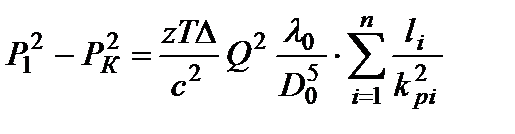, (1.82) или используя уравнение (11): 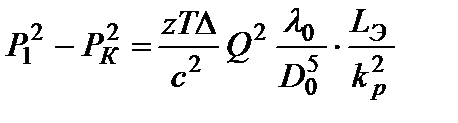. (1.83)

Приравняв правые части уравнений (1.82) и (1.83) получаем:

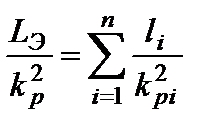, (1.84), откуда 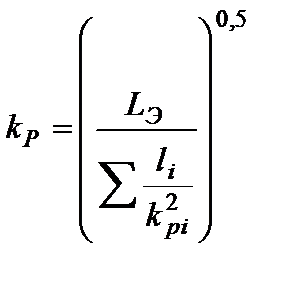. (1.85)