Теоретические основы расчета висячих мостов
Особенности деформирования висячих мостов
Принципиальным отличием статического расчета висячих мостов от расчета других конструкций является необходимость рассчитывать их по деформированной схеме. В литературе встречаются и другие названия: расчет с учетом геометрической нелинейности, расчет с учетом прогибов, деформационный расчет.
Суть геометрической нелинейностилегче всего выяснить на простом примере с консольной балкой (рис. 12.1). Сначала дадим определение: геометрическая нелинейность - это свойство конструкций, которое заключается в том, что величина внутренних усилий (М, Q, N) зависит от деформированного положения сооружения (т.е. от прогибов).
Для большинства конструкций величины hв, hг (см. рис. 12.1, а) столь незначительны, что ими пренебрегают и определяют внутренние усилия по исходной, недеформированной схеме (обычный линейный расчет, известный по курсу сопротивления материалов, - рис. 12.1, б).
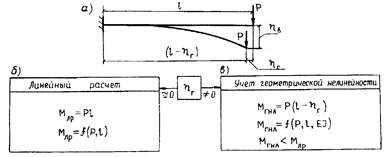
Рис. 12.1. Иллюстрация расчета конструкций по деформированной схеме
Если перемещения hв, hг существенны, то величина Мгнл зависит от деформированного положения конструкции, т. е. от ее жесткости (рис. 12.1, в):
Мгнл = Р(l - hг) или Мгнл = f(P, l, EI). (12.1)
Попутно заметим, что учет геометрической нелинейности для большинства конструкций, оказывается, выгоден, так как Мгнл < Млр (см. рис. 12.1, б, в), т.е. сооружение можно запроектировать более легким.
Как известно, висячий мост можно смоделировать балкой на двух опорах, если ее подкрепить вместо подвесок упругими опорами типа пружин с реакцией Rj (рис. 12.2). Получается, действительно, «замкнутый круг»: пока мы не знаем величины hj, мы не можем найти реакции опор Rj, а с другой стороны, пока неизвестны реакции Rj, нельзя найти прогибы балки hj (см. рис. 12.2). Единственным выходом из этого «круга» является метод последовательных приближений или итераций. Следовательно, итерационным путем необходимо найти такие прогибы hj*, чтобы соответствующие им Rj* обеспечивали равновесие балки под нагрузкой.
На рис. 12.3, а условно показан итерационный процесс поиска деформированного положения конструкции h* по спирали «с избытком-с недостатком», начиная от исходного положения h = 0. На рис. 12.3, б приведен график, иллюстрирующий итерационный процесс, который можно считать завершившимся, если разница двух соседних итераций окажется меньше некоторой малой величины e:
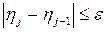 , (12.2)
, (12.2)
где j - номер итерации.
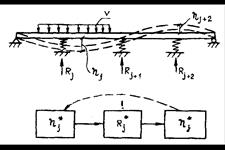
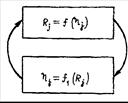
Рис. 12.2. Иллюстрация к итерационному процессу поиска
деформированного положения конструкции
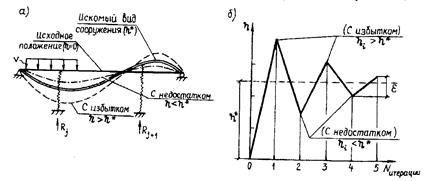
Рис. 12.3. Иллюстрация к итерационному процессу учета
геометрической нелинейности
Но не только к итерационным процессам приводит расчет по деформированной схеме. Гораздо большие трудности в дальнейшем доставит нарушение принципа независимости действия сил, что влечет за собой невозможность использования линий влияния для висячих мостов.
Особенности деформирования висячей конструкции рассмотрим при помощи рис. 12.4.
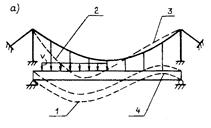
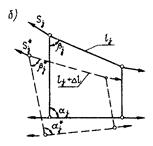
Рис. 12.4. Особенности деформирования висячих мостов
Существуют причины, требующие для висячих мостов учета геометрической нелинейности:
1. Повышенная деформативность элементов. Это обусловлено применением высокоэкономичных систем и высокопрочных материалов с пониженным значением модуля упругости.
2. При загружении половины пролета для висячих мостов характерен S-образный изгиб (рис. 12.4, а). Под действием нагрузки левая часть балки жесткости прогибается (1). Вслед за ней опускается вниз левая часть кабеля (2) - в этот момент срабатывает «эффект нити»: правая часть кабеля распрямляется (3). При этом кабель поднимается вверх, через подвески заставляя изгибаться балку жесткости (4). Таким образом, балка жесткости принимает необычную форму равновесия (см. рис. 12.4, а).
В этом случае жесткость конструкции оценивается по амплитуде перемещений точек балки:
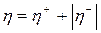 . (12.3)
. (12.3)
Поэтому загружение половины пролета для большинства элементов висячих мостов гораздо опаснее, чем всего пролета, в отличие от других систем.
3. Повышенная чувствительность висячей конструкции к искажениям геометрической схемы (рис. 12.4, б). Значительные удлинения гибких элементов 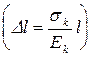 сочетаются с существенными изменениями углов (
сочетаются с существенными изменениями углов ( 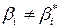 ), на величину которых влияют и горизонтальные перемещения узлов.
), на величину которых влияют и горизонтальные перемещения узлов.
Обзор методов деформационного расчета висячих мостов
Все известные методы расчета можно разделить на две группы.
1. Аналитические методы, возникшие в 1880-1890 гг. и широко применявшиеся до 60-х гг. нынешнего столетия. Большой вклад в их развитие внесли зарубежные ученые: Мюллер-Бреслау, Д. Мелан, Д. Штейнман, Ф. Блейх, Р. Пагслей, С. Тимошенко и российские ученые: В. Гастев, Н. Кирсанов, И. Дуров, С. Степкин и другие [Смирнов В.А. Висячие мосты больших пролетов. 2-е изд., перераб. и доп. М.: Высш. школа, 1975. 368 с., Кирсанов Н.М. Висячие системы повышенной жесткости. М.: Стройиздат, 1973. 116 с., Общая система уравнений для стержневых систем и ее решение на ЭВМ: Метод. указ. / Сост. С.П. Васильев, Е.В. Васильков. Новосибирск, 1988. 50 с., Цаплин С.А. Висячие мосты. М.: Дориздат, 1949. 217 с.].
2. Численные методы, появившиеся в 60-е гг. и связанные с развитием ЭВМ. В их становлении принимали участие отечественные и зарубежные ученые: В. Смирнов, А. Петропавловский, В. Никифоров, В. Фридкин, Т. Поскит, Г. Веет, А. Робинсон, Н. Хироши и многие другие [Проектирование металлических мостов / Под ред. А.А. Петропавловского. М.: Транспорт, 1982. 320 с., Смирнов В.А. Висячие мосты больших пролетов. 2-е изд., перераб. и доп. М.: Высш. школа, 1975. 368 с., Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Пыринов Б.В., Бахтин С.А. Уточненный способ деформационного расчета комбинированных систем висячих мостов // Исследования работы искусственных сооружений. Новосибирск, 1980. С. 34-41., Описан С.С. Оптимизация металлических комбинированных предварительно напряженных конструкций. Киев, 1984. 82 с., Дуров П.С. Деформационный расчет висячих мостов с использованием ЭВМ // Тр. Новочеркасск. политехн. ин-та. Т 232. Новочеркасск, 1971. С. 3-7., Фридкин В.М. О построении алгоритмов расчета висячих и вантовых комбинированных конструкций с учетом геометрической нелинейности // Исследования и разработки по висячим и вантовым металлическим конструкциям. М., 1980. С. 114-122.].
В аналитических методах используется континуальная (т.е. непрерывная) модель. Это означает, что реальная конструкция заменяется условной, для которой принимается ряд допущений, упрощающих ее работу:
1) действие подвесок на балку жесткости принимается в виде равномерно распределенной нагрузки, направленной вверх (это и дало название - континуальная модель);
2) линейные деформации подвесок и кабеля принимаются равными нулю (Dl = 0);
3) не учитываются горизонтальные перемещения кабеля;
4) поперечные сечения балки жесткости и кабеля принимаются постоянными по всей длине моста и т. д.
Идея большинства аналитических методов заключается в разделении исходной висячей конструкции на две подсистемы: балку жесткости и кабель, связь между которыми компенсируется реакцией подвесок в виде равномерно распределенной нагрузки интенсивностью z (рис. 12.5).
Для каждой подсистемы составляются уравнения равновесия элемента в дифференциальной форме (см. рис. 12.5). Расчет сводится к решению системы дифференциальных уравнений и к использованию дифференциальных зависимостей между расчетными факторами прогибом, изгибающим моментом в балке, поперечной и продольной силами.
Совместное решение уравнений основано на допущении равенства вертикальных перемещений балки и кабеля (hk = hб) за счет нерастяжимости подвесок (Dl = 0) и отсутствия горизонтальных смещений.
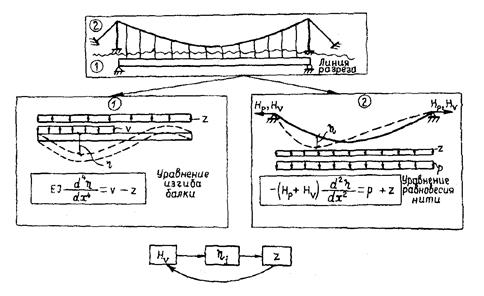
Рис. 12.5. Общая схема аналитических методов расчета висячих мостов
Однако для решения системы уравнений недостаточно применения только математических методов интегрирования дифференциальных уравнений. Это объясняется тем, что в двух уравнениях (см. рис. 12.5) содержится три группы неизвестных: распор от временной нагрузки Нv, усилия в подвесках z и прогибы h. Поэтому задача интегрирования уравнений должна сочетаться с итерационным процессом поиска деформированного вида сооружения. Именно в этом и заключается различие в решении поставленной задачи разными авторами.
Методы расчета висячих мостов в отдельности не будем рассматривать, но отметим, что во многих из них в качестве критерия сходимости итерационного процесса используется коэффициент деформативности, введенный Н. Кирсановым:
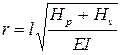 . (12.4)
. (12.4)
Если конструкция жесткая (Е1 ® ¥), то (r ® 0) и можно выполнять линейный расчет. При r ³ 2...3 конструкция становится достаточно гибкой и расчет требуется вести по деформированной схеме. В реальных висячих мостах величина r* колеблется от 2 до 20. Итерационный процесс поиска r* происходит аналогично рис. 3.3, б - от r = 0 по спирали «с избытком - с недостатком». Найдя r*, можно определить Нv* и раскрыть систему уравнений, вычислив z* и h*.
На рис. 12.6 показаны графики поправочных коэффициентов mi = f(r) для оценки влияния деформационного расчета [Кирсанов Н.М. Висячие системы повышенной жесткости. М.: Стройиздат, 1973. 116 с.].
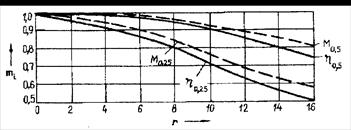
Рис. 12.6. Поправочные коэффициенты mi, для приближенного учета
геометрической нелинейности висячих мостов
Вполне очевидны недостатки, присущие аналитическим методам:
1) наличие многих допущений дает заметную погрешность и даже искажает картину фактической работы;
2) расчет ведется только на отдельные загружения моста временной нагрузкой, при которых удобно интегрировать уравнения;
3) при расчете упускается часть параметров (число подвесок, их длина, наклон, площадь поперечного сечения пилонов и т.д.).
В связи с этим были разработаны численные методы деформационного расчета висячих мостов. Они основаны на дискретной модели, т. е. состоящей из отдельных элементов, более приближенной к реальной конструкции. Наибольшее распространение из них получили смешанный метод и метод дополнительных параметров жесткости, являющийся модификацией метода перемещений [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с.]. Общий подход для численных методов следующий:
- записываются уравнения равновесия узлов в деформированном состоянии (рис. 12.7):
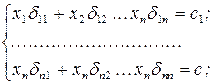
- составляется система конечно-разностных уравнений, учитывающих нелинейность перемещений и записываемых, как правило, в матричной форме;
- решается система уравнений на ЭВМ с учетом итерационных процессов поиска деформированного вида.
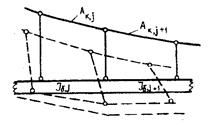
Рис. 12.7. Общая схема численных методов расчета
Таким образом, за счет учета многих факторов (горизонтальных перемещений, удлинения элементов, переменности их сечения и т.д.) удается добиться высокой точности расчетов.
Определение невыгодных (опасных) загружений висячих мостов
временной подвижной нагрузкой
Суть проблемы состоит в невозможности использования при расчете висячих мостов, как в конструкциях, работающих линейно, аппарата линий влияния. Существует несколько способов поиска невыгодных загружений для висячих мостов. Рассмотрим четыре из них, причем в порядке повышения точности.
Способ 1-й - по двум характерным загружениям: на весь пролет (l = l) и на половину пролета (l = 0,5l) (рис. 12.8). Загружение всего пролета (рис. 12.8, б) дает в первом приближении максимальный изгибающий момент в середине балки жесткости М1. Второе загружение (рис. 12.8, в) позволяет получить близкие к экстремальным значения изгибающих моментов (М2, М3) в четвертях пролета.
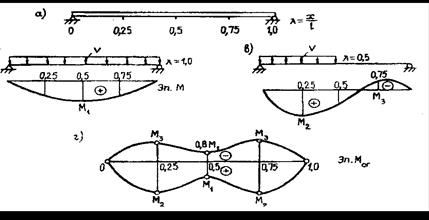
Рис. 12.8. Построение огибающей эпюры Мог в балке по двум характерным загружениям
Точности данного способа вполне достаточно для построения огибающей эпюры Мог изгибающих моментов в балке, например, при курсовом проектировании (рис. 12.8, г).
Отметим, что в отличие от большинства конструкций балка жесткости висячего моста работает, во-первых, в каждом сечении на изгибающие моменты двух знаков (т.е. изгибается и вверх и вниз) и, во-вторых, наиболее напряженно в четвертях пролета (Мmax = М0,25).
Данные загружения висячего моста нормативной временной нагрузкой дают и экстремальные значения прогибов: при l = l получается максимальный прогиб в середине пролета (h0,5), при l = 0,5l возникает максимальный прогиб в четверти пролета (h0,25) и минимальный - в сечении 0,75l (h0,75). Как правило, второе загружение гораздо опаснее при проверке жесткости пролетного строения, так как
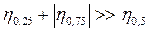 . (12.5)
. (12.5)
Способ 2-й - по линиям влияния, построенным методами строительной механики для висячих мостов, как для обычных стержневых систем без учета геометрической нелинейности. Для этого с некоторой долей приближения следует принять жесткости элементов (Elб, EkAk) стремящимися к бесконечности.
Полученные при помощи традиционных линий влияния невыгодные загружения будут, безусловно, точнее, чем в способе 1 (см. рис. 12.8). На рис. 12.9 приведены очертания линий влияния и соответствующих невыгодных загружений для середины и четверти пролета по материалам Г. Передерия и В. Качурина.
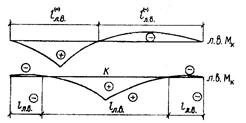
Рис. 12.9. Линии влияния изгибающих моментов
в балке висячего моста, построенные как для
обычных стержневых конструкций
Способ 3-й- по «функциям влияния» или «фундаментальным функциям», построенным по аналогии с линиями влияния, но с косвенным учетом геометрической нелинейности (Н. Кирсанов, И. Дуров). В частности, найденные длины невыгодных загружений по данному способу будут в большей мере зависеть от жесткости пролетного строения (например, от коэффициента деформативности r), и поэтому диапазон их значений еще шире:
- для К = 0,25: lдлв(+) = (0,37...0,46)l, lдлв(-) = (0,54...0,63)l;
- для К = 0,5: lдлв(+) = (0,25... 0,81)l.
Способ 4-й - поисковый метод при помощи ЭВМ. Программа варьирует положение временной нагрузки на пролетном строении и отбирает наиболее опасные ее положения, причем расчет ведется по деформированной схеме, т.е. с учетом всех жесткостных показателей. Результатом подобного варьирования параметров стали графики (рис. 12.10, а, б), по которым, например, можно определить, что для сечения в четверти пролета (K = 0,25) длина невыгодного загружения составляет lнз(+) = 0,25...0,42 в зависимости от жесткости пролетного строения. Далее были построены графики функций 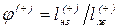 и
и 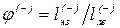 для значений К = 0...1,0, отражающих различные положения сечения балки (рис. 12.10, в, г). Графики данных функций j = f(K) можно легко аппроксимировать при помощи многочленов n-й степени:
для значений К = 0...1,0, отражающих различные положения сечения балки (рис. 12.10, в, г). Графики данных функций j = f(K) можно легко аппроксимировать при помощи многочленов n-й степени:
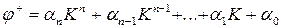 .
.
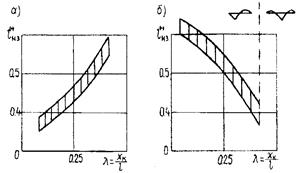
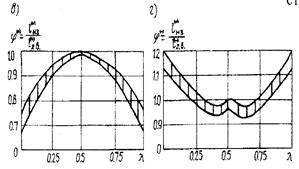
Рис. 12.10. Графики зависимостей длин невыгодных загружений временной
нагрузкой висячих мостов от положения сечения, полученные поисковыми
методами на ЭВМ
Тогда можно получить длину невыгодных загружений:
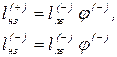
для любого значения К = 0...1,0.
Проведенная предварительная работа по способу 4 позволяет построить огибающую эпюру Мог с весьма высокой точностью с учетом геометрической нелинейности, используя алгоритм, представленный на рис. 12.11.
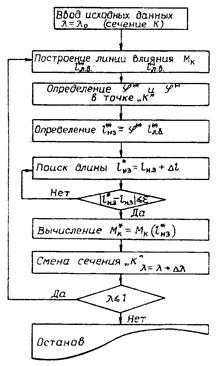
Рис. 12.11. Укрупненная блок-схема алгоритма построения
огибающей эпюры Мог в балке жесткости точным способом
Заключение. На основании сравнения результатов, полученных рассмотренными способами, сформулируем некоторые выводы.
1) Невыгодные положения временной подвижной нагрузки, найденные разными способами, принципиально не отличаются друг от друга (одинаковое количество участков, большинство опасных загружений начинается от одной из опор и т.д.).
2) Длина участков невыгодных загружений существенно отличается в зависимости от способа определения (0,5l; lлв, lдлв, lнз - до 15...30 %). Интересно отметить, что для первых трех способов, естественно, сумма длин участков невыгодных загружений для одного сечения К равна длине пролета 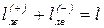 . Но сумма соответствующих значений, найденных четвертым, точным способом, меньше длины пролета
. Но сумма соответствующих значений, найденных четвертым, точным способом, меньше длины пролета 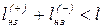 .
.
3) Несмотря на существенное различие в длинах невыгодных загружений ( 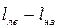 ), отличие в абсолютных значениях найденных по ним изгибающих моментов в балке на порядок меньше (до 5...10%). Таким образом, невыгодные загружения висячих мостов подвижной нагрузкой можно искать одним из рассмотренных способов в зависимости от требуемой точности расчетов.
), отличие в абсолютных значениях найденных по ним изгибающих моментов в балке на порядок меньше (до 5...10%). Таким образом, невыгодные загружения висячих мостов подвижной нагрузкой можно искать одним из рассмотренных способов в зависимости от требуемой точности расчетов.
Практический расчет висячих мостов на ЭВМ
Статический расчет висячих мостов можно разделить на два этапа:
1) построение графиков внутренних усилий (М, N) и перемещений (h) аналогично рис. 13.7 и 13.8 при помощи различных программ для ЭВМ;
2) уточнение размеров поперечных сечений несущих элементов (кабеля, балки жесткости, пилонов, подвесок) на основе их проверок по прочности, жесткости, выносливости.
Отсутствие эпюр поперечных сил в балке жесткости на рис. 13.7, 13.8 объясняется тем, что их величины в висячих мостах весьма незначительны, и проверку по прочности по касательным напряжениям можно не проводить. Напомним, что подвески играют роль упругоподатливых опор, и эпюры поперечных сил имеют «пилообразный» вид.
На первом этапе статического расчета висячих мостов рекомендуется использовать один из существующих сегодня вычислительных комплексов для ЭВМ (ЛИРА, PACK, РК, СПРИНТ, МКЭСС и т.д.).
Напомним, что кабель, пилоны и подвески работают на постоянную и временную нагрузки (опасное загружение - весь пролет l = l). Балка жесткости воспринимает только временную нагрузку и наиболее интенсивно работает при загружении половины пролета (l = 0,5l).
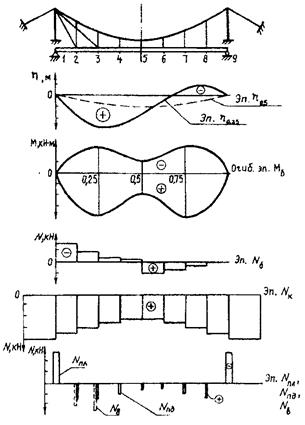
Рис. 13.7. Примеры построения графиков внутренних усилий
и перемещений (М, N, h) для висячего моста
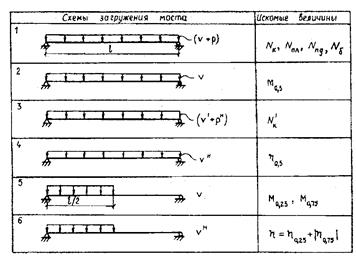
Рис. 13.9. Схемы загружения висячего моста для расчета на ЭВМ
В связи с этим в случае, если есть возможность проведения не менее шести расчетов на ЭВМ, предлагается следующий порядок расчета (рис. 13.9):
- первое загружение (v + р, l = l) дает максимальные Nк , Nпл, Nпд,
- второе загружение (v, l = l) - максимальный M0,5,
- третье загружение (v'+ рн, l = l) - для расчета на выносливость Nk';
- четвертое загружение (vн, l = l) - максимальный h0,5;
- пятое загружение (v, l = 0,5l) - максимальный М0,25, минимальный М0,75;
- шестое загружение (vн, l = 0,5l) - максимальную амплитуду: 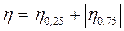 прогибов.
прогибов.
В случае, если по техническим причинам при курсовом проектировании возможен лишь один расчет на ЭВМ, то в качестве единственного загружения резонно выбрать пятое (см. рис. 13.9). Тогда результаты данного расчета необходимо откорректировать так, как показано на рис. 3.21, чтобы кроме найденных сразу М0,25, М0,75 определить с некоторым приближением Nк, Nпл, М0,5, h, Nк', Nпд, Nб.
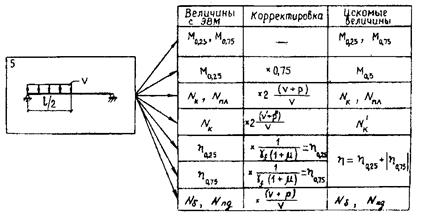
Рис. 13.10. Схема загружения висячего моста для получения приближенных результатов
Первый этап статического расчета висячих мостов завершается построением графиков М, N, h) (см. рис. 13.7).
Второй этап следует начать с оценки жесткости пролетного строения в целом. Для этого сравниваются полученные при расчете величины: амплитуда h и максимальный прогиб в середине пролета h0,5 с допустимым прогибом [D]:
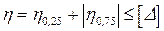 , (13.4)
, (13.4)
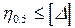 . (13.5)
. (13.5)
Если выполняются обе проверки (13.4) и (13.5), то заданные в расчете на ЭВМ значения АкЭВМ и IбЭВМ достаточны для обеспечения жесткости. При дальнейшем подборе сечения кабеля и балки по прочности значения АкЭВМ и IбЭВМ можно уменьшать лишь при наличии определенного запаса по проверкам (13.4) и (13.5).
В случае невыполнения проверки по жесткости (13.4) необходимо увеличить момент инерции балки жесткости, так как именно он в большей степени влияет на величину h:
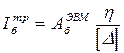 . (13.6)
. (13.6)
Если не выполняется проверка (13.5), то следует увеличить площадь сечения кабеля:
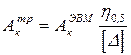 . (13.7)
. (13.7)
Проверка (13.5) не выполняется обычно только при ошибке в задании АкЭВМ, как правило, h >> h0,5. При расчете по одному загружению (рис. 13.10) проверка (13.5) опускается.
При дальнейшем подборе сечений балки и кабеля по прочности следует иметь в виду, что значения АкЭВМ и IбЭВМ, определенные по формулам (13.6) и (13.7), уменьшать нельзя.
Подбор сечений кабеля и подвесок выполняется как для канатов из условия прочности и выносливости. Сначала следует для каждого гибкого элемента задаться конкретными размерами сечений канатов при помощи табл. 13.1, где даны выписки из ГОСТов. Далее принятое сечение проверяется на прочность по СНиП, п. 4.33:
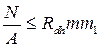 , (13.8)
, (13.8)
где N, А - соответственно усилие и площадь сечения гибкого элемента (табл. 13.1); Rdh - расчетное сопротивление каната, определяется по формуле:
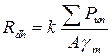 ,
,
где SPun - разрывное усилие каната в целом (табл. 13.1), k, m, m1, gm - коэффициенты, принимаемые по СНиП.
После необходимой корректировки сечения гибкого элемента при расчете на прочность (13.8) проводится его проверка на выносливость по формуле:
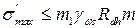 , (13.9)
, (13.9)
где s'max - максимальное напряжение цикла при расчете на выносливость от усилия N'к, полученного в результате загружений № 3 по рис. 13.9 или № 4 по рис. 13.11; gws, m - коэффициенты, принимаемые по СНиП.
Для нахождения коэффициента асимметрии цикла r величину smin можно принять: 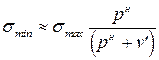 ,
,
так как минимальное усилие в кабеле и подвесках будет только при действии нормативной постоянной нагрузки рн.
Подбор сечения пилона начинается с уточнения его размеров. Напомним, что размеры поперечного сечения стоек принимаются в пределах 1/20...1/30 их высоты, толщина стенок металлических пилонов - 12...20 мм, железобетонных - 250... 500 мм. В курсовом проекте можно ограничиться подбором сечения стойки по устойчивости:
- для металлического пилона по СНиП, п. 4.36
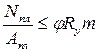 , (13.10)
, (13.10)
- для железобетонного пилона по СНиП, п. 3.69, а.
Рекомендуется найти критическую силу Ркр из расчета пилона методами теории устойчивости в двух плоскостях: как сжатого стержня вдоль моста и как рамы - поперек моста.
Таблица 13.1
Некоторые данные о канатах заводского изготовления
| Диаметр каната, мм | Расчетная площадь, см2 | Масса 100 м каната, кг | Расчетное разрывное усилие каната, кН | ГОСТ |
| 5,5 | 0,181 | 15,8 | 27,7 | ГОСТ 3062-80. Канат одинарной свивки (1+6), диаметр 0,65...11,5 мм |
| 8,0 | 0,380 | 33,0 | 58,2 | |
| 9,8 | 0,573 | 49,9 | 82,6 | |
| 1,017 | 87,3 | ГОСТ 3063-80. Канат одинарной свивки (1+6+12), диаметр 1,6...19 мм | ||
| 1,538 | 132,0 | |||
| 2,167 | 185,5 | |||
| 2,625 | ГОСТ 3064-80. Канат одинарной свивки (1+6+12+18), диаметр 1,6...27 мм | |||
| 22,5 | 2,985 | |||
| 24,0 | 3,370 | |||
| 29,5 | 3,96 | ГОСТ 3081-80. Канат двойной свивки (6(1+9+9)+(1+9+9)), диаметр 6,4...45,5 MM | ||
| 34,0 | 5,36 | |||
| 40,5 | 7,33 | |||
| 45,5 | 9,35 | |||
| 30,5 | 6,17 | ГОСТ 3090-73. Канат закрытый с одним слоем Z-образной проволоки | ||
| 6,74 | ||||
| 7,40 | ||||
| 35,5 | 8,00 | |||
| 38,5 | 10.15 | ГОСТ 7675-73 (действует до 1.07.95). Канат закрытый с одним слоем клиновидной и Z-образной проволоки | ||
| 40,5 | 11,27 | |||
| 42,5 | 12,23 | |||
| 45,0 | 13,58 | |||
| 47.0 | 14,76 | |||
| 51,0 | 17,02 | |||
| 19,88 | ГОСТ 7676-73 (действует до 1.07.95). Канат закрытый с двумя рядами клиновидной и одной Z-образной проволоки | |||
| 20,16 | ||||
| 24.08 | ||||
| 27.63 | ||||
| 32,31 |
Подбор сечения балки жесткости заключается в уточнении размеров, принятых при вариантном проектировании. В случае увеличения Iб по формуле (13.6) следует заново подобрать поперечное сечение балки жесткости такое, чтобы Iб ³ Iбк. Для расчета сталежелезобетонных балок допускается заменять железобетонную плиту металлической с приведенной площадью:
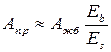 , (13.11)
, (13.11)
где Еb, Еs - модули упругости бетона и металла.
Полученное сечение балки жесткости проверяется на прочность как элемент, работающий на изгиб с растяжением (сжатием) - рис. 13.7, эпюры Мб, Nб СНиП, п. 4.28:
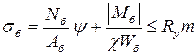 . (13.12)
. (13.12)
Особое внимание следует уделить величине Nб, которая подставляется в формулу (13.12). Дело в том, что для висячих мостов с наклонными подвесками или вантами, с прикреплением кабеля к балке продольную силу Nб, передаваемую на балку жесткости, следует принимать от загружения нагрузкой (р + v), схема №1 по рис. 13.9. Это объясняется тем, что при использовании временных шарниров при монтаже изгибающие моменты в балке жесткости от постоянной нагрузки не возникают, но при этом продольные силы Nб, передаваясь через шарниры, будут действовать от суммарной нагрузки (р + v).
Если подобранные значения Ак и Iк будут существенно (более 20...30%) отличаться от введенных в расчет на ЭВМ (АкЭВМ и IбЭВМ), то расчет желательно повторить.
| <== предыдущая лекция | | | следующая лекция ==> |
| Специфические принципы физического воспитания (принципы, выражающие специфические закономерности занятий физическими упражнениями) | | | Теоретические основы расчета вантовых мостов |
Дата добавления: 2021-06-28; просмотров: 1167;











