Определение температур в детали

При анализе температур в зоне обработки на операциях алмазного выглаживания необходимо, прежде всего, рассматривать деталь, так как именно к качеству ее поверхностного слоя предъявляются основные технологические требования.

Общее распределение температур в детали при выглаживании определяется суммой всех действующих в зоне обработки источников:

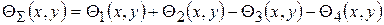, (15.9)

где Θ₁(x,y) - распределение температур, возникающее под действием источника теплоты q₀₁в зоне пластической деформации на передней поверхности индентора; Θ₂(x,y) - под действием источника теплоты q₀₂ в зоне упругого восстановления на задней поверхности индентора; Θ₃(x,y) - под действием стока теплоты из детали в инструмент на передней поверхности индентора q₁; Θ₄(x,y) - под действием стока теплоты из детали в инструмент на задней поверхности индентора q₂.

При описании температурного поля в детали в соответствии с методом источников используются известное аналитическое выражение для полосового быстродвижущегося источника, в котором его ограниченность по ширине учитывается поправочным коэффициентом К_о (в области практически применяемых условий выглаживания принимается K_о = 0,87):

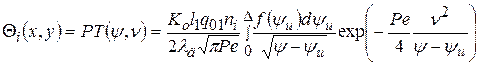. (15.10)

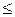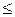где ψ = x/l₁, ψ_u= x_u/l₁, ν = y/1_l, - безразмерные координаты; n_i = q_i/q₀₁- безразмерные величины, учитывающие различие тепловых потоков: n₁ = 1, n₂ = q₀₂/q₀₁, n₃ = q₁/q₀₁, n₄ = q₂/q₀₁; D - верхний предел интеграла: D = y при 0 y 1 и D = 1 при y > 1; f(y_и) - закон распределения плотности теплового потока; P = K_оl₁q₁/2l_д(pРе)⁰⁵ - размерный коэффициент; 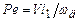- критерий Пекле.

Закономерности формирования температур на поверхности детали (y = 0) при выглаживании, возникающих под воздействием различных тепловых потоков, представлены на рис. 15.4. Распределение температур Θ₁(x,y) соответствует нормальному несимметричному закону распределения плотности теплового потока с функцией распределения f(y_u) = exp[-3(1 - y_u²)], распределение Θ₂(x,y) - нормальному несимметричному закону распределения f(y_u) = exp[-3y_u²]. Общее распределение температур под воздействием источников теплоты q₀₁в зоне пластической деформации и источника теплоты q₀₂ в зоне упругого восстановления Θ₁₂(x,y) = Θ₁(x,y) + Θ₂(x,y), причем тепло от источника на задней поверхности индентора не распространяется на переднюю поверхность.

Распределения температур Θ₃(x,y) и Θ₄(x,y) соответствуют равномерному закону распределения плотности теплового потока с функцией f(y_u) = 1. Общее распределение температур под воздействием источников теплоты на передней q₁и задней q₂ поверхностях индентора Θ₃₄(x,y) = Θ₃(x,y) + Θ₄(x,y), причем тепло от источника на задней поверхности индентора также не распространяется на переднюю поверхность.

Графики суммарного распределения температур по поверхности детали представлены на рис. 15а). Температуры Θ₃₄(x,y) условно показаны в области отрицательных значений, так как тепловые потоки q₁ и q₂ направленыпротивоположно потокам q₀₁ и q₀₂. Следовательно, за счет стока теплоты в инструмент деталь охлаждается.

Представленные зависимости позволяют установить координаты точек на поверхности детали, имеющих максимальную температуру. Для нормального несимметричного, а также для равномерного законов распределения плотности теплового потока с функциями распределения f(y_u) = exp[-3(1 - y_u²)] и f(y_u) = 1 наибольшее значениебезразмерной температурыдостигается при безразмерных координатах y = 1 и n = 0.

В результате расчетов определена максимальная температура Θ_Σmax (x,y) = 347,8^оС при значениях x = 1₁ и y = 0.

Лекция 16.Определение тепловых потоков и температур при