Прямые частного положения

Как уже отмечалось, к прямым частного положения относятся прямые уровня, т.е. параллельные плоскости проекций (в соответствии с рисунком 1.3.1 это прямые h, f, p), и проецирующие прямые, т.е. перпендикулярные плоскости проекций (в соответствии с рисунком 1.3.1, прямые i, q, p’).

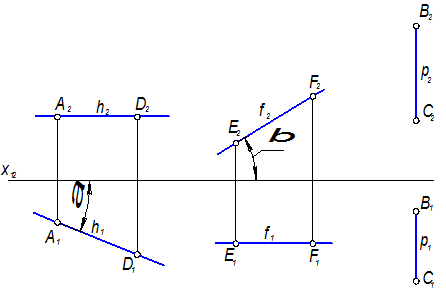
Прямая, параллельная горизонтальной плоскости проекций П₁, называется горизонталью и обозначается на чертеже через h. Так как все точки горизонтали имеют одну и ту же высоту, то её фронтальная проекция h₂ располагается на комплексном чертеже параллельно оси х₁₂, а на горизонтальную плоскость проекций данная прямая проецируется в натуральную величину в соответствии с рисунком 1.3.3. Также в натуральную величину на плоскость П₁ проецируется угол a наклона горизонтали h к фронтальной плоскости проекций П₂: А₁D₁=АD; (h₁ Ùх₁₂)=a.

Прямая, параллельная фронтальной плоскости проекций П₂, называется фронталью и обозначается на чертеже через f. Так как все точки фронтали имеют одну и ту же глубину, то её горизонтальная проекция f₁ располагается на комплексном чертеже параллельно оси х₁₂, а на фронтальную плоскость проекций данная прямая проецируется в натуральную величину (рисунок 1.3.3). Также в натуральную величину на плоскость П₂ проецируется угол b наклона фронтали к горизонтальной плоскости проекций П₁: E₂F₂=EF; (f₂Ù х₁₂)=b.

Прямая, параллельная профильной плоскости проекций, называется профильной прямой и обозначается на чертеже через р. Так как все точки профильной прямой имеют одну и туже широту, то её горизонтальная р₁ и фронтальная р₂ проекции располагаются на комплексном чертеже перпендикулярно оси х₁₂ в соответствии с рисунком 1.3.3, а в натуральную величину данная прямая проецируется на профильную плоскость проекций П₃. На эту же плоскость проекций спроецируются в натуральную величину углы наклона профильной прямой р соответственно к плоскостям проекций П₁ и П₂. Следует заметить, что для определения профильной прямой необходимо задать на проекциях р₁ и р₂ прямой р проекции её двух точек, например В и С (рисунок 1.3.3). Для прямых h и f это делать совсем не обязательно. Обычно при решении различных вопросов с профильными прямыми прибегают к построению третьей проекции на профильную плоскость проекций П₃. Прямая i, перпендикулярная горизонтальной плоскости проекций П₁, называется горизонтально проецирующей прямой. Она проецирует все свои точки на плоскость П₁ в одну точку i₁, которая является её горизонтальной проекцией в соответствии с рисунком 1.3.4 Фронтальная проекция i₂ прямой i перпендикулярна оси х₁₂. Прямая i, будучи параллельной плоскости проекций П₂, проецируется на эту плоскость без искажения, т.е. АВ=А₂В₂. Точки А и В, как имеющие одну и ту же горизонтальную проекцию i₁ºA₁ºB₁, являются горизонтально конкурирующими.

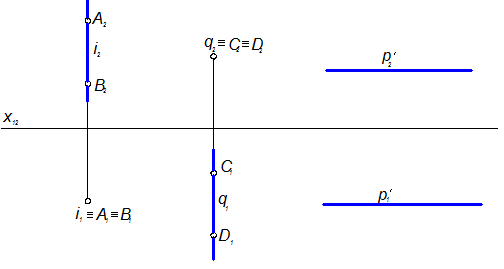Рисунок 1.3.3 – Прямые уровня

Рисунок 1.3.4 – Проецирующие прямые

Аналогично, прямая q, перпендикулярная фронтальной плоскости проекций П₂, проецирует все свои точки, в том числе и точки С и D (рисунок 1.3.4) на плоскость проекций П₂ в одну точку: q₂ºС₂ºD₂. Эта прямая называется фронтально проецирующей прямой. Горизонтальная проекция q₁ прямой q перпендикулярна оси х₁₂. Прямая q, будучи параллельной плоскости проекций П₁, проецируется на неё без искажения, т.е. СD=C₁D₁. Точки С и D, как имеющие одну и ту же фронтальную проекцию q₂ºC₂ºD₂, являются фронтально конкурирующими.

Прямая р¢, перпендикулярная профильной плоскости проекций П₃, проецирует все свои точки в одну на эту плоскость проекций. Эта прямая называется профильно проецирующей прямой. Горизонтальная р¢₁ и фронтальная р¢₂ проекции прямой р¢ параллельны оси х_12. Так как прямая р¢ параллельна плоскостям проекций П₁ и П₂, то она проецируется на эти плоскости без искажения, т.е. р’=р¢₁=р¢₂.

Следы прямой линии

Точки пересечения прямой линии с плоскостями проекций называются следами прямой.

Точка пересечения прямой с горизонтальной плоскостью проекций называется горизонтальным следом прямой Н, с фронтальной плоскостью – фронтальным следом – F.

Пусть прямая АВ общего положения пересекает плоскость П₁ в точке Н и плоскость П₂ в точке F (рисунок 1.3.5).

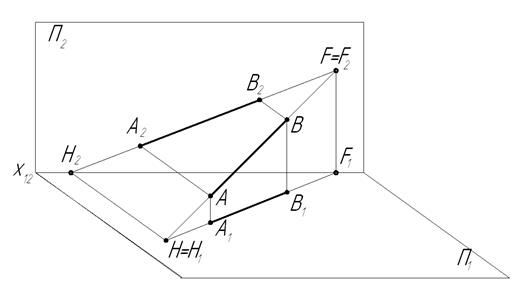
Рисунок 1.3.5 – Следы прямой

Учитывая, что следом прямой является точка, одновременно принадлежащая и прямой, и плоскости проекций, можно наметить правила построения следов.

Горизонтальный след.

Фронтальная проекция горизонтального следа Н₂ является точка пересечения фронтальной проекции прямой с осью х₁₂.

Горизонтальная проекция горизонтального следа Н₁ строится на горизонтальной проекции прямой при помощи вертикальной линии связи, проведенной из Н₂.

Фронтальный след.

Горизонтальной проекцией фронтального следа F₁ является точка пересечения горизонтальной проекции прямой с осью х₁₂.

Фронтальная проекция фронтального следа F₂ строится на фронтальной проекции прямой при помощи вертикальной линии связи, проведенной из F₁.

Рассмотрим на примере принцип построения следов прямой АВ на комплексном чертеже (рисунок 1.3.6).

Для построения горизонтального следа прямой продолжим А₂В₂ до пересечения с осью х₁₂. Точка пересечения будет фронтальной проекцией горизонтального следа Н₂. Из точки Н₂ восстановим перпендикуляр к оси х₁₂. Точка пересечения этого перпендикуляра с продолжением А₁В₁ будет горизонтальной проекцией горизонтального следа Н₁ .

Для построения проекций фронтального следа F продолжим А₁В₁ до пересечения с осью х₁₂. Точка пересечения будет горизонтальной проекцией фронтального следа F₁. Из точки F₁ проведем перпендикуляр к оси х₁₂. Точка пересечения этого перпендикуляра с продолжением А₂В₂ будет фронтальной проекцией фронтального следа F₂ .

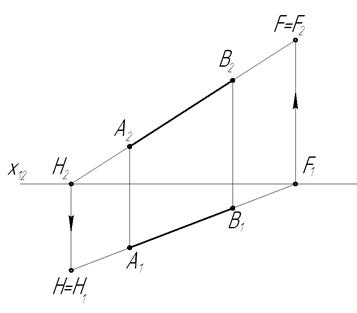
Рисунок 1.3.6 – Построение следов на комплексном чертеже