Параллельное проецирование

Наглядность - ценное свойство центрально проекционных изображений. Однако на практике большое значение имеют и другие качества проекционных чертежей, в частности, простота построения и обратимость. В этом отношении центрально проекционные чертежи не являются наиболее удобными. Поэтому большим распространением пользуется способ параллельного проециро­вания для построения изображений пространственных фигур.

Задаём некоторую плоскость П′, являющуюся плоскостью проекций, и направление проецирования s, не параллельное плоскости проекций П′ в соответствии с рисунком 1.2.2. Для проецирования какой-либо точки А пространства проводим через неё про­ецирующую прямую АА′, параллельную направлению проецирования s. Точка пересечения А′ проецирующей прямой с плоскостью П′ являетсяпараллельнойпроекцией точки А на плоскость П′.

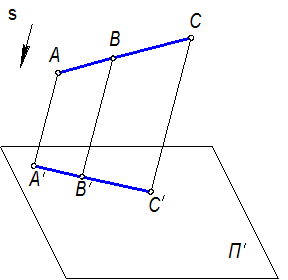Рисунок 1.2.2 – Параллельное проецирование

На рисунке 1.2.2 изображена операция параллельного проецирования отрезка АС. Проецирующие линии всех точек этого отрезка лежат в одной (проецирующей) плоскости. Поэтому проекцией отрезка АС является отрезок А'С' прямой линии. Это свойство общее для центральной и параллельной про­екций.

Рассмотрим некоторые свойства параллельного проецирования, которых не имеет центральная проекция.

1) Прямые, параллельные в пространстве (в общем случае) проецируются в виде прямых, параллельных на плоскости проекций П′.

Пусть имеем прямые АВ и CD, параллельные в пространстве (рисунок

1.2.3).

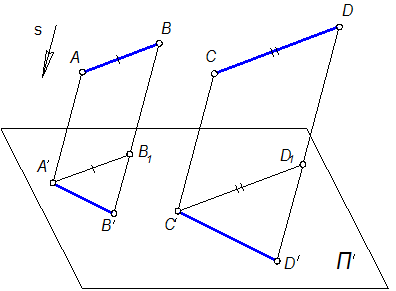
Рисунок 1.2.3 – Параллельная проекция параллельных в пространстве

прямых

Построив для прямых АВ и CD проецирующие плоскости AА¢В¢B и CС¢D¢D, заметим, что эти плоскости параллельны, как плоскости, имеющие уг­лы с соответственно параллельными сторонами (AB||CD; BВ¢ ||DD¢ ). Поэтому проецирующие плоскости пересекают плоскость проекций П' по двум парал­лельным между собой прямым.

2) Отношение отрезков, лежащих на параллельных прямых, со­храняется в параллельной проекции.

Пусть АВ и CD – отрезки, лежащие на параллельных прямых. Построим их проекции на плоскость П¢ при направлении проецирования s (рисунок 1.2.3). Про­ведём в проецирующих плоскостях отрезки А¢В1 и С¢D1, соответственно парал­лельные и равные отрезкам АВ и СD. Треугольники А¢B¢B1 и С¢D¢D1 являются подобными, т.к. их соответственные стороны параллельны. Отсюда

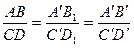В частном случае данные отрезки АВ и CD могут оказаться лежащими на
одной прямой, однако это не изменит рассуждения.

Если при этом концы двух отрезков совпадают, т.е. имеем отрезки АВ и ВС в соответствии с рисунком 1.2.4, то вышеприведённое соотношение примет вид

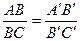Отсюда следует, что отношение, в котором точка В делит отрезок АС. со­храняется в проекции для точки В′, делящей отрезок А'С′.

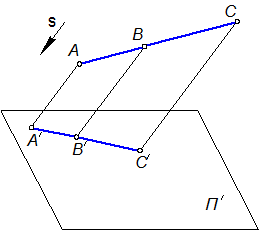Рисунок 1.2.4 – Деление отрезка в заданном соотношении при параллельном проецировании

3)Отношение проекции отрезка А'В' к натуральному отрезку постоянно для всех параллельных между собой отрезков.

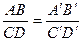Полученная выше пропорция после перестановки крайних членов имеет вид

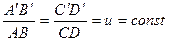Постоянное отношение u называется показателем искажения для отрезков данного направления