Соотношения неопределённости Гейзенберга

В классической механике состояние материальной точки (классической частицы определяется заданием значений координат, импульса, энергии и т.д.). Микрообъекту не могут быть приписаны перечисленные переменные. Однако, информацию о микрочастицах мы получаем, наблюдая их взаимодействие с приборами представляющие собой макроскопические тела. Поэтому результаты измерений поневоле выражаются в терминах, разработанных для характеристики макротел, следовательно, приписываются и микрочастицам. Например, говорят о состоянии электрона, в котором он имеет какое-то значение энергии или импульса.

Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных получается при измерениях точные значения. Так, например, электрон (и любая другая микрочастица) не может одновременно иметь точных значений координаты х и компоненты импульса Р_х. Неопределённость значений x и Р_х удовлетворяет соотношению:

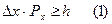
Из уравнения (1) следует, что чем меньше неопределённость одной из переменных, тем больше неопределённость другой. Возможно, такое состояние, в котором одна из переменных имеет точное значение, другая переменная при этом оказывается совершенной неопределенной (ее неопределённость равна бесконечности).

– классические в механике пары называются

канонически сопряженными

т.е.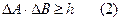

Произведение неопределённостей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка .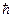

Гейзенберг (1901-1976 гг.), немец, Нобелевский лауреат 1932 г., в 1927 г. сформулировал принцип неопределенности, ограничивающий применение к микрообъектам классических понятий и представлений:

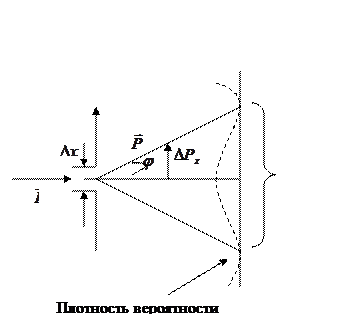
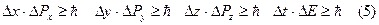
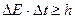– это соотношение означает, что определение энергии с точностью до 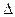E должно занять интервал времени, равный по меньшей мере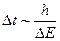

Попытаемся определить значение координаты х свободно летящей микрочастицы, поставив на ее пути щель шириной 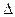х, расположенную перпендикулярно к направлению движения частицы. До прохождения через щель, Р_х=0 Þ 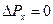, зато координата х является совершенно неопределенной. В момент прохождения щель положение меняется. Вместо полной неопределенности х появляется неопределенность 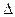х, но это достигается ценой утраты определенности значения P_х. Вследствие дифракции появляется некоторая вероятность того, что частица будет двигаться в пределах угла 2j, j – угол, соответствующий первому дифракционному min (интенсивностью высших порядков можно пренебречь).

Краю центрального дифракционного max (первому min) получающемуся от щели шириной х, соответствует угол j, для которого

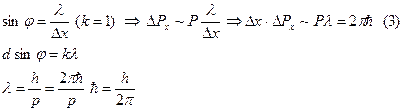
Соотношение неопределённости показывает в какой мере можно пользоваться понятиями классической механики, в частности, с какой степенью точности можно говорить о траектории микрочастиц.

Подставим вместо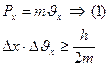

Мы видим, что чем больше масса частицы, тем меньше неопределённости её координаты и скорости, следовательно, c тем большей точностью применимо для неё понятие траектории.

Соотношение неопределённости является одним из фундаментальных положений квантовой механики.

В частности, оно позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме.

Если бы электрон упал на ядро, его координаты и импульс приняли бы определенные (нулевые) значения, что несовместимо с принципом неопределенности (доказательство от обратного).

Пример Хотя соотношение неопределённости распространяется на частицы любых масс, для макрочастиц оно принципиального значения не имеет. Например, для тела m=1 г., движущегося с 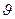=600 м/с, при определении скорости с очень высокой точностью 10^-6 %, неопределенность координаты:

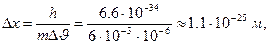т.е. очень и очень мала.

Для электрона движущегося с (что соответствует его энергии в 1эВ).

При определении скорости с точностью до 20%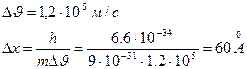

Это очень большая неопределенность, т.к. расстояние между узлами кристаллической решетки твердых тел порядка единиц ангстрем.

Таким образом, любая квантовая система не может находится в состояниях, в которых координаты ее центра инерции (для частицы – координаты частицы) и импульс одновременно принимает вполне определенные значения.

В квантовой механике теряет смысл понятие траектории, т.к. если мы точно определим значения координат, то ничего не можем сказать о направлении ее движения (т.е. импульса), и наоборот.

Вообще говоря, принцип неопределенности справедлив как для макро-, так и для микрообъектов. Однако для макрообъектов значения неопределенности, оказывается пренебрежимо малыми по отношению к значениям самих этих величин, тогда как в микромире эти неопределённости оказываются существенными.