Гипотеза де Бройля. Корпускулярно волновой дуализм микрочасктиц.

Материальные частицы обладают волновыми свойствами. Этот простой экспериментальный факт, широко известный в настоящее время. Вспомним, однако, что в свое время волновые свойства электрона оказались большой неожиданностью. Причина удивления кроется в том, что физики привыкли считать электрон во всем подобным классической частице. Ранние опыты с электронами не противоречили такой модели и до 1927 г. не было ясных экспериментальных указаний на волновые свойства электрона. Теория, выдвинутая Бором (постулаты Бора) для водородоподобных атомов, полностью всех удовлетворяла.

Волновые свойства фотона были открыты раньше, чем его корпускулярные свойства. Изучение электрона шло в обратном порядке. Такая историческая последовательность привела к тому, что у неспециалистов стало почти всеобщим представление, что свет состоит из волн, а электроны являются частицами. В будущем, несомненно, станет общеизвестным, что фотоны, электроны и вообще все частицы похожи друг на друга в том смысле, что обладают некоторыми свойствами волн и некоторыми свойствами корпускул.

В 1924 г. Луи-де-Бройль выдвинул смелую гипотезу, что дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение.

«В оптике, – писал он, – в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалось ли в теории вещества обратная ошибка?». Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де Бройль перенес на случай частиц вещества те же правила, какие справедливы в случае света. Фотон обладает энергией 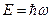и импульсом 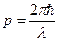. По идеи де-Бройля, движение электрона или какой либо другой частицы связано с волновым процессом, длина волны которого:

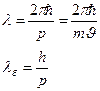
Гипотеза де-Бройля вскоре была подтверждена экспериментально в 1927 г. опытами Н.Дэвиссона и О.Джернера и независимо Г.Томсоном. В опытах Дэвиссона и Джермера изучалось отражение электронов от поверхности кристаллов (монокристаллы никеля кубической системы). Томсон наблюдал прохождение электронов через тонкие кристаллические пленки, были получены дифракционные картины. Таким образом эти опыты подтвердили волновые свойства электрона.

Как рассуждал де-Бройль?

Если с какой либо частицей связана волна, можно ожидать, что она будет перемещаться в том же направлении, что и сама частица. Представим нашу волну функцией x и t, т.е. S(x,t), где S–смещение частиц из положения равновесия, x – расстояние от источника волны, t- время.

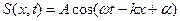– уравнение плоской волны, где

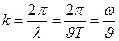– волновое число,

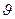– скорость распространения фронта волны

ω – частота

В комплексном виде, по формуле Эйлера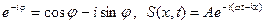

Наша задача – попытаться угадать связь между параметрами k и ω, характеризующими волну, и параметрами P, E и m характеризующими частицу:

Фаза колебаний плоской волны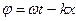

Управление плоскости постоянной фазы: 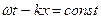. Положение этой плоскости определяется координатой x. 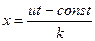. Скорость ее перемещения 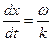совпадает со скоростью 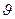распространения колебаний в среде. Таким образом 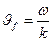(1) является скоростью волновой поверхности с заданной фазой и поэтому называется фазовой скоростью.

Реальные источники волн излучают не одну какую-либо монохроматическую волну, а совокупность волн, частоты которых находятся в пределах от ω до ω+ 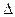ω, а волновые числа изменяются от k до k+ 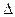k.

Так вот волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения max амплитуды волны, рассматривая тем самым max в качестве центра волнового пакета:

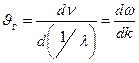
Возникает вопрос, какую из скоростей волны де Бройля (фазовую или групповую) следует сопоставить со скоростью микрочастицы в корпускулярном представлении. Для ответа на этот вопрос воспользуемся соотношением для фазовой скорости и подставив в него частоту и волновое число, найдём фазовую скорость волны де Бройля:.

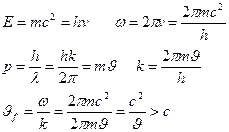
Оказывается, что она больше скорости света! Этот, на первый взгляд, парадоксальный, противоречащий теории относительности результат, в действительности не должен вызывать недоумения. Дело в том, что скорости предметов или передачи сигналов (энергии) не могут превышать скорости света. Между тем фазовая скорость как раз и не характеризует эти процессы.

Мы думаем, что групповая скорость может быть скоростью частицы. Чтобы двигаться дальше, нужно указать зависимость частоты ωот p и Е. Де-Бройль допустил, что зависимость 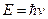, справедлива для фотонов, годится и для материальной частицы. Тогда:

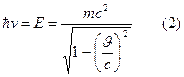
Наша групповая скорость:

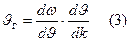
Подставим (2) –> (3), получим:

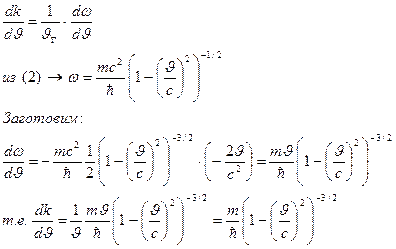
Интегрируем последнее выражение в предположении, что k=0, если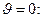

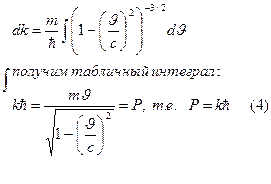
Это и предложил де Бройль. Мы пошли за ним и связали корпускулярную характеристику частицы P с волновой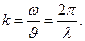

Следуя за гипотезой де-Бройля, мы пришли к гипотезе, что с движущейся частицей связана волна, характеризуемая волновым вектором k, который определяется импульсом частицы:

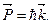
Таким образом длина волны, связанная с частицей, определяется выражением 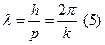. Это выражение известно под названием длины волны де Бройля для материальной частицы. Заметим еще раз здесь, что оно справедливо и для фотона.

Чтобы выяснить, как длина волны де-Бройля зависит от параметров движущейся частицы, запишем выражение (5) в виде:

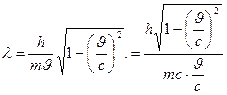
Мы видим, что с увеличением 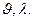уменьшается. При данной !

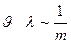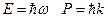– идеи де-Бройля, подтверждены впоследствии экспериментально.

Выясним, в какой степени идея де-Бройля о существовании волн у материальной частиц (т.е. и у материи) согласуется с опытом, т.е. убедится, что эта идея не противоречит установившемся понятиям макроскопической физике.

Рассмотрим частицу, которая мала с макроскопической точки зрения.

Пусть m=10^-5г. или m=10 мкг и она движется со скоростью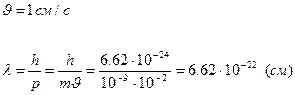

Это невероятно малая величина. Её малостью объясняется, что волны материи не проявляются в макроскопических явлениях, т.е. слишком малы, чтобы их можно было наблюдать. Как в оптике, чтобы проявились волновые свойства света, надо, чтобы какие-либо геометрические параметры прибора (например щель!) оказались сравнимыми с длиной волны света. Только в этом случае мы обнаружим отклонения от геометрической оптики в виде интерференции или дифракции.

Аналогично, чтобы обнаружить существование волн материи, мы должны иметь геометрический прибор, геометрические параметры которого сравнимы с длиной волны, т.е. какую-либо специальную решетку, с помощью которой можно было бы обнаружить дифракцию волн материи.

Волновые свойства в настоящее время наблюдается не только у элементарных частиц, но и у атомов и даже у небольших атомных кластеров. Австрийские ученые продемонстрировали волновые свойства молекулы фуллерена C(60), состоящей из 60 атомов углерода. Они показали, что с помощью пучка молекул С{60} можно создать интерференционную картину. Со временем создания квантовой механики идут дискуссии о том, в какой степени можно применять волновые кванто-механические представления к макроскопическим объектам. По видимому, вряд ли удастся обнаружить волновые свойства, например, у таких объектов, как вирусы. Молекула C{70} в данный момент является самым большим объектом, у которого наблюдается волновые свойства.

Скажем длина волны, равная 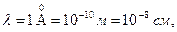если кинетическая энергия электрона равна 150,4 эВ – эта энергия полученная электроном, разогнанным разностью потенциалов в 100 В.

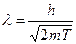
Такой же порядок величины имеет постоянная кристаллическая решетки. Таким образом, кристаллическая решетка вполне может служить

подходящей дифракционной решеткой для волн материи, что и использовали в своих опытах К.Дэвиссон и Л.Джермер и независимо У.Томсон (говорилось выше) и Тартаковский.

В опытах Дэвиссона и Джермера изучалось отражение электронов от поверхности монокристаллического никеля, а Томсон наблюдал прохождение электронов через тонкие кристаллические пленки (металл, фольгу). И в том и в другом случае были обнаружены дифракционные картины.

За свои исследования, блистательно подтвердившие представления квантовой механики, Дэвисон и Томсон были награждены в 1937 г. Нобелевской премией по физике. Однако их работы не просто подтвердили теоретические представления, а привели к созданию таких мощных и распространнёных методов исследования вещества, как дифракция медленных атомов и просвечивающая электронная микроскопия. В настоящее время дифракция электронов на кристаллической решетки является мощным инструментом изучения структуры твердого тела.