Временное преобразование; сжатие импульса

Рассмотрим явление сжатия импульса. Это явление — путь к получению импульсов предельно короткой длительности, приближающейся к длительности периода собственных колебаний световой волны. Однако, прежде чем приступить непосредственно к управлению длительностью лазерного импульса, имеет смысл сделать короткое отступление, чтобы напомнить такие понятия из электродинамики сплошных сред, как фазовая скорость, групповая скорость и дисперсия групповой скорости.

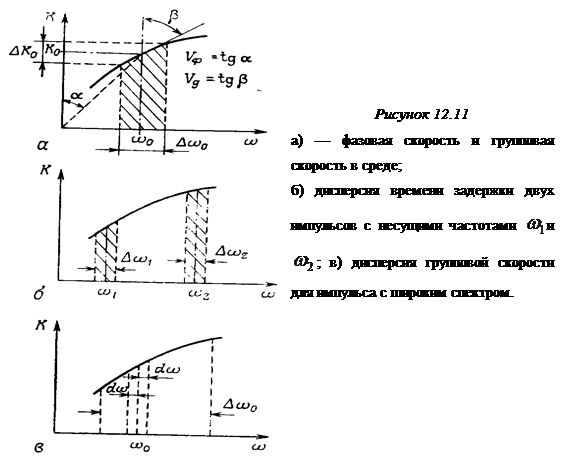
Рассмотрим среду, характеризующуюся конкретным дисперсионным уравнением, т.е. данным соотношением между волновым числом k и частотой 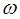(рисунок 12.11).

Электрическое поле плоской линейно поляризованной монохроматической электромагнитной волны с частотой 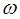будет распространяться вдоль оси z в соответствии с выражением Е ~ exp[i( 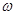t — kz)], где k = k( 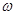) определяется дисперсионным уравнением среды. Поскольку фаза волны равна

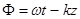, (12.40)

скорость данного фазового фронта будет такова, что элементарные изменения dt и dz временной и пространственной координат должны удовлетворять условию 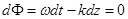. Отсюда следует, что фазовый фронт движется со скоростью

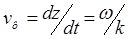(12.41)

которая называется фазовой скоростью волны.

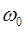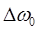Рассмотрим теперь световой импульс, распространяющийся в среде, и пусть и — центральная частота и ширина соответствующего спектра (рисунок 12.11,а). Предположим, что дисперсионное уравнение в пределах ширины линии 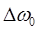может быть линеаризовано. Другими словами, запишем его следующим образом: 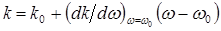где k_o — волновое число, соответствующее частоте 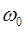. В этом случае, выполняя преобразование Фурье для электрического поля волны:

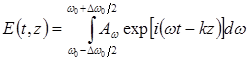, (12.42)

и подставляя приведенное выше линейное соотношение для k в зависимости от 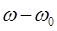, получаем

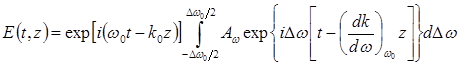(12.43)

где 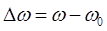. После интегрирования получается функция переменной 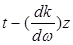. Тогда (12.43) можно представить в виде

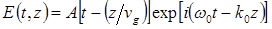(12.44)

где A — амплитуда волны или волнового пакета, 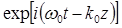— несущая волна, a v_g дается выражением

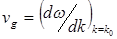(12.45)

Тот факт, что амплитуда волны является функцией переменной 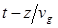, означает, что волновой пакет распространяется со скоростью v_g без изменения формы. Эта скорость называется групповой скоростью импульса, а ее величина в соответствии с (12.45) определяется наклоном кривой зависимости 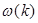в точке 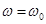. Из (12.44) видно, что несущая волна импульса распространяется со скоростью 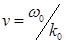, т. е. с фазовой скоростью непрерывной волны на частоте 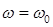. Важно отметить, что в общем случае дисперсионного уравнения, представленного на рисунке 12.11а, фазовая скорость несущей волны отличается, вообще говоря, от групповой скорости.

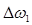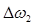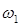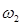Пусть теперь в среде распространяются два импульса, имеющих ширины спектральных линий соответственно и с центрами при и (рисунок 12.11б).

Если наклоны дисперсионной кривой на этих двух частотах имеют разные значения, то оба волновых пакета распространяются с различными групповыми скоростям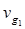и и 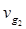. Таким образом, если максимумы обоих импульсов входят в среду одновременно, то после прохождения ими в среде расстояния L они становятся разделенными во времени на величину задержки

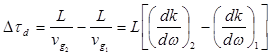(12.46)

Допуская, что дисперсионное уравнение в диапазоне частот 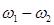можно аппроксимировать параболой, получим 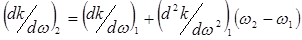и тогда величину 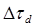можно записать в виде

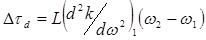(12.47)

Рассмотрим теперь случай, когда световой импульс имеет столь большую ширину линии 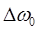, что дисперсионное уравнение не может допускать линейной аппроксимации (рисунок 12.11в).

В этом случае различные спектральные области импульса распространяются с различными групповыми скоростями, и, следовательно, форма импульса меняется во время распространения. Выбрав две соседние элементарные спектральные области импульса вблизи частоты 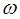, разделенные элементарным частотным интервалом 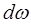, определим изменение временной задержки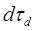

В соответствии с (12.47) имеем:

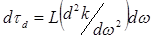(12.48)

Часто вводится в рассмотрение дисперсия групповой скорости (ДГС) в виде

ДГC = 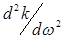(12.49)

Поскольку 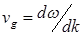, можно записать:

ДГС= 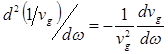(12.50)

Из (12.48) — (12.50) следует, что дисперсию временной задержки 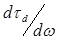можно представить в виде

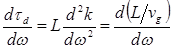(12.51)

Сделав эти предварительные замечания, можно перейти к рассмотрению метода сжатия сверхкоротких лазерных импульсов. Соответствующее устройство схематически представлено на рисунке 12.12.

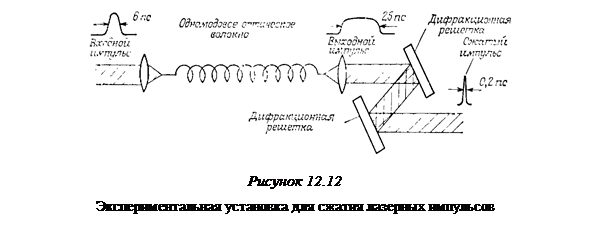Импульс лазера, работающего в режиме синхронизации мод, с относительно небольшой максимальной мощностью (например, Р_р = 2 кВт) и пикосекундной длительностью импульса (например, 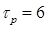пс) пропускается через одномодовое кварцевое оптическое волокно подходящей длины (например, L=3 м). Длина волны импульса (например, λ = 590 нм) попадает в область положительной дисперсии групповой скорости волокна (обычно λ < 1,3 мкм). Согласно (8.108), положительная дисперсия групповой скорости означает, что групповая скорость уменьшается с увеличением несущей частоты. После выхода из волокна импульс коллимируется и проходит через систему двух одинаковых дифракционных решеток, расположенных параллельно друг другу. Наклон этих решеток и расстояние между ними необходимо подобрать вполне определенным образом, описанным ниже. При выполнении этих определенных условий выходной пучок представляет собой импульс, длительность которого значительно меньше, чем у входного импульса (например, 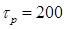фс). Таким образом, устройство, изображенное на рисунке 12.12, позволяет получить большой коэффициент сжатия (в нашем случае около 30).

Перейдем теперь к рассмотрению явлений, происходящих во время сжатия импульса [3].

Рассмотрим сначала процессы, которые имеют место при распространении импульса в оптическом волокне. При данном световедущем диаметре одномодового волокна (~ 4…5 мкм) импульс создает в сердцевине очень высокую интенсивность излучения. В этих условиях поле световой волны вызывает значительные изменения показателя преломления 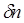материала волокна. Это изменение 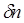пропорционально квадрату амплитуды поля импульса, так что мы можем записать 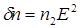, где для кварца .

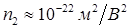Поскольку интенсивность I пропорциональна А², величину 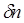можно записать в более общепринятом виде:

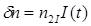(12.52)

где для плавленого кварца .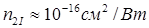

Заметим, что, поскольку здесь речь идет о коротком лазерном импульсе, интенсивность I является функцией времени. Это означает, что показатель преломления среды 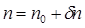(где n₀ — показатель преломления в отсутствие поля) также является функцией времени.

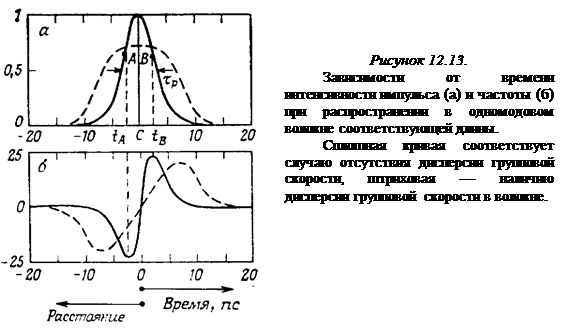Если потери в волокне малы, то импульс может сохранить высокую интенсивность на протяжении всего волокна, а это вызовет фазовую модуляцию несущей с достаточно большой глубиной. Предположим, что импульс на входе в волокно имеет колоколообразную форму (сплошная линия на рисунке 12.13а), и пусть этот импульс распространяется по бездисперсионному волокну на расстояние z.

В отсутствие дисперсии групповой скорости форма импульса не будет изменяться, и импульс, пройдя расстояние z по волокну, испытает сдвиг фазы 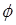,определяемый выражением

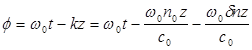(12.53)

где 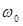— частота несущей входного импульса, а c₀ — скорость света в вакууме. Тогда мгновенное значение частоты светового импульса в точке с координатой z можно записать в виде

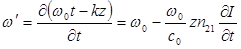(12.54)

Таким образом, мгновенное значение частоты несущей 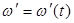линейно зависит от производной мгновенной интенсивности света по времени, взятой с обратным знаком. Следовательно, у импульса, показанного на рисунке 12.13а, несущая частота будет изменяться со временем так, как показано сплошной линией на рисунке 12.13б.

Заметим, что вблизи пика импульса, т. е. в той области, где временную зависимость можно описать параболой, мгновенное значение частоты несущей линейно растет со временем (т.е. говорят, что импульс обладает положительным смещением)[1]. Заметим также, что на крыльях импульса смещение частоты отрицательно, т. е. пр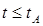и или 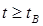на рисунке 12.13б.

Описанное явление носит название фазовой самомодуляции светового импульса.

Учтем теперь положительную дисперсию групповой скорости. Рассмотрим сначала форму невозмущенного светового импульса в данный момент времени как функцию координаты z. Поскольку интенсивность импульса зависит от z — v_gt, где v_g — групповая скорость, зависимость интенсивности импульса от переменной z та же, что и на рисунке 12.13, но при условии, изменения положительного направления оси на противоположное и умножения масштаба времени на v_g. Это означает, что некоторая точка А на рисунке 12.13а находится на переднем фронте, в то время как точка В — на заднем фронте. Заметим, что в соответствии с рисунком 12.13б несущая частота импульса 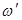вблизи точки А будет ниже, чем в точке С, где частота примерно равна 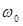. В то же время несущая частота импульса вблизи точки В будет выше, чем в С.

Поскольку волокно обладает положительной дисперсией групповой скорости, часть импульса вблизи точки А будет двигаться быстрее, чем часть импульса вблизи точки С, а последняя в свою очередь будет двигаться быстрее области вблизи точки В. Отсюда следует, что при распространении по волокну центральная часть импульса будет растягиваться.

При помощи тех же соображений можно показать, что фронты импульса будут не растягиваться, а обостряться, так как в этих областях смещение частоты отрицательно. Поэтому истинная форма импульса как функция времени в данной точке z будет такой, как показано на рисунке 12.13а штриховой кривой. Соответствующая зависимость смещения частоты показана штриховой кривой на рисунке 12.13б.

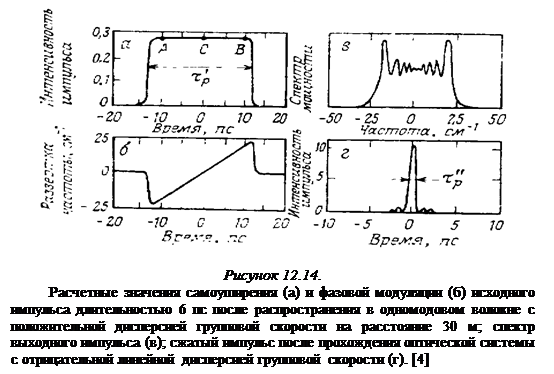Из рисунка 12.13а можно видеть, что из-за уширения, обусловленного дисперсией групповой скорости, пиковая интенсивность импульса, указанного штриховой кривой, меньше, чем для сплошной кривой. Кроме того, поскольку параболическая часть импульса распространяется теперь на более широкую область вблизи пика, положительное линейное смещение частоты распространяется на большую часть импульса. Установив эти общие особенности взаимодействия процессов фазовой самомодуляции и дисперсии групповой скорости, можно утверждать, что если длина волокна достаточно большая, то на выходе волокна форма импульса и смещение частоты будут изменяться во времени так, как изображено на рис. 12.14а и 12.14б.

Заметим, в частности, что положительное смещение частоты теперь линейно во времени на протяжении большей части импульса. Соответствующий спектр мощности этого импульса приведен на рис. 12.14в.

Благодаря фазовой самомодуляции ширина спектра (~ 50 см^-1) заметно превышает первоначальную ширину спектра импульса на входе в волокно (которая определялась обратной длительностью импульса, т. е. 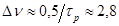см^-1 для рассмотренного случая 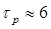пс.[2]

Отсюда следует, что ширина полосы на выходе в основном определяется фазовой модуляцией, а не длительностью огибающей.

Предположим теперь, что импульс на рисунке 12.14а (и 12.14б) пропускается через среду с отрицательной дисперсией групповой скорости. Рассуждая аналогично, придем к заключению, что область импульса вблизи точки А будет двигаться медленнее, чем вблизи точки С, а она, в свою очередь, будет двигаться медленнее области вблизи точки В. Отсюда следует, что импульс будет сжиматься.

Предположим теперь, что дисперсия групповой скорости среды, помимо того, что она отрицательна, не зависит от частоты. Тогда дисперсия временной задержки 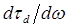будет также отрицательной и не будет зависеть от частоты, т. е. 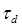линейно уменьшается с частотой. Поскольку смещение частоты импульса увеличивается линейно со временем (см. рисунок 12.14б), все точки импульса на рисунке 12.14а в случае, когда среда имеет соответствующую длину, сожмутся вместе в одно и то же время.

Эту длину можно определить с помощью соотношения [см. (12.103)]

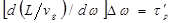(12.55)

где 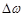— полное смещение частоты импульса (~ 50 см^-1 в примере, приведенном на рисунке 12.14б), а 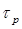— длительность импульса (~ 23 пс в примере на рисунке 12.14а). Заметим, что сжатие вместе всех точек импульса означает переход частотной модуляции импульса (показана на рисунке 12.14) в амплитудную модуляцию.

Поскольку в процессе этой операции спектр импульса сохраняется (т. е. он по-прежнему такой же, как на рисунке 12.14в), длительность сжатого импульса 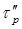должна быть приблизительно равна обратной ширине полосы спектра, т. е. 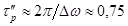пс. Так как первоначальная длительность импульса была равна 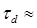6 пс (рисунок 12.12а), данный результат означает, что было достигнуто существенное сжатие импульса[3]

Следует заметить, что приведенное выше эвристическое рассмотрение основывалось на допущении, что импульс с частотным смещением может быть разделен на отдельные временные отрезки с различными частотами несущей. Хотя данная идея в принципе верна и позволяет дать простое описание явлений, более подробное рассмотрение этого подхода привело бы к некоторым концептуальным трудностям. Проведем поэтому более аккуратное рассмотрение с привлечением формализма Фурье.

Для получения сжатого импульса достаточно вычислить фурье-образы 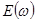импульсов, изображенных на рисунке 12.14а и 12.14б, и умножить их в частотной области на пропускание 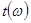среды с отрицательной дисперсией групповой скорости. При этом результирующий импульс получим вычислением обратного фурье-преобразования произведения .

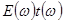Заметим, что в среде без потерь пропускание 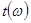представляет собой чисто фазовый член, определяемый выражением

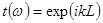, (12.56)

где L — длина среды, а величина 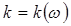определяется дисперсионным уравнением среды. Если среда имеет постоянную дисперсию групповой скорости, то 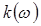можно разложить в ряд Тейлора относительно центральной частоты несущей 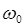с точностью до квадратичного члена:

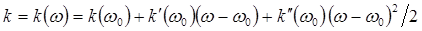(12.57)

где в соответствии с (12.45) и (12.49) имеем 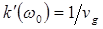и 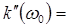ДГС. Подставляя данное разложение в (12.49) и производя обратное фурье-преобразование произведения 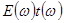, находим, что если вторая производная 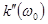отрицательна и удовлетворяет условию 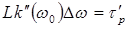, то мы имеем оптимальное сжатие импульса.

Оптимально сжатый импульс, вычисленный таким образом, показан на рисунке 12.14в. Длительность этого импульса имеет порядок 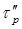= 0,6 пс, что указывает на сжатие исходного импульса длительностью 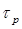= 6 пс примерно в 10 раз.

Одна из оптических систем, обеспечивающих отрицательную дисперсию групповой задержки 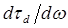, представляет собой пару параллельных одинаковых дифракционных решеток, изображенных на рисунке 12.15 [3].

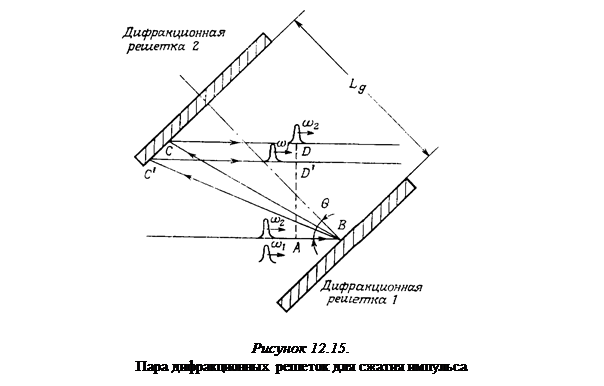Плоская волна, описываемая лучом АВ, падает на решетку 1 под углом 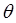к нормали решетки. Предположим, что падающая волна состоит из двух синхронных импульсов с частотам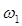и и 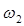, причем 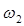> 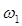. Вследствие дисперсии решетки импульсы проделают пути соответственно ABCD и . При этом задержка, которую испытывает импульс на частоте 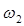, а именно 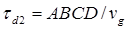, меньше задержки 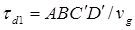на частоте 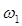. Поскольку 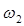> 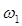, это означает, что дисперсия групповой задержки отрицательна. Дисперсионное уравнение при этом запишется в виде [3]:

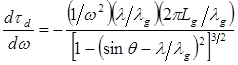(12.58)

где 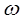— частота волны, λ— ее длина, λ_g— период решетки, а L_g — расстояние между решетками. Знак «минус» в правой части выражения (12.58) показывает, что дисперсия временной задержки действительно отрицательна. Величину дисперсии можно менять, изменяя L_g или угол падения θ.

Система, показанная на рисунке 12.12, применялась для осуществления сжатия импульсов при самых различных условиях. Например, импульсы длительностью около 50 фс на длине волны λ ≈ 620 нм от лазера на красителе с синхронизацией мод были сжаты с применением волокна длиной около 10 м до длительности около 6 фс. Эти импульсы состояли примерно из трех оптических периодов. Импульсы длительностью около 6 пс и пиковой мощностью около 2 кВт от лазера на красителе с синхронной накачкой и с синхронизацией мод были сжаты с помощью системы, показанной на рисунке 12.12, с использованием трехметрового волокна до длительности около 200 фс (Р_р = 20 кВт). Эти импульсы были повторно сжаты второй такой же системой с волокном длиной 55 см до длительности 90 фс [3].

Литература к лекции 12.

1. А.Л. Микаэлян, М.Л. Тер-Микаелян, Ю.Г.Турков. Оптические генераторы на твердом теле.

2. Н.В. Карлов. Лекции по квантовой электронике.

3. О. Звелто. Принципы лазеров.

4. К.И. Крылов, В.Т. Прокопенко, В.А. Тарлыков. Основы лазерной техники.

[1] Иногда говорят также «положительный чирп» (калька с английского “positive chirp”). Не будем пользоваться этим термином, так же, как и «свипированием частоты» (“frequency sweep”). Для них обоих существует вполне приемлемое слово «смещение», имеющее ясный физический смысл.— Прим. ред.

[2] Подчеркнем, что уширение спектра (т.е. появление в нем новых частот) обязано своим происхождением нелинейному эффекту зависимости показателя преломления от интенсивности. Никакой линейный процесс не может привести к генерации новых частот. — Прим. ред.

[3] Аналогичные методы получения укороченных импульсов путем создания вначале линейного частотного смещения с последующим сжатием импульса активно использовались в радиолокации после Второй мировой войны (радары с частотной модуляцией).