Самоограниченные переходы редкоземельных элементов.
| Ион | Tm3+ | Ho3+ | Er3+ |
| Длина волны, мкм | 2,01 | 2,12 | 2,78 / 2,94 |
| Лазерные уровни | 3H4 - 3H6 | 5I7 - 5I8 | 4I11 / 2 - 4I13/2 |
| Характерная глубина проникновения в воду, мкм |
Характерная глубина проникновения излучения данных типов лазеров в воду указана в связи с тем, что именно она главным образом определяет проникновение излучения в мягкие ткани организма, содержание воды в которых достигает 80%. Оценка глубины проникновения излучения в среду дается в предположении о справедливости закона Бугера. Это предположение достаточно хорошо выполняется при сильном поглощении, что имеет место в случае увеличения длины волны излучения свыше 1,4 мкм.
Концентрации примесных ионов для лазеров на самоограниченных переходах лежат в пределах от 10 до 40%. Это, как видим, много больше, чем для Nd+3. Оптимальная концентрация в каждом случае определяется структурой кристаллической матрицы (см. таблицу 10.1).
Разработка твердотельных лазеров на самоограниченных переходах ведется, начиная с 1974 г. Именно тогда впервые в ИОФАН СССР было предложено использовать для создания 3-микронного лазера кристаллы АИГ:Er при концентрации ионов Er3+>30%. Генерация была получена при комнатной температуре на длине волны 2,94 мкм.
На примере АИГ:Er-лазера, наиболее типичного для этих типов лазеров, можно проследить основные (экспериментально полученные) зависимости параметров выходного излучения от параметров активного элемента (энергии накачки, частоты следования импульсов, температуры, концентрации активных ионов). На основании этих зависимостей даже без проведения сложных расчетов можно заключить, что технологические факторы, влияющие на качество кристаллов, пространственную однородность примесей, оптические, термические и механические характеристики активных элементов, определяют на сегодня выходные характеристики в большей степени, чем принципиальные соображения, основанные на рассмотрении электрон-фононных и ион-ионных взаимодействий.
Отметим еще интересную особенность работы твердотельных лазеров в режиме свободной генерации, присущую как рассматриваемому типу, так и всем остальным. Речь идет о пичковой структуре импульса генерации. Это явление было впервые получено экспериментально и наблюдалось практически во всех твердотельных лазерах. Позднее пичковая структура наблюдалась и в прочих типах лазеров (газовых, жидкостных и др.). Типичная картина пичковой структуры показана на рисунке 10.6.

Рассмотрим упрощенную теоретическую модель твердотельного лазера, позволяющую объяснить появление пичковой структуры.
В силу предположения о начальной незаселенности обоих рабочих уровней будем считать, что инверсия n = n2 –n1 » n2 .
Кинетическое уравнение для числа фотонов N в моде резонатора:
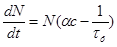 (10.19)
(10.19)
где α – показатель усиления среды, tф - время жизни фотона в моде.
Уточним физический смыслчленов, стоящих в правой части уравнения (10.19). Первый член описывает генерацию фотонов в моде. Он пропорционален инверсии населенностей через показатель усиления и скорости индуцированных переходовДля данного случая удобно переобозначить αc = nB (BN = Wi – вероятность индуцированных переходов), имея в виду, что мы будем совместно с уравнением для числа фотонов в моде (пропорционального интенсивности поля в резонаторе, а с ней – и выходной мощности) рассматривать кинетическое уравнение для инверсии населенностей. Второй член описывает убыль числа фотонов в соответствии с временем жизни фотона в моде. Здесь удобно ввести обозначение g = 1/tф. Величину g отождествим с радиационной шириной линии излучения лазера. Тогда уравнение (10.19) примет вид
 (10.20)
(10.20)
Соответственно уравнение для инверсии населенностей запишем в виде
 (10.21)
(10.21)
где обозначено:  — постоянная релаксации разности населенностей, L — скорость накачки. Физический смысл членов, входящих в уравнение (10.21), также прозрачен: инверсия обеспечивается за счет накачки L и убывает за счет индуцированных переходов NBn и всех остальных, в том числе спонтанных, Gn .
— постоянная релаксации разности населенностей, L — скорость накачки. Физический смысл членов, входящих в уравнение (10.21), также прозрачен: инверсия обеспечивается за счет накачки L и убывает за счет индуцированных переходов NBn и всех остальных, в том числе спонтанных, Gn .
Введенные константы g и G являются основными характеристиками взаимодействия поля в резонаторе с активной средой. Они имеют размерность частоты. Очевидно, что g, G « w0 (w0 – основная частота рабочего перехода). Релаксационные эффекты, описываемые g и G, и являются причиной возникновения пичковой структуры, т.е. временной модуляции интенсивности излучения. В самом деле, при стационарной генерации должно быть

При этом условии из уравнений (10.20) и (10.21) получаем стационарные значения инверсии и числа фотонов:
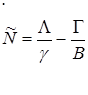 (10.22)
(10.22)
 (10.23)
(10.23)
Из (10.22) следует, что 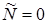 при
при  . Это условие естественно рассматривать как пороговое и ввести пороговую скорость накачки
. Это условие естественно рассматривать как пороговое и ввести пороговую скорость накачки  , а вместе с ней коэффициент превышения над порогом
, а вместе с ней коэффициент превышения над порогом
 (10.24)
(10.24)
Тогда выражение для стационарного числа фотонов запишется в виде
 (10.25)
(10.25)
Чтобы выяснить, что будет происходить при малых отклонениях N и n от стационарных значений, зададим эти величины в виде

 (10.26)
(10.26)
где 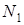 «
«  , n1 «
, n1 «  .
.
Подставляя (10.26) в кинетические уравнения (10.20) и (10.21) с учетом (10.22) и (10.23), получим для N1 и n1:
 (10.27)
(10.27)
 (10.28)
(10.28)
Продифференцируем (10.27). Вместо  при этом подставим правую часть (10.28) с учетом (10.23) и (10.26). Получим для N1 уравнение 2-го порядка:
при этом подставим правую часть (10.28) с учетом (10.23) и (10.26). Получим для N1 уравнение 2-го порядка:
 (10.29)
(10.29)
Введем сюда коэффициент превышения над порогом  . Получим окончательно
. Получим окончательно
 (10.30)
(10.30)
Это, как видим, уравнение колебательного типа с затуханием, решение которого N1 ~ ept дает для p:
p = - d ± iωm , где
 (10.31)
(10.31)
Если 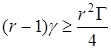 , то решение уравнения (10.30) имеет вид затухающей синусоиды с частотой ωm и скоростью затухания δ. Как ωm, так и δсущественно зависят от превышения r, т.е. от скорости накачки. Срыв колебательного режима затухания имеет место при
, то решение уравнения (10.30) имеет вид затухающей синусоиды с частотой ωm и скоростью затухания δ. Как ωm, так и δсущественно зависят от превышения r, т.е. от скорости накачки. Срыв колебательного режима затухания имеет место при  , т.е. затухание становится апериодическим.
, т.е. затухание становится апериодическим.
Как видно, наличие пичковой структуры определяется накачкой и соотношением между постоянными релаксации инверсии населенностей и числа фотонов в моде.
В твердотельных лазерах соотношение между γ и Γ может меняться в достаточно широких пределах. Если мы имеем дело с АИГ:Nd-лазером, то Γ/γ » 1, так что пичковый режим возможен только при больших превышениях. Правда, в этом случае и превышение может быть без особых затруднений сделано большим. Для самоограниченных лазеров Γ/γ ≤ 1, поэтому пичковый режим присутствует практически всегда. Если учесть при этом, что в случае самоограниченного перехода скорость накачки Λ также меняется во времени, то в правой части уравнения (10.30) появляется возмущение, результатом которого может стать превращение затухающих релаксационных колебаний в незатухающие. Это также наблюдается на опыте. Типичные значения для периодов пичковых структур (следования пичков) составляют 0,1…10 мкс.
Изложенные обстоятельства позволяют считать, что возможности совершенствования конструкции твердотельных лазеров далеко не исчерпаны. Соответственно и перспективы применения их в медицине реализованы пока в очень малой степени. Однако конкуренция со стороны волоконных лазеров (см. Л9) может привести к тому, что эти перспективы так и останутся нереализованными.
В заключение приведем таблицу с техническими характеристиками некоторых медицинских установок (лазерных перфораторов) на базе АИГ:Er-лазеров.
Таблица 10.3.
Дата добавления: 2017-01-26; просмотров: 1621;











