ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ.

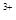Лазер на кристалле АИГ:Nd, нашедший широкое применение в медицине, является типичным твердотельным лазером на примесном кристалле. Активная среда этого лазера — кристалл Y₃Al₅O₁₂ (иттрий-алюминиевого граната), активированный ионами неодима Nd . Ионы неодима, занимая место основного иона решетки, подвергаются действию внутрикристаллического поля. В результате этого взаимодействия уровни иона Nd 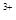расщепляются и образуют интересующую нас схему рабочих уровней, на которых достигается инверсия (рисунок 10.1.)

	Рис. 10.1. Схема возбуждения уровней Nd в кристалле Y3Al5O12.

Накачка производится оптическим способом, путем освещения кристалла интенсивным широкополосным излучением специальной лампы. Благодаря наличию широких полос поглощения кристалла (подобно зонам в полупроводнике, только без свободных носителей заряда), энергия которых близка к уровням иона Nd 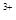посредством массированного заселения метастабильного 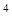F3/2 уровня с временем жизни ~ 0.2 мс обеспечивается инверсия по отношению к нижележащим уровням 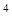I (см. рис. 9.1.). Наибольшей вероятностью обладает переход 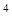F_3/2 ® 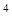I_11/2 (l=1.064мкм). Этот переход обладает весьма высокой квантовой эффективностью (уровень 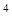I_11/2 отстоит от основного 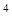I_9/2 состояния всего на ~ 0.25 эВ, тогда как рабочий переход составляет ~ 1.16 эВ — почти в 5 раз больше). Общая квантовая эффективность определяется близостью полос поглощения к верхнему уровню 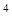F_3/2. В кристаллах алюмоиттриевого граната (АИГ) имеется интенсивная красная полоса поглощения (энергия возбуждения ~ 1.9 эВ). В результате квантовая эффективность составляет ~ 60% и уступает только полупроводниковым лазерам.

Энергосъем с единицы объема активной среды АИГ:Nd -лазера определяется степенью активации кристалла ионами Nd 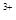. Обычно оптимальная концентрация ионов Nd 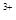составляет ~0,5…1,5%, при бόльших концентрациях резко падает эффективность накачки. Выходная мощность определяется размерами активного элемента, выполняемого в виде цилиндрического стержня длиной до 250 мм и диаметром до 15 мм. Впрочем, такие большие кристаллы вырастить трудно (требования к пространственной однородности и постоянству оптических сред высоки), поэтому в промышленно выпускаемых лазерах обычно длина кристалла не превышает 120 мм, а диаметр — 6 мм. В непрерывном режиме выходная мощность АИГ:Nd-лазерах достигает 1 кВт, в импульсном реализованы все варианты как моноимпульсного, так и импульсно-периодического типа с длительностями импульсов до 10 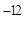с.

Исключительно широкое распространение этого типа лазеров обусловлено рядом преимуществ над другими типами (прежде всего газовыми) с технологической точки зрения. Прежде всего — это отсутствие вакуумных объемов, приводящих к неизбежному накоплению ненужных компонент в активной среде и, в конечном счете, — прекращению ее функционирования как активной среды. Степень надежности и долговечности кристалла в штатном режиме работы несравненно выше, чем газонаполненных трубок. Кристалл имеет по сравнению с газоразрядной трубкой несравненно меньшие размеры и, как правило, изготавливается в конструктивном объединении с лампами накачки (квантрон). Поскольку лампы накачки имеют примерно такие же размеры, как и кристалл, для их питания не требуется высоких напряжений, что, в свою очередь, упрощает конструкцию блока питания. К системе охлаждения в данном случае предъявляются примерно такие же требования, как и для мощных газовых лазеров (двухконтурная с замкнутым внутренним и открытым внешним контурами), но широкие возможности по части выбора режима генерации позволяют сплошь и рядом упрощать систему охлаждения вплоть до полного отказа от воды.

Мы несколько отступили от традиционной методики ознакомления с твердотельными лазерами, где обычно начинают с лазера на рубине как первого в истории лазера. На сегодня лазер на рубине уже утратил свое первостепенное значение и из медицины вытеснен гранатовыми и другими твердотельными лазерами почти полностью. Все же, отдавая дань легендарному прошлому рубинового лазера и учитывая его огромную роль в развитии квантовой электроники и нелинейной оптики, рассмотрим коротко его работу.

Рубин — это твердый раствор Al₂O₃:Cr₂O₃, т.е. в кристаллическую структуру корунда Al₂O₃ внедрены ионы хрома Cr . Подобно случаю граната с неодимом, термы Cr испытывают расщепление в сильном поле кристаллической решетки корунда. Образуется структура уровней иона хрома (см. рисунок 10.2).

Широкие полосы поглощения на F-линиях 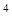F₁ и 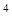F₂, образовавшихся ввиду расщепления вырожденных уровней свободного иона Cr , соседствуют с узкими линиями F₂ и Е₁, последняя из которых, в свою очередь, расщепляется на два уровня, разделенных узкой щелью (29 см ). По мере возрастания волнового числа линии переходов обозначены буквами R,U,B,Y ( от английского RUBY — рубин). Полосы 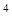F₁ и 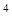F₂ сильно поглощают излучение лампы накачки (показатель поглощения 2–3 см ). При прохождении импульса накачки энергия безызлучательным образом перекачивается из полос 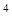F₁ и 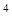F₂ в дублет Е с характерным временем релаксации ~ 100 нс. Дублет Е образует верхний рабочий уровень энергии, основное состояние — нижний. Генерация происходит на обеих R-линиях, но более интенсивной является нижняя ( = 694,3 нм). Особенностью рубинового лазера является, как видно, трехуровневая схема возбуждения (в отличие от четырехуровневой, характерной для большинства рассмотренных выше лазеров, см. Л2, Л3).

Поскольку в данной трехуровневой схеме инверсия возникает по отношению к основному состоянию, возникает она не сразу после включения накачки. Частицы (ионы хрома) должны накопиться на метастабильном уровне Е под действием накачки в течение некоторого конечного времени t. Уровни 1 (основное состояние) и 2 (полоса поглощения при накачке) связаны излучением накачки, индуцирующим переходы 1 2 с вероятностью W (см. рисунок 10.3).

Распад верхнего уровня происходит по каналам 2 1 и 2 3 с вероятностями w₂₁ и w₂₃. Уровень 3 распадается с вероятностью w₃₁. Термическим заселением уровней 2 и 3 пренебрегаем. Записав скоростные уравнения для населенностей уровней 1, 2, 3:

(10.1)

где — плотность активных частиц, в стационарном состоянии (все производные равны 0), получим для разности населенностей n₃ — n₁:

(10.2)

Очевидно, n3>n1 при условии:

(10.3)

т.е. при w₂₃ > w₃₁ , что имеет весьма простой смысл: верхний уровень должен населяться быстрее, чем опустошаться. Для рубина выполнены неравенства w₂₃ >> w₃₁ , w₂₃>> w₂₁, и условие (10.3) принимает вид:

W > w₃₁ (10.4)

Одновременно при всех при всех разумных интенсивностях накачки:

W < w₂₃ (10.5)

Поэтому на резонансном уровне 2 частицы не накапливаются. Полагая n2 = 0, сведем систему (10.1) к одному уравнению ( ):

(10.6)

Для инверсии x = n3 – n1 имеем :

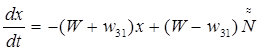(10.7)

Это уравнение при начальном условии x( 0 ) = –N имеет решение:

(10.8)

Полагая, что накачка W включается в момент t=0 и в дальнейшем остается неизменной, можно найти «время просветления» рабочего перехода из условия x( ) = 0:

(10.9)

Произведение W , определяющее минимальную энергию, необходимую для приведения системы из поглощающего состояния в усиливающее, равно:

(10.10)

и при W >> w₃₁ стремится к постоянной величине:

Е ~ ln2 (10.11)

Последнее выражение имеет следующий смысл: при больших интенсивностях произведение W пропорционально энергии, необходимой для перевода всех частиц из основного состояния на верхний лазерный уровень. Поскольку инверсия создается по отношению к заселенному основному состоянию, необходимо, «загнать» на уровень 3 через уровень 2 не менее половины всех частиц. Поэтому лазер, работающий по трехуровневой схеме, очень трудно заставить работать в непрерывном режиме.

Сопоставляя с четырехуровневой схемой АИГ:Nd-лазера, где нижний лазерный уровень отделен от основного состояния и в принципе может быть не заселен, видим, что последний вариант значительно предпочтительнее в плане снижения пороговой плотности накачки. В самом деле, запишем систему скоростных уравнений для четырехуровневой схемы аналогично (10.1) (см. рисунок 10.4), следуя методике лекции 3:

(10.12)

Стационарная инверсия на переходе 3 4 x = n3 – n4 положительна при условии:

(10.13)

Условие (10.13) принципиально отличается от (10.3) тем, что оно не зависит от накачки W. Если учесть при этом, что обычно w₂₃ >> w₂₄, w₃₄ , w₃₁, то (10.13) принимает совсем простой вид:

w₄₁ > w₃₄ (10.14)

откуда следует, что нижний лазерный уровень должен быстрее распадаться, чем заселяться переходами с верхнего лазерного уровня. Заметим, что во всех рассмотренных типах лазеров, кроме, конечно, рубинового, расселение нижнего лазерного уровня представляет одну из главных забот.

Конечно, условие (10.14), означающее отсутствие порога генерации в четырехуровневой схеме, является идеализированным. Дело в том, что в системе (10.12) мы пренебрегли вероятностью безызлучательного заселения нижнего уровня из основного состояния w₁₄. Но это заселение, вообще говоря, всегда имеет место из-за тепловых эффектов. Значит, условием малого порога генерации в четырехуровневой системе можно считать:

E >> k_б Т (10.15)

где E — разница энергий основного и нижнего рабочих уровней. Из (10.15) следует, что нагрев активной среды может «испортить» четырехуровневую схему, сведя ее к трехуровневой и тем самым резко «задрав» порог генерации в импульсном режиме и вообще уничтожив возможность генерации в непрерывном режиме. Вообще при приближении k_бТ к E всегда обнаруживается сильная температурная зависимость порога генерации, ввиду чего охлаждение кристалла (и вообще любой активной среды) является принципиально важным обстоятельством, а не просто некоторым улучшением эксплутационных характеристик.

Лазеры на АИГ:Nd и рубине дают вполне наглядное представление о твердотельных лазерах, но ни в коем случае не следует забывать об исключительном разнообразии твердотельных активных сред. Например, тот же кристалл граната может быть активирован не неодимом, а другими редкоземельными элементами. Это представляет возможность выбора длин волн излучения, представляющих специальный интерес для медицины. Так, для хирургии такими длинами волн являются > 1200 нм, попадающие в область сильного поглощения водой (основной составляющей мягких тканей). С этой точки зрения интересны лазеры на ионах Ho ( = 2060 нм) и Er ( = 2940 нм). Кроме того, возможно использование других кристаллов (в настоящее время известно более 300 кристаллов, используемых для активирования генерирующими ионами). Тем не менее, наиболее употребительны для медицинских целей все-таки кристаллы со структурой граната, поскольку они наиболее освоены технологически и обладают всем необходимым набором свойств.

Совершенствование твердотельных лазеров идет в настоящее время по пути повышения энергоотдачи кристаллических структур, достигаемого путем введения в матрицу кристалла дополнительных примесей, поглощающих неиспользованную часть энергии накачки и передающих ее активным центрам. Такую роль играют, например, ионы хрома в гадолиний-скандий-иттриевом гранате (ГСГГ), позволяя поднять в несколько раз (!) КПД по сравнению с АИГ. Лазер на ГСГГ с Nd позволяет реализовать КПД до 10%, что открывает новые возможности в части конструирования мощных малогабаритных и экономичных лазеров. Поскольку на сегодня пока не получены столь же мощные импульсы излучения Ho и Er-лазеров, как для случая Nd, предпринимаются значительные усилия для повышения концентрации ионов Ho и Er в кристаллах гранатов. На этом следует остановиться подробнее.

Мы подчеркивали достоинства лазера на АИГ:Nd, позволяющих получать генерацию в практически любом режиме, какой только может быть востребован. Ситуация в кристалле граната, активированном ионами Nd⁺³ , вроде бы близка к идеальной. В самом деле, верхний рабочий уровень ⁴F_3/2 является метастабильным, т.е. имеет время жизни порядка 0,2 мс. Любой из нижних рабочих уровней (⁴I_15/2, ⁴I_13/2, ⁴I_11/2 )― короткоживущий, т.е. условия для создания инверсии при наличии подходящих полос поглощения кристаллической матрицы граната предельно благоприятны. Время многофононной релаксации (т.е. безызлучательного распада за счет взаимодействия с кристаллической матрицей) состояния ⁴F_3/2 много больше, чем его радиационное время жизни. В результате квантовый выход люминесценции верхнего лазерного уровня, определяющий возможность преобразования энергии возбуждения кристаллической матрицы в лазерное излучение, близок к 100%. Интенсивная красная линия поглощения кристалла граната обеспечивает эффективную перекачку энергии из полосы поглощения на верхний лазерный уровень. Это активно используется при накачке узкополосными источниками света (светодиодами). В общем, все мыслимые достоинства, необходимые для создания инверсии, налицо. Почему же этот тип лазера все-таки нас не совсем удовлетворяет?

А вот оказывается, что слишком хорошо ― это тоже нехорошо. Ионы Nd⁺³ при накачке практически все оказываются в возбужденном состоянии. При этом возрастает роль процессов переноса энергии от иона к иону, так что механизмы релаксации становятся коллективными. Это ограничивает, причем существенно, предельную концентрацию активирующей примеси Nd⁺³. В самом деле, вероятность передачи энергии от одного иона к другому определяется формулой

(10.16)

где С ― константа скорости переноса энергии от иона к иону, определяемая перекрытием спектров этих частиц и матричными элементами операторов их резонансных переходов. Величина С может быть с необходимой точностью получена квантовомеханически в первом порядке теории возмущений (диполь-дипольное взаимодействие), но может быть вычислена и с помощью классической модели связанных осцилляторов. Последнее оказывается возможным по той причине, что в окончательное выражение для С, вычисляемой по теории возмущений, не входит постоянная Планка:

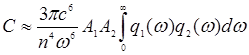(10.17)

Здесь с — скорость света, А₁, А₂ — коэффициенты Эйнштейна для спонтанных переходов на частоте w из рассматриваемых состояний 1 и 2 для взаимодействующих диполей, n — показатель преломления среды ( для кристалла можно считать n² = e, где e — диэлектрическая проницаемость), q₁(w) и q₂(w) — форм-факторы линий q₁(w) и q₂(w), дающие распределение осциллирующих диполей по частотам, или вероятность обнаружения осциллятора 1 или 2 на частоте w. Вычисление константы скорости переноса энергии во многом аналогично вычислению ширины линии рабочего перехода (см. Л4). Интеграл называется, как известно, интегралом перекрытия. Коэффициенты Эйнштейна характеризуют способность возбужденных ионов к взаимодействию, перекрытие спектров обеспечивает возможность этого взаимодействия. Электростатический характер взаимодействия осциллирующих диполей выражается в сильной (~ R⁶) зависимости вероятности переноса от расстояния между ними. Но среднее расстояние между ионами связано с их концентрацией: , где N — плотность ионов. Тем самым вероятность переноса энергии определяется как константой скорости, так и концентрацией ионов. Конкретный вид функции = (C,N) в зависимости от выбора кристаллической матрицы и активирующей примеси может достаточно сильно меняться, но из приведенных оценочных рассуждений очевидно, что возрастает с ростом C и N. Для Nd⁺³ константа С по сравнению с другими редкоземельными элементами весьма велика, поэтому большую концентрацию Nd⁺³ допустить нельзя. Можно слегка смягчить ситуацию добавкой вспомогательной примеси, уменьшающей интегралы перекрытия, и тем самым повысить концентрацию ионов Nd⁺³ примерно до 10²¹ см^-3, что составляет уже не доли процента, а проценты. Но за это приходится платить уменьшением эффективности перекачки энергии возбуждения не верхний рабочий уровень, так что удельный энергосъем лазера на переходах иона Nd⁺³ в итоге не увеличивается.

Чисто медицинский аспект добавляет «головной боли» по поводу неодимового лазера: его характерные длины волн 1,064 мкм, 1,32 мкм, 1,44 мкм попадают в область относительно большой прозрачности мягких тканей, в результате АИГ:Nd-лазер при всех его достоинствах имеет весьма ограниченное применение в хирургии (см. Л1).

Отметим глубокую аналогию, существующую между релаксационными процессами в твердом теле (электрон-фононное и диполь-дипольное взаимодействие, часто называемое кросс-релаксацией) и столкновительной релаксацией в газах (см. Л4). Учет изложенных обстоятельств и привел к большому разнообразию используемых в твердотельных лазерах кристаллических матриц (более 300). Наиболее часто используемые кристаллы приведены в таблице 10.1.

Таблица 10.1.