Диаграмма устойчивости резонаторов.

Для рассмотрения характеристик резонаторов с различной геометрией удобно воспользоваться параметрами g_i=1-L/R_i, где i=1,2 (см. рисунок 7.2)

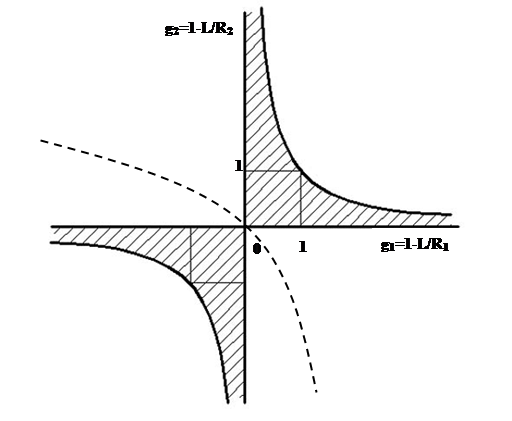
Рисунок 7.2. Диаграмма устойчивости резонаторов.

В плоскости g_iобласти, в которых выполняются неравенства, обратные (7.5), ограничены осями координат и гиперболой g₁g₂=1 и называются областями устойчивости оптических резонаторов. На рисунке 7.2 эти области заштрихованы.

Обратимся к конкретным случаям геометрии резонаторов, характеризующихся определенными точками на диаграмме устойчивости.

Конфокальный резонатор, (g₁=0,g₂=0) расположен на границе устойчивости (рисунок 7.3).

Малейшая асимметрия выводит резонатор в область неустойчивости.

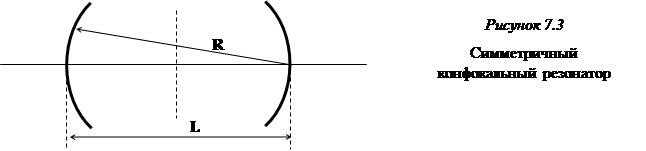Полуконфокальный резонаторL=R₁/2, R₂=∞ (g₁=0,5,g₂=1), который должен иметь с точки зрения поперечного распределения такие же характеристики, как симметричный конфокальный, оказывается в устойчивой области (рисунок 7.4).

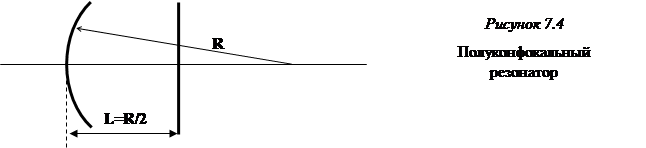
Физически это можно истолковать так, что сферическое зеркало, «смотрясь» в плоское, «видит само себя». Плоское зеркало располагается как раз в перетяжке гауссова пучка (мы помним, что в перетяжке фронт плоский). Такая конфигурация зеркал удобна, во-первых, для реализации наименьшего размера пучка на выходе лазера (плоское зеркало делают выходным, сферическое – глухим), во-вторых, для удобства определения размера перетяжки по пятну на выходном зеркале. Поэтому полуконфокальный резонатор нашел весьма широкое практическое применение.

Плоскопараллельный резонатор, или резонатор Фабри-Перо(g_{2 =} 1, g₂ = 1)также попадает на границу устойчивости, что также физически ясно ― малейшее отклонение распространения волны от направления, перпендикулярного плоскости зеркал, приводит к быстрому выходу волны из резонатора.

Симметричный концентрический резонатор L=2R₁ =2R₂(g_{2 =} -1, g₂ = -1), в котором совпадают центры кривизны зеркал, снова попадает на границу ус
тойчивости (рисунок 7.5), так же, как и полуконцентрический резонатор L=R₁, R₂=∞ (g₁=0,g₂=1).

Концентрический резонатор имеет наибольшую возможную при заданных радиусах кривизны зеркал длину. Несмотря на то, что такая конфигурация кажется на первый взгляд далекой от оптимальной, она нашла довольно частое практическое применение.

В самом деле, увеличение угла расходимости пучка не является однозначно отрицательным явлением, поскольку одновременно улучшает условия селекции мод. Используя аналогию с угловой дисперсией спектральных приборов, можно с успехом выделять как основную моду, имеющую минимальный поперечник на выходном зеркале, так и, в случае необходимости, моды более высоких порядков. С другой стороны, увеличение длины резонатора позволяет, вообще говоря, использовать и бόльшую длину активного элемента, следовательно, получать выигрыш в выходной мощности. Таким образом, конфигурации резонаторов, близкие к полуконцентрической, часто используются в лазерах, особенно в тех случаях, когда требуется получить повышенное сосредоточение выходной мощности в одной моде.