Элементы интерпретации данных гравиразведки.
Эти карты далее подвергаются интерпретации, задачей которой является получение сведений об источниках выявленных аномалий, форме и глубине залегания границ раздела пород с разной плотностью и установление связи этих границ с геологическими границами. Более подробно об интерпретации написано в нашем пособии [6]. Особенность интерпретации гравиметрических (как, впрочем, и магнитометрических) данных состоит в том, что гравитационное (и магнитное) поле является по своей природе суммарным, интегральным. Оно сформировано влиянием всех неоднородностей разреза, вносящих в него свой вклад, пропорциональный массе неоднородности и обратно пропорциональный квадрату ее удаления от измерительного прибора на поверхности наблюдений. То есть механизм гравитационного действия объясняется, как уже говорилось, исходящим из закона тяготения Ньютона соотношением m/r2, где r – упомянутое удаление, а m – масса, то есть произведение объема неоднородности на ее избыточную (эффективную) плотность. Избыточная плотность – это разность плотностей тела - источника аномалии и пород, вмещающих это тело (неоднородность). Причем все эти плотностные неоднородности разреза действуют единовременно. Вклад ближайшей из них может оказаться наиболее значительным, поскольку она ближе к поверхности наблюдений. Но если, допустим, какая-то из масс отличается существенно большей контрастностью, то может оказаться, что более удаленное тело также иди даже весомее участвует в натяжении пружины прибора. В итоге на суммарной кривой Δg, зарегистрированной при перемещении прибора вдоль профиля, уровень значений поля на отдельных максимумах может оказаться и очень близким, и весьма различным. А может получиться и так, что на суммарной кривой окажется, к примеру, меньше экстремумов, чем неоднородностей в разрезе, особенно если какие-то из них располагаются поблизости друг от друга и их влияние на суммарной кривой сольются в единый максимум ( как было показано на рис.3) или минимум (в случае, когда вмещающие породы имеют бóльшую плотность). В то же время в результате интерпретации необходимо выявить все реально существующие в разрезе гравиактивные тела и охарактеризовать их свойства порознь, а не вместе.
Сказанное дает возможность уяснить, что первой интерпретационной задачей в гравиразведке (и в магниторазведке) является разделение аномалий. И только после того, как удастся от суммарного поля перейти к изолированным аномалиям, можно будет заняться уточнением геологической природы этих аномалий и, наконец, определением геометрических и собственно, геологических, характеристик их источников. Итак, необходимо в соотношении
ΔgаБ = Δ1gа + Δ2gа +….. + Δngа
определить отдельные составляющие Δ1gа, Δ2gа и т.д.
Задача разделения аномалий может быть решена разными путями. Самым популярным и часто востребуемым способом являются так называемые частотные трансформации, то есть преобразования, основанные на различии аномалий по частоте или по размерам. Аномалии принято классифицировать на региональные (низкочастотные, большие по размерам) и локальные, (высокочастотные, небольшие). Например, на рис. 13 показаны две аномалии (максимума) одинаковой интенсивности.

Рис.13. Локальная (1) и региональная (2) аномалии.
Однако первая из них – узкая, пиковая, а вторая широкая, плавная. Первую можно отнести к локальным, а вторую к региональным. Очевидно, что на карте аномалий силы тяжести они будут локализованы различным образом. Локальные аномалии создают высоковозмущенные поля с близко расположенными изолиниями Δg, а региональные, занимающие значительные пространства, образуют более спокойные поля со значительными интервалами между изолиниями. В параграфе, повествующем о геологической природе аномалий ΔgБ, среди выделенных факторов такие как рельеф поверхности фундамента или глубинный фактор обычно формируют региональную составляющую поля, а структура осадочного чехла локальную. Из приведенного рисунка хорошо видно, что источником пиковой аномалии скорее всего может служить небольшое, но неглубоко залегающее геологическое тело, тогда как аномалию 2 можно объяснить влиянием крупной, но относительно глубоко погруженной неоднородности. Такого рода различия как раз и позволяют эффективно использовать частотные преобразования. К ним относятся такие способы как осреднение поля в скользящем окне с последующим вычитанием осредненного поля из суммарного поля Буге (в ходе обучения студенту будет предложена лабораторная работа, реализующая этот способ).
Используются и другие реализации идеи частотного разделения: способ аналитического продолжения поля в нижнее полупространство, тренд-анализ и др., о которых можно прочитать в учебниках и справочниках по гравиразведке. Проиллюстрировать результаты осреднения поля с последующим вычитанием Δgср из исходного нетрансформированного поля можно примером на рис.14.
 |  |
|
|
Рис. 14. Пример локализации аномалий поля силы тяжести
а) - исходная карта аномального поля силы тяжести Δg фрагмента территории Астраханского свода ; б) карта, преобразованная по методу осреднения.
После получения изолированной аномалии можно переходить собственно к ее интерпретации, используя модельный подход, идея которого излагалась в тексте лекции 2. Она состоит в решении прямых и обратных задач. Вначале попробуем осуществить решение прямой задачи гравиразведки в общем виде.
 Допустим, что источником изолированной аномалии является некое неоднородное (то есть с меняющейся плотностью) геологическое тело произвольной формы, расположенное под поверхностью наблюдений во вмещающей среде с плотностью σ0. Поверхность наблюдения можно аппроксимировать плоскостью XOY. Решение прямой задачи должно дать ответ на вопрос: каково значение g в произвольной точке N на плоскости XOY, если известны (заданы) геометрические и петрофизические характеристики тела источника. Расположим наше тело в трехмерной системе координат XOY так, чтобы через него проходила ось z, перпендикулярная поверхности наблюдений, как это показано на рис.15.
Допустим, что источником изолированной аномалии является некое неоднородное (то есть с меняющейся плотностью) геологическое тело произвольной формы, расположенное под поверхностью наблюдений во вмещающей среде с плотностью σ0. Поверхность наблюдения можно аппроксимировать плоскостью XOY. Решение прямой задачи должно дать ответ на вопрос: каково значение g в произвольной точке N на плоскости XOY, если известны (заданы) геометрические и петрофизические характеристики тела источника. Расположим наше тело в трехмерной системе координат XOY так, чтобы через него проходила ось z, перпендикулярная поверхности наблюдений, как это показано на рис.15.

Рис.15. К решению прямой задачи гравиразведки в общем виде.
Для того, чтобы определить, чему равно значение gz в точке N необходимо, принимая во внимание то обстоятельство, что тело М неоднородно по плотности, использовать аппарат разбиения этого тела на бесконечно малые фрагменты, в пределах каждого из которых можно признать плотность постоянной. Тогда можно будет посчитать гравиэффекты таких фрагментов в точке N, а затем все эти эффекты просуммировать, то есть проинтегрировать по всему объему тела. Иными словами, необходимо осуществить вначале дифференцирование, а затем интегрирование. При этом надо учесть, что сила притяжения – вектор. Поскольку направление силы притяжения каждым отдельным фрагментом будет отличаться от прочих, простое суммирование в такой ситуации не проходит, поэтому придется складывать составляющие (проекции) векторов на ось Z. Иными словами, гравиэффект каждого малого фрагмента можно оценить, следуя закону тяготения, следующим образом:
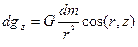
Здесь 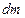 - элемент массы М, G – гравитационная постоянная, r – расстояние между
- элемент массы М, G – гравитационная постоянная, r – расстояние между 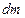 и точкой N на поверхности наблюдения (где как бы находится единичная масса прибора – гравиметра, испытывающая притяжение со стороны
и точкой N на поверхности наблюдения (где как бы находится единичная масса прибора – гравиметра, испытывающая притяжение со стороны 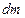 .
.
Умножением 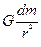 на
на  удается получить проекцию силы притяжения, направленной по r на ось Z.
удается получить проекцию силы притяжения, направленной по r на ось Z.
Значение r можно определить, вспомнив из аналитической геометрии, чему равняется расстояние между двумя точками в трехмерном пространстве. Если обозначить эти координаты для N через x, y и z (причем, поскольку точка N принадлежит к поверхности, ее координата z = 0), а для dm( 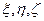 ), то в соответствии с этой формулой
), то в соответствии с этой формулой
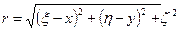
Поскольку косинус есть отношение гипотенузы к прилежащему катету, то есть r/z, выражение для dgz можно переписать в виде dgz= G 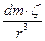 , или
, или
dgz= Gdm 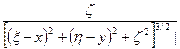 .
.
Чтобы оценить гравиэффект gz, создаваемый всей массой М необходимо проинтегрировать приведенное выражение по всему замкнутому контуру М, то есть по всему объему тела – источника, иными словами, взять тройной интеграл по X, Y и Z, причем константу G можно вынести за знак интеграла
gz= G 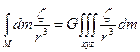
Это выражение и будет представлять собой решение прямой задачи гравиразведки в общем виде.
Теоретически, этот интеграл можно вычислить («взять») только для тел простой геометрической формы. Поэтому значительную часть объема интерпретационного раздела в учебниках по гравиразведке составляет подробное аналитическое решение прямой (и обратной) задачи для таких тел: шара, цилиндра, куба, уступа и пр. Предполагается, что такими телами можно аппроксимировать, то есть упрощенно описать, реальные природные объекты. Например, изометричный по плановым очертаниям соляной купол, или антиклинальную складку можно достаточно успешно аппроксимировать шаром. Рассмотрим самый простой двумерный плоский случай решения прямой задачи для такого однородного шара.

Рис.16. Аномалия над шаром.
Пусть этот шар ( рис.16 ) располагается так, что ось Z проходит через его центр, а точка наблюдения находится на оси X, то есть координаты центра 0 – (0,0,z), а точки наблюдения N – (x,0,0)
Тогда, исходя из выражения для gz, полученного ранее (в общем виде) можно записать, что
gz=G 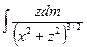
Это очевидно, поскольку r= 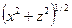
Полученное выражение можно привести к более простому виду, поскольку из приведенного рисунка следует, что на аномалию влияют лишь избыточная масса (а не размеры) шара и положение его центра: поле объекта сферической формы таково, как если бы вся его эффективная (то есть создающая гравиэффект, избыточная) масса была сосредоточена в центре, сведена в точку (здесь уместно вспомнить о ранее оговоренных допущениях при адаптации идеального закона Ньютона, где речь шла о взаимодействии материальных точек, к взаимодействию реальных масс (тел)).
Таким образом,
 gz=G
gz=G 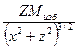
Исследуем это выражение и построим график gz по профилю, то есть вдоль линии наблюдения. Во-первых, отметим, что незавимимая переменная x в выражении gz стоит во второй степени – то есть кривая gz должна быть осесимметричной, а сама эта ось проходит через начало координат. Очевидно, что gz примет максимальное значение, когда абсцисса x=0, так как в этом случае знаменатель становится минимальным. Наконец, при стремлении x→∞, gz стремится к нулю. Эти соображения объясняют форму кривых gz, показанную на рисунке.
Мизб можно записать через произведение объема шара 4/3 πR3, где R его радиус, на избыточную (эффективную) плотность σ1 - σ0
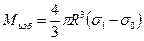
Выше уже говорилось, что геологические задачи – это обратные задачи, а не прямые. Поэтому далее необходимо обратиться непосредственно к решению обратных задач. Основной путь их решения связан с реализацией вышеизложенной идеи модельности, то есть опирается на так называемую схему подбора, когда на основании имеющихся представлений о строении разреза интерпретатор задается априорной моделью объекта и решает для этой модели прямую задачу. Затем расчетная кривая Δg сопоставляется с наблюденной и если требуемого соответствия не наблюдается, в модель вносятся определенные коррективы. После этого снова рассчитывается модельный гравиэффект, снова проводится сопоставление и так до тех пор, пока необходимая степень соответствия не будет достигнута. Тем самым устанавливаются итоговые значения М и Z, характеризующие объект поиска.
Таким образом видно, что процесс моделирования управляется петрофизическими и геометрическими параметрами модели – величинами σизб =σ1 - σ0 , а также Z0 – глубиной погружения центра шара и его радиусом R. Понятно, что определение этих двух величин исчерпывают возможности гравиразведки по решению геологической задачи. Ткое решение не является однозначным, поскольку одинковой массой M может обладать бесконечное множество шаров с одинаковым положением центра, но с различными R и σизб.. То есть можно говорить о проявлении так называемой теоретической эквивалентности при решении обратной задачи гравиразведки. Действительно, нетрудно убедиться из выражения для Мизб, что варьируя значениями R и σизб при условии, что Мизб не меняется, можно получить такое множество. Для того, чтобы выбрать из него единственный шар, отвечающий объективной реальности, необходимо иметь данные о плотностных характеристиках разреза. По кривой gz это сделать невозможно. Таким образом, для того, чтобы довести решение геологической задачи до конца, необходимо привлечь дополнительную к гравиразведочным данным информацию, то есть комплексировать гравиразведку с другими геофизическими методами или с бурением. О таком комплексировании можно прочитать в нашем учебном пособии [ 6 ]. Кроме моделирования, для решения обратной задачи используют метод характерных точек. Обычно это делается для того, чтобы оптимизировать параметры априорной ФГМ для реализации схемы подбора.
Приведем пример применения методики характерных точек в задаче об аномалии над шаром. Характерная точка здесь - это точка максимума на кривой gz . Если в выражении для gz принять x=0, то gz окажется равным G 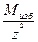 . Выберем теперь на оси абсцисс точку с координатой x1/2 , для которой gz равно половине от gzmax и составим уравнение
. Выберем теперь на оси абсцисс точку с координатой x1/2 , для которой gz равно половине от gzmax и составим уравнение
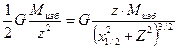
Решением этого уравнения можно получить значение Z, то есть координаты центра источника источника Z≈1,3 x1/2
Найдя Z можно найти и Мизб
Мизб= 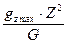
Мы рассмотрели пример решения обратной задачи для тела простой геометрической формы, но гораздо чаще приходится заниматься объектами сложной формы и непостоянной плотности. В этих случаях используются другие подходы, основанные на приближенных решениях численными методами – палеточными или копьютерными. С этими методами студенты ознакомятся на лабораторных и практических занятиях. Там же они смогут рассмотреть примеры применения гравиразведки при решении различных актуальных геологических задач - картирования солянокупольных структур, ископаемых рифов, рудных объектов и т.п.
Поскольку гравиразведка оказалась в нашем курсе первой из методов полевой геофизики, на ее примере были рассмотрены многие элементы практики геофизических работ, которые будут, как правило, опускаться в дальнейшем со ссылкой на имеющие место аналогии.
При составлении предложенного текста автор использовал без кавычек фрагменты из учебников В.В.Знаменского[1], а также В.К.Хмелевского [2] с соавторами, представленных в списке литературы. Сказанное в полной мере относится и к последующим разделам учебного пособия.
Лекция 6.
Магниторазведка.
Магниторазведка, как уже говорилось выше - это метод изучающий аномалии ΔТа в распределении естественного магнитного поля Земли, обусловленные различной способностью горных пород воспринимать намагничение, то есть намагничиваться и хранить это намагничение в течение многих геологических эпох.
Таким образом, основными физическими параметрами магниторазведки являются магнитная восприимчивость горных пород χ и их намагниченность J, связанные между собой соотношением 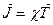 , где J – намагниченность, а Т – напряженность поля, измеряемые в А/м. Таким образом, χ есть величина относительная, безразмерная.
, где J – намагниченность, а Т – напряженность поля, измеряемые в А/м. Таким образом, χ есть величина относительная, безразмерная.
ΔТа представляет собой разность наблюденного и нормального значений поля
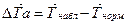
Под нормальным (или главным) полем понимается Тнорм = Т0 + Т, где сумма 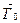 или Тдип – поле однородно намагниченной сферы (или магнитного диполя, помещенного в центр Земли и ориентированного примерно вдоль ее оси вращения) а
или Тдип – поле однородно намагниченной сферы (или магнитного диполя, помещенного в центр Земли и ориентированного примерно вдоль ее оси вращения) а 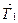 - это составляющая, связанная с особенностями внутреннего строения Земли, называемая материковой или континентальной аномалией.
- это составляющая, связанная с особенностями внутреннего строения Земли, называемая материковой или континентальной аномалией.
Вклад дипольной Тдип составляющей в наблюденное магнитное поле составляет примерно 70%, что объясняет такие его глобальные особенности, как увеличение напряженности поля в 2 раза при переходе от экватора к полюсу. Материковые аномалии 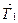 представляют собой плавноменяющиеся компоненты, образующие на Земле шесть крупных, соизмеряемых с площадью материков, положительных и отрицательных аномалий с амплитудой (0,1 -0,2) · 105нТл. Природа этих аномалий до конца неясна, но предполагается, что их источники располагаются на глубине ~3000км в области границы мантия - ядро Земли.
представляют собой плавноменяющиеся компоненты, образующие на Земле шесть крупных, соизмеряемых с площадью материков, положительных и отрицательных аномалий с амплитудой (0,1 -0,2) · 105нТл. Природа этих аномалий до конца неясна, но предполагается, что их источники располагаются на глубине ~3000км в области границы мантия - ядро Земли.
Дипольная составляющая может быть рассчитана теоретически, тогда как Т1 определяется только экспериментально. Таким образом, понятие нормального поля в магниторазведке существенно отличается от такового в гравиразведке. Однако, это далеко не единственная особенность магнитного поля.
Дата добавления: 2017-01-26; просмотров: 3440;











